COMPITI PER LE VACANZE 4A - GIUGNO 2015
!
!
MATEMATICA
!
Ripassare le proprietà e i grafici delle funzioni potenza, esponenziali, logaritmiche,
trigonometriche, trigonometriche inverse.
p.169 e ss. nn. 626, 630, 639, 640.
!
1)
Calcola il dominio della funzione:
2)
Calcola il dominio della funzione
[2≤x<5]
[-4≤x<
3)
∪
<x≤4]
Ricava per quali valori di x è positiva e per quali è negativa la funzione di equazione:
[ y > 0 se
; y < 0 se
]
4)
Risolvi la disequazione:
[0<x<
5)
Risolvi l’equazione: 3 +
[x= 0 ]
6)
Risolvi la disequazione:
7)
Risolvi la disequazione: log21/3 x + log9x > 0
8)
Rappresenta in uno stesso sistema di riferimento disegnato rappresenta il grafico di
ciascuna delle funzioni che seguono: A) y = 4-x B)
C)
D)
1)
È assegnata la funzione di equazione y = arcsen
[x≤
]
]
[0<x<
∨x>1]
. Per ciascuna delle affermazioni che
seguono decidi se è vera o falsa e giustifica la risposta che hai dato.
a)
Ha lo stesso codominio della funzione y = arcsenx
b)
Ha periodo π
c)
Ha periodo 4
d)
È simmetrica rispetto all’origine degli assi.
2)
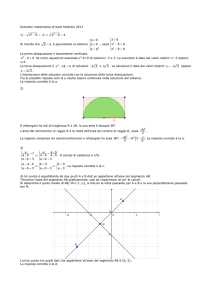
Sia ABC un triangolo equilatero inscritto in una circonferenza di raggio r. Indicato con P un
punto del minore dei due archi AC esprimere la somma delle distanze di P dai vertici del
triangolo. Rappresentare in [- π, π] funzione ottenuta, e mettere in evidenza il tratto di
grafico relativo al problema.
4)
[P
= x , y = 2senx +2
È assegnato un triangolo ABC di lati AB = 6a, AC = 2a, BC =
cosx ]
.
•
Calcolare cos
•
Indicato con M il punto medio di AB, risolvere il triangolo ACM e calcolare il raggio
della circonferenza circoscritta al triangolo CMB.
[ cos
; r=
.
]
!
[ - 2π/3 + 2kπ < x < 2π/3 + 2kπ ]
2)
5)
7sen2x – senx cosx ≥ 3
6)
senx + 1 ≤ 3cosx
7)
log2(3tg2x + 7) < 3
[ - π/2 + kπ ≤ x ≤ arctg(-3/4) + kπ ∨ π/4 + kπ ≤ x ≤ π/2 + kπ ]
[ - π/2 + 2kπ ≤ x ≤ 2artg(1/2) + 2kπ ]
Sono date due rette r, s tra loro parallele che hanno distanza 24a e una retta t che passa per
un punto A di r e forma un angolo di 60° con il piano delle rette r, s. È vero o falso che s e t
sono sghembe? Perché?
3)
Si dimostri che il volume del cilindro equilatero inscritto in una sfera di raggio r è medio
proporzionale fra il volume del cono equilatero inscritto e il volume della sfera. [2008 pni s.s.]
!
p. 579 nn. 1, 2, 3, 9, 10, 13, 14, 15, 18, 19, 20 (indicare dominio, codominio, simmetrie, monotonie,
disegnarne il grafico).
p. 580 n. 45, 46.
Ripassare cap. 14. P. 554 e ss. nn. 70, 74, 77, 80, 82, 84; p. 556 e ss. nn. 95, 96, 97,105, 109, 116.
!
!
FISICA
!
Ripassare i capitoli 18, 19, 20 (paragrafi1,2,3,4)
!
p. 922 e ss. nn. 7, 14, 15, 17, 18, 19, 28, 30.
!
!
Buone vacanze e e presto!