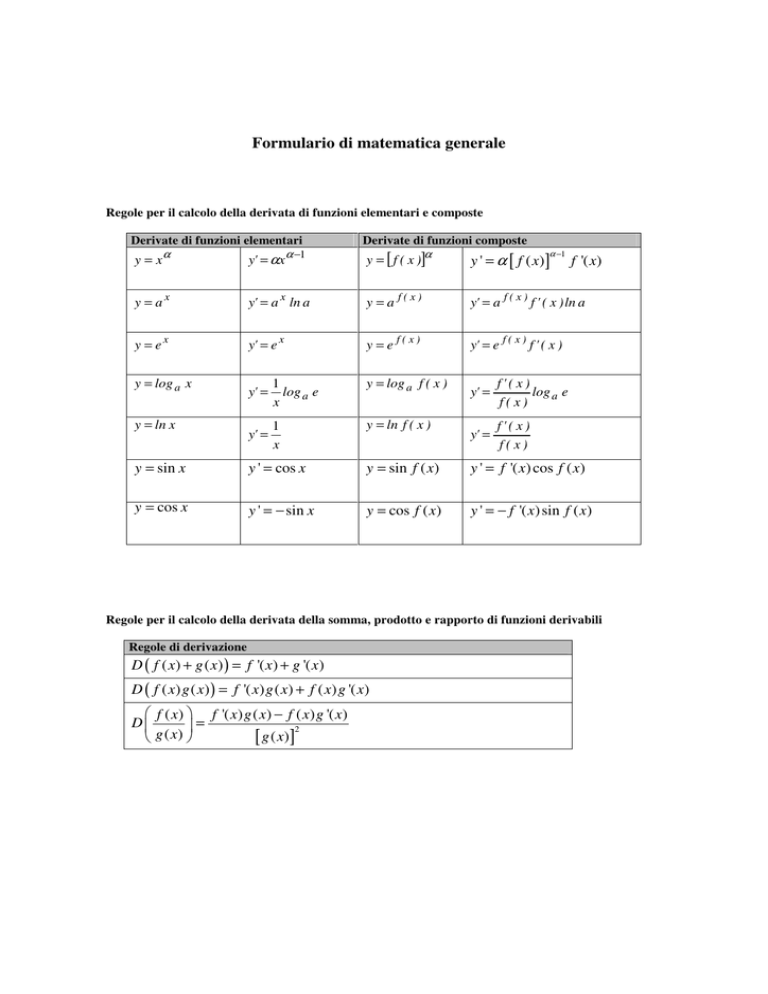
Formulario di matematica generale
Regole per il calcolo della derivata di funzioni elementari e composte
Derivate di funzioni elementari
y = xα
y' = αxα −1
Derivate di funzioni composte
α
y = [ f ( x )]
y ' = α [ f ( x)]
y = ax
y' = a x ln a
y =a f(x)
y' = a f ( x ) f ' ( x ) ln a
y = ex
y' = e x
y = e f(x)
y' = e f ( x ) f ' ( x )
y = log a x
y' =
1
log a e
x
y = log a f ( x )
y' =
f'( x)
log a e
f(x)
y' =
1
x
y = ln f ( x )
y' =
f'( x)
f(x)
y = ln x
α −1
f '( x)
y = sin x
y ' = cos x
y = sin f ( x)
y ' = f '( x) cos f ( x)
y = cos x
y ' = − sin x
y = cos f ( x)
y ' = − f '( x) sin f ( x)
Regole per il calcolo della derivata della somma, prodotto e rapporto di funzioni derivabili
Regole di derivazione
D ( f ( x) + g ( x) ) = f '( x) + g '( x)
D ( f ( x) g ( x) ) = f '( x) g ( x) + f ( x) g '( x)
f ( x) f '( x) g ( x) − f ( x) g '( x)
D
=
2
g ( x)
[ g ( x) ]
Regole per il calcolo dell’integrale indefinito di funzioni elementari e composte
Integrali indefiniti immediati
α ≠ −1,
∫
∫
1 α +1
xα dx =
x
+c
α +1
1
dx = ln x + c
x
ax
+c
ln a
Integrali indefiniti immediati per funzioni composte
α ≠ −1,
∫
α
∫ [ f ( x )]
f ' ( x )dx =
1
[ f ( x )]α +1 + c
α +1
f'( x)
dx = ln f ( x ) + c
f(x)
a f(x)
+c
ln a
∫
x
x
∫ e dx = e + c
∫
f(x)
f(x)
∫ e f ' ( x )dx = e + c
∫ sin x dx = − cos x + c
∫ sin f ( x) f '( x)dx = − cos f ( x) + c
∫ cos x dx = sin x + c
∫ cos f ( x) f '( x)dx = sin f ( x) + c
a x dx =
a f ( x ) f ' ( x )dx =
Regole di integrazione
Regola (o formula) di integrazione per parti
∫ f ( x )g' ( x )dx = f ( x )g( x ) − ∫ f ' ( x )g( x )dx
Regola (o formula) di integrazione per sostituzione
Posto x = g (t ) e dx = g '(t ) dt , risulta
∫ f ( x)dx = ∫ f ( g (t )) g '(t )dt












