DOCENTE: Vincenzo Pappalardo
MATERIA: Matematica
Integrali
indefini-
DEFINIZIONE DI
INTEGRALE INDEFINITO
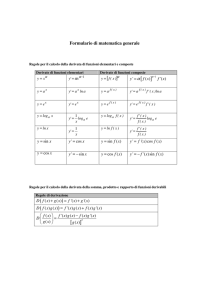
INTEGRALI INDEFINITI
IMMEDIATI
Infatti:
Riepilogo
L’INTEGRAZIONE
PER SOSTITUZIONE
In generale:
1. Sostituire la variabile d’integrazione x con un’altra
variabile t legata alla x dalla relazione x=g(t).
2. La funzione g(t) deve essere derivabile e invertibile
t=g-1(x).
3. Con queste condizioni la funzione integranda f(x)
diventa: f(x)=f[g(t)] e il differenziale dx diventa:
dx=g’(t)dt.
Formula dell’integrazione
per sostituzione
∫ f (x) = ∫ f [ g(t)]g'(t)dt
L’INTEGRAZIONE
PER PARTI
L’INTEGRAZIONE
DI FUNZIONI
RAZIONALI FRATTE
ESERCIZI
∫ f (x) = ∫ f [ g(t)]g'(t)dt