PROBLEMA 2
TRADIZIONALE
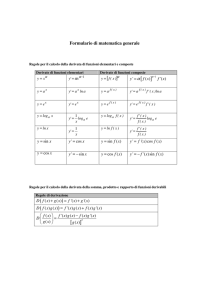
1.
Nel triangolo PAB rettangolo in B, se δ è l'angolo BPA, AB=PBtgδ :
ma δ é è uguale al coefficiente angolare della retta tangente che a
1
sua volta è la derivata prima x
Per cui essendo PB=x
calcolata nel punto P(x,lnx)
1
risulta AB=IPBtgδ I= ∣x . x ∣ =1 .
Anche nel caso di Gg AB rusulta costante perche la derivata prima
1
1
risulta x log a e e pertanto il prodotto x . x log a e = ∣log a e∣ .
2.
1
tgδ = x log a e ,nel caso δ =45° e x=1 risulta tg45°= log a e =1 cioè a=e;
1
analogamente tg135°= -1= log a e ,cioè a= e
3.
Essendo il punto P(1,e), l'area richiesta è l'area del rettangolo di lati 1 ed e a cui si sottrae
∫ lnx dx .Area = e-1
4
Per calcolare il volume richiesto conviene eseguire una tralazione in modo che l'asse di rotazione
coincida con l'asse y.La funzione diventa y=ln(x-1).Poichè la rotazione avviene attorno all'asse y
occorre calcolare la funzione inversa X=ey +1.
2
π ∫ e y 1 dy
a cui va sottratto π che il volume della cavità cilindrica
1 2
5
all'interno del solido considerato. Il risultato è π 2 e 2e− 2
Il volume si calcola