Il Monopolio e la Discriminazione di Prezzo
À L’impresa che opera in concorrenza perfetta non può fissare il prezzo
(price taker)
À Le imprese che godono di potere di monopolio godono di un margine di
discrezionalità nella fissazione
p
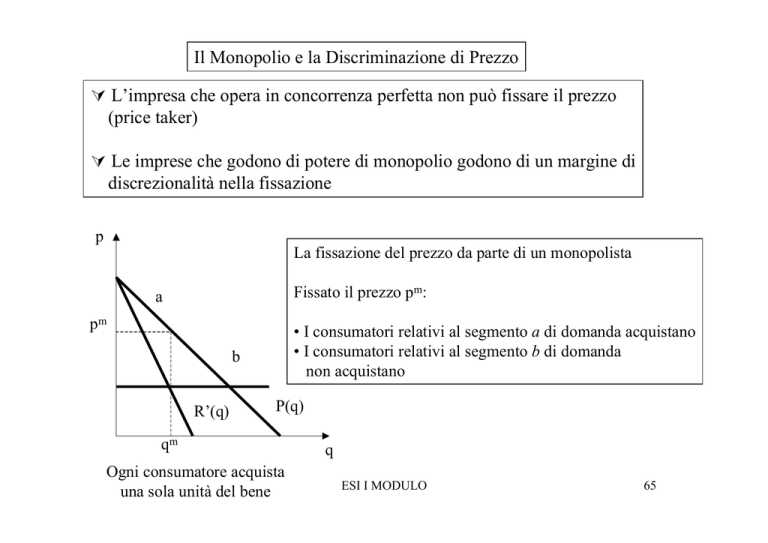
La fissazione del prezzo da parte di un monopolista
Fissato il prezzo pm:
a
pm
• I consumatori relativi al segmento a di domanda acquistano
• I consumatori relativi al segmento b di domanda
non acquistano
b
R’(q)
P(q)
qm
Ogni consumatore acquista
una sola unità del bene
q
ESI I MODULO
65
Il Monopolio e la Discriminazione di Prezzo
Problema del Monopolista: come raggiungere il segmento di mercato b
I soluzione: riduzione di prezzo.
• L’aumento del ricavo totale derivante dalla vendita di un numero maggiore
di unità ad un prezzo p<pm.
• La diminuzione del ricavo totale derivante dalla vendita dell’output complessivo
ad un prezzo più basso
II soluzione: prezzi non uniformi.
• Fissare un prezzo differente per ogni unità acquistata
DISCRIMINARE
Un produttore discrimina di prezzo quando due unità dello
stesso bene fisico sono vendute a prezzi
diversi allo stesso consumatore o a diversi consumatori
ESI I MODULO
66
Il Monopolio e la Discriminazione di Prezzo
•1. Tipologie di prezzi non uniformi
•2. Condizioni necessarie per discriminare
•3. Tipi di discriminazione
•4. Effetti sul benessere sociale
ESI I MODULO
67
Il Monopolio e la Discriminazione di Prezzo
•1. Tipologie di prezzi non uniformi
• Tariffa in due parti
• Sconti sulle quantità
•Vendita abbinata di due o più beni
ESI I MODULO
68
Il Monopolio e la Discriminazione di Prezzo
Tariffa in due parti
Il prezzo legato all’acquisto di un bene/servizio si compone di due parti:
• una componente fissa (premio) che il consumatore paga indipendentemente
dal consumo del bene/servizio
• una componente variabile legata alla quantità consumata del bene/servizio
ESI I MODULO
69
Il Monopolio e la Discriminazione di Prezzo
Tariffa in due parti.
Bene \ Servizio
Premio
Telefono, Gas, Elettricità Canone
Taxi
Tariffa iniziale
Circolo Sportivo
Quota Iscrizione
ESI I MODULO
Tariffa
variabile
n. unità
consumate
Distanza
percorsa
Accesso alle
strutture
70
Il Monopolio e la Discriminazione di Prezzo
Sconti sulle quantità.
Il prezzo del bene/servizio varia con il numero di unità del bene acquistate dal cliente
(utilità marginale decrescente): buoni sconto, tariffe elettriche.
Vendita abbinata (collegata) di due o più beni.
Il consumatore può acquistare il bene/servizio se e solo se acquista un altro bene:
acquisto di un bene durevole più i servizi di assistenza, acquisto macchina Polaroid
e relativa pellicola, acquisto fotocopiatrice e carta della stessa marca fotocopiatrice.
ESI I MODULO
71
Il Monopolio e la Discriminazione di Prezzo
2. Condizioni necessarie per discriminare
Condizioni necessarie per discriminare
•a. Potere di monopolio
•b. Conoscere le disponibilità a pagare dei consumatori i.e.
conoscere i prezzi di riserva dei consumatori
•c. Impedire l’arbitraggio
ESI I MODULO
72
Il Monopolio e la Discriminazione di Prezzo
c. Impedire l’arbitraggio: evitare che i consumatori che hanno acquistato il bene
ad un prezzo più basso lo rivendano a coloro che sono disposti a pagare un prezzo
più alto.
Caratteristiche merceologiche
Garanzie
Adulterazione del prodotto
Clausole Contrattuali
Integrazione Verticale
ESI I MODULO
73
3. Tipi di discriminazione
Il Monopolio e la Discriminazione di Prezzo
Discriminazione di primo grado o perfetta.
Il produttore conosce esattamente la curva di domanda di ogni consumatore e
conseguentemente si appropria di tutto il suo surplus
Discriminazione di secondo grado
Il produttore non riesce ad appropriarsi in modo completo del surplus del
consumatore. Il produttore non conosce le caratteristiche della funzione di
domanda dei consumatori. L’appropriazione parziale del surplus avviene
mediante meccanismi di autoselezione.
Discriminazione di terzo grado.
Il produttore non riesce ad appropriarsi in modo completo del surplus del
consumatore. Il produttore conosce alcune caratteristiche della funzione di
domanda dei consumatori. L’appropriazione parziale del surplus avviene
sfruttando le caratteristiche note.
ESI I MODULO
74
DL: Perdita Secca
Discriminazione di prezzo di primo grado o perfetta
CS: Surplus del Consumatore
R: Rendita
p(q): Domanda singolo consumatore
p
pm
p
R’
p(q)
p(q)
C’
pc
C’
R’
qm
q
q
qc
pm , qm
T mD = CSc + pcqc ; qc
πm = pmqm - c(qm )
πmD = pc qc - c(qc ) + CSc = W c > W m > πm
W m = πm + CSm
ESI I MODULO
75
Discriminazione di prezzo di primo grado o perfetta
Q(p): Domanda complessiva di n consumatori caratterizzati da identica funzione di
domanda
Tariffa pagata da ogni consumatore
T
mD
CSc (Qc )
=
+
n
Qc
p
;
n
c
ESI I MODULO
76
Il produttore conosce alcune caratteristiche della funzione di
domanda dei consumatori. Ad esempio un produttore divide
la domanda dei consumatori per classi di età. Le classi di età
sono individuate in modo tale che le domande ad esse associate
siano indipendenti
{ p1 , p2 ,..., pn }
n
{q1 , q2 ,..., qn } ⇒ Q = ∑ qi
i =1
da cui
n
π = ∑ pi qi − C (Q )
i =1
imponendo la c.p.o sul mercato i - mo
pi − C '
1
∂π
= 0 ⇒ Li =
=
∂pi
pi
ηi
ESI I MODULO
77
Tariffa volo New York – Los Angeles
Prima Classe
Economica Ordinaria
Turistica
Elasticità Domanda trasporto passeggeri
Prima Classe
Economica Ordinaria
Turistica
Costo
2000
1200
500
prezzo
0.3
0.4
0.9
reddito
1.2
1.2
1.8
Fonte: New York Times 1987.
ESI I MODULO
78
Margine di contribuzione relativo (%) per differenti modelli di auto in Europa
Modello
Belgio Francia Germania Italia Gran bretagna
Fiat Uno
7.6
8.7
9.8
21.7
8.7
Nissan Micra
8.1
23.1
8.9
36.1
12.5
Ford Escort
8.5
9.5
8.9
8.9
11.5
Peugeot 405
9.9
13.4
10.2
9.9
11.6
Mercedes 190 14.3
14.4
17.2
15.6
13.2
(Note: prezzi prima delle tasse)
Fonte: Verboven F. International Price Discrimination in the European Car Market.
Rand Journal of Economics (1996).
ESI I MODULO
79
Discriminazione di terzo grado vs prezzo uniforme
n
Q = ∑ qi
i =1
Prezzo Uniforme
C (Q ) = cQ
π = ( p − c )Q( p )
cpo
n ∂q
n
∂π
i
= ( p − c )∑
+ ∑ qi = 0
∂p
i =1 ∂p i =1
da cui
n
n
Lp =
p−c
=−
p
ESI I MODULO
∑ qi
i =1
n ∂q
i
p∑
i =1 ∂p
=
∑ qi
i =1
n
(1)
∑ qi ηi
i =1
80
Invertendo la (1) è immediato ottenere
n
∑ qi ηi
1 i =1
= n
Lp
∑ qi
i =1
da cui segue
ηmin <
1
1
1
< ηmax ⇒
< Lp <
Lp
ηmax
ηmin
I consumatori nei mercati con bassa elasticità sono danneggiati dalla
discriminazione e preferirebbero un prezzo uniforme.
I consumatori in mercati molto elastici preferiscono la discriminazione
ESI I MODULO
81
Variaz. complessiva di benessere
Discriminazione di prezzo di terzo grado
Monopolio Discriminate
qi = D( pi );
i = 1,..., n
n
π = ∑ ( pi − c )qi (1)
i =1
Siano
pim
qim
e
i = 1,..., n
le quantità ottime, allora il surplus del consumatore (CSmD), la rendita del
produttore (RPmD) e il benessere sociale (WmD) nel caso di discriminazione
sono dati da:
CS
mD
( )
n
= ∑ CSi pim
i =1
RP
mD
n
(
( )
CSi pim = ∫p m Di ( pi )dpi
i
p*
i = 1,..., n
)
= ∑ pim − c qim
i =1
W mD = RP mD + CS mD
(2)
ESI I MODULO
82
Discriminazione di prezzo di terzo grado
Monopolio Discriminate
qi = D( p );
i = 1,..., n
n
π = ∑ ( p − c )qi
(3)
i =1
Siano
pm
e
qim
i = 1,..., n
le quantità ottime, allora il surplus del consumatore, (CSmU),
la rendita del produttore (RPmU) e il benessere sociale (WmU)
nel caso di prezzo uniforme sono dati da:
CS
mU
( )
n
= ∑ CS i p m
i =1
n
(
( )
CS i p m = ∫p Di ( p )dp
p*
m
i = 1,..., n
i
)
RP mU = ∑ p m − c qim
i =1
mU
W mU = RP
+ CS mU
(4)
ESI I MODULO
83
Discriminazione di prezzo di terzo grado
La Variazione Complessiva del Benessere
∆W = W mD − W mU =
n
=∑
i =1
[ ( ) − CS ( p )]+ ∑ [( p
CSi pim
i
m
n
i =1
m
i
)
(
) ]
− c qim − p m − c qim
(5)
La relazione (5) ammette un Upper e un Lower Bound. Per dimostrare ciò
si considerino le seguenti relazioni:
'
CS =
∂CS
= − D( p ) < 0
∂p
∂D( p )
>0
CS '' = −
∂p
(6)
ESI I MODULO
84
Discriminazione di prezzo di terzo grado
Le relazioni (6) implicano la convessità della funzione CS rispetto al prezzo p
Individuazione del UB
CSi ( pi )
p m < pim
( )
CSi p m
( )
CSi p im
pm
p im
pi
ESI I MODULO
85
Discriminazione di prezzo di terzo grado
Individuazione del UB
CSi( pi m ) − CSi( p m )
p m − pi m
≤ −CS i ' ( pi m ) = Di( pi m )
(7)
da cui segue
CSi( pi m ) − CSi( p m ) ≤ Di( pi m )( p m − pi m )
Dalla (5) e dalla (7) è immediato ottenere
n
∆W ≤ ∑ Di( pi )( p m − pi
m
i =1
(
)
n
m
m
= p m − c ∑ qi − qi
i =1
m
n
(
)
(
)
m
m
m
=
) + ∑ pi − c qi − p m − c qi
i =1
∆qi = qim − qim < 0
ESI I MODULO
86
Discriminazione di prezzo di terzo grado
Individuazione del LB
CSi ( pi )
( )
CSi p im
p m > pim
( )
CSi p m
pim
pm
pi
ESI I MODULO
87
Discriminazione di prezzo di terzo grado
Individuazione del LB
CSi( pi m ) − CSi( p m )
m
pi − p m
≥ CS i ' ( p m ) = − Di ( p m )
(9)
da cui segue
CSi( pi m ) − CSi( p m ) ≥ − Di ( p m )( pi m − p m )
Dalla (5) e dalla (9) è immediato ottenere
n
∆W ≥ ∑ − Di ( p m )( pi
n
(
i =1
= ∑ pi
i =1
m
)
m
n
(
)
(
)
m
m
m
− p m ) + ∑ pi − c qi − p m − c qi =
i =1
m
m
− c qi − qi
∆qi = qim − qim > 0
ESI I MODULO
88
Discriminazione di prezzo di terzo grado
Dalla (8) e dalla (10) segue
∑(
n
i =1
pim
)
(
)
n
− c ∆qi ≤ ∆W ≤ p − c ∑ ∆qi
m
(11)
i =1
• Se
n
∑p
n
m
i =1
= p<
n
∑ pim
i =1
n
n
⇒∑
i =1
qim
n
>∑
i =1
qim
n
⇒∑ ∆qi < 0
(12)
i =1
• Se
n
∑p
i =1
n
n
m
= p>
∑ pim
i =1
n
n
⇒∑
i =1
qim
n
<∑
i =1
qim
n
⇒∑ ∆qi > 0
(13)
i =1
ESI I MODULO
89
Discriminazione di prezzo di terzo grado
n
∑p
i =1
= p<
n
n
∑p
i =1
n
n
m
∑ pim
i =1
n
n
⇒∑
i =1
qim
n
>∑
i =1
qim
n
⇒∑ ∆qi < 0
(12)
i =1
n
m
= p>
∑ pim
i =1
n
n
⇒∑
i =1
qim
n
<∑
i =1
qim
n
⇒∑ ∆qi > 0
(13)
i =1
Dalle relazioni (12) e (13) è immediato ricavare che:
La discriminazione di prezzo riduce il benessere se non aumenta la produzione totale
ESI I MODULO
90
Discriminazione di prezzo di terzo grado
Alcune tipologie di discriminazione di prezzo di terzo grado
Basing Point Price (Prezzo del Punto Base)
• Fissare prezzi differenti in funzione della distanza dal sito produttivo
Sistema utilizzato dall’industria dell’acciaio americano fra il 1901-1948
Caratteristiche Industria:
•1. Numero imprese (rispetto altre industrie): medio
•2. Grado di concentrazione: R4 =60%
•3. Differenziazione produttiva bassa
•4. Elasticità domanda bassa
•5. Ordini su grandi lotti
•6. Tasso progresso tecnologico basso
ESI I MODULO
91
Discriminazione di prezzo di terzo grado
Il Basing Point Price nell’industria dell’acciaio americano fra il 1901-1948
Prezzo
di mercato
$
47.6 $
40 $
Pittsburg
40 $: prezzo di una t
di acciaio a Pitts.
7.6 $: prezzo di trasporto
di una t di acciaio da
Pitts. a Chic.
Prezzo del Punto Base:
47.6 $
Chicago
località
Punto Base
ESI I MODULO
92
Fissando il prezzo di una t di acciaio a 47.6 nell’industria, le aziende che vi operano
ottengono:
• Un guadagno derivante dalla differenza fra il prezzo alla produzione (40 $)
e il prezzo praticato in tutta l’industria (47.6 $) che tiene conto della
distanza fra la località scelta come punto base e il sito produttivo più lontano
• Un meccanismo che garantisce l’affermarsi di accordi collusivi
Mercato servito da Pittsburg
47.6 $
Mercato servito da Chicago
40 $
Pittsburg
Punto Base
Chicago
Consumatore
Indifferente
ESI I MODULO
località
93
Discriminazione di prezzo di terzo grado
Controlli verticali come strumento discriminatorio
M
p1*
L1 =
p*2
c
p1 − c 1
= ⇒ p1* =
p1
ε1
1 − (1 / ε1 )
p2 − c 1
c
*
L2 =
= ⇒ p2 =
p2
ε2
1 − (1 / ε 2 )
1
2
ε1
p*2 < p1*
ε2.
Il monopolista, M, produce un solo bene utilizzato da due settori, 1 e 2, caratterizzati da
differenti elasticità ε1 e ε2 (ε2 > ε1).
Per Hp le imprese nei due settori hanno costi nulli e il bene prodotto in un settore
può essere impiegato come input nell’altro settore. Il monopolista sostiene un costo marginale
pari a c
ESI I MODULO
94
Controlli verticali come strumento discriminatorio
Il Monopolista per discriminare deve vendere ad un prezzo p1 nel mercato 1 e a un prezzo p2
nel mercato 2 (p2< p1).
Tuttavia le imprese del settore 1 acquisteranno dal settore 2 (arbitraggio)
Soluzione.
• Il monopolista a monte si integra a valle
con una azienda del settore 2
• Fissa il prezzo finale di questa impresa a p2
• Vende a tutte le altre imprese nel settore 2
il bene da lui prodotto a p1
M
p1*
p1*
1
2
ε1
ε2.
p2*
Il caso.
Negli USA l’ALCOA negli anni 50 aveva potere
di monopolio nella produzione dei lingotti di
alluminio vergine, un bene intermedio: l’ALCOA
si integrò in mercati con forte elasticità della
domanda (fogli di alluminio) e, attraverso la sua
politica di determinazione del prezzo del bene
intermedio, ha eliminato la concorrenza a valle.
ESI I MODULO
95
Discriminazione di prezzo di secondo grado
Il produttore non conosce le caratteristiche della funzione di
domanda dei consumatori. L’appropriazione parziale del surplus avviene
mediante meccanismi di autoselezione.
p
p
p*
Funzione di domanda
non nota
p**
1
p’ CS
p’
q’
q
CS2
q’’
Consumatore 1
q
Consumatore 2
ESI I MODULO
96
Discriminazione di prezzo di secondo grado
La soluzione migliore per il monopolista è rappresentata dalla fissazione di
una tariffa in due parti (T): T=F+pq.
Ma ciò fa nascere due ordini di problemi
• Come fissare il premio (F).
• Come fissare la parte variabile (p).
ESI I MODULO
97
p
p
p*
p’
p**
CS1
p’
q’
q
CS2
q’’
Consumatore 1
q
Consumatore 2
Il monopolista sceglie una sola tariffa in due parti:
• può fissare una tariffa ove il premio fisso è CS2 e il prezzo e p’
• può fissare una tariffa ove il premio fisso è CS1 e il prezzo e p’
ESI I MODULO
98
Individuazione della tariffa ottima
Discriminazione di prezzo di secondo grado
Sia:
θiV (qi ) − T se paga T e consuma qi unità
U i (qi ) =
i : 1,2 (1)
se non acquista
0
La funzione di utilità del generico consumatore i, dove:
θi : parametro che esprime la preferenza ( θ1 < θ 2 )
1 − (1 − qi ) 2
; qi ∈ [0,1] ⇒ U ' (qi ) > 0, U '' (qi ) < 0
V (qi ) =
2
T = F + pqi ; tariffa in due parti
La funzione di domanda del generico consumatore è ottenibile derivando la (1)
rispetto a qi:
1 − (1 − qi )2
max U i (qi ) = max θi
− F − pqi (2)
qi
qi
2
ESI I MODULO
99
Derivando rispetto a qi la (2) è immediato ricavare la funzione di domanda
di ogni consumatore:
qi = 1 −
p
θi
i : 1,2
(3)
Quindi il CS del generico consumatore i è dato da:
(θi − p )2
p
CSi ( p ) = (θi − p )1 − = 0.5
θi
θi
(4)
Se λ ∈ [0,1] rappresenta la frazione dei consumatori con preferenza θ1
allora la domanda di mercato è data da
λ 1− λ
p
Q = λq1 + (1 − λ )q2 = 1 − +
p = 1µ
θ1 θ 2
(5)
Dove
1 λ 1− λ
= +
µ θ1 θ 2
(6)
ESI I MODULO
100
La determinazione della tariffa F
Essendo per la (4):
CS1 ( p ) < CS 2 ( p )
(7)
Allora:
0.5(θ1 − p )
F = CS1 ( p ) =
θ1
2
(8)
Sia c< θ1 < θ2 allora la funzione di profitto del monopolista è pari a
0.5(θ1 − p )
p
Max CS1 ( p ) + ( p − c )Q =
+ ( p − c )1 −
p
θ1
µ
2
(9)
Derivando la (9) rispetto a p e risolvendo è immediato ottenere il prezzo ottimo:
pD =
θ1c
c
=
2θ1 − µ 2 − µ θ1
(10)
ESI I MODULO
101
Considerazioni
Se il monopolista fissasse un prezzo uniforme la funzione di domanda è data da:
Q = 1−
p
µ
(11)
Il profitto è data da:
p
π = ( p − c )Q = ( p − c )1 −
µ
(12)
Essendo:
c+µ
p =
> pD
2
U
(13)
e
(θ1 − p )
∂F ∂CS1 ( p )
=
=−
<0
∂p
∂p
θ1
Allora la perdita di profitto causata dalla riduzione di prezzo è
compensata dall’aumento del premio
ESI I MODULO
102
Considerazioni
Il profitto conseguito dal monopolista è sicuramente inferiore a quello ottenuto
mediante l’utilizzo di una tariffa in due parti nel caso in cui le preferenze dei
consumatori siano note.
Il monopolista può effettuare una discriminazione di terzo grado e
conseguire un profitto più elevato di quello ottenuto attraverso una sola
tariffa in due parti.
Tuttavia il monopolista per discriminare di primo grado o di terzo grado
deve avere molte più informazioni sulla domanda di ogni consumatore
Imporre a consumatori distinti tariffe diverse per l’acquisto dello stesso
bene potrebbe essere vietato.
ESI I MODULO
103
Tariffe in due parti doppie
Il monopolista offre più di un profilo tariffario per estrarre il surplus del consumatore
Sia:
θiV (qi ) − Ti se paga Ti e consuma qi unità
U i (qi ) =
i : 1,2 (1)
se non acquista
0
La funzione di utilità del generico consumatore i, dove:
θi : parametro che esprime la preferenza (θ1 <θ 2 )
1 − (1 − qi ) 2
; qi ∈ [0,1] ⇒ U ' (qi ) > 0, U '' (qi ) < 0
V (qi ) =
2
Ti = Fi + pqi ; tariffa in due parti
ESI I MODULO
104
Tariffe in due parti doppie
La funzione obiettivo del monopolista è data da:
Π m = λ(T1 − cq1 ) + (1 − λ )(T2 − cq2 )
(2)
Vincoli:
θ1V (q1 ) − T1 ≥ 0
(3a)
θ 2V (q2 ) − T2 ≥ θ2V (q1 ) − T1
(3b)
Per quanto mostrato nel caso di una sola tariffa doppia la scelta ottima del
monopolista è rappresentata dal fissare:
T1 = θ1V (q1 )
(4)
Da cui segue per la (3b):
T2 = θ 2V (q2 ) − (θ 2 − θ1 )V (q1 )
ESI I MODULO
(5)
105
Tenendo conto della (4) e della (5) la (2) può essere scritta come
( ( )
( )
max Π m = λ(θ1V (q1 ) − cq1 ) + (1 − λ ) θ 2V q2 − (θ 2 − θ1 )V q1 − cq2
q1 , q2
)
Derivando la (6) rispetto a q1
∂Π m
= 0 ⇒ λθ1V ' (q1 ) − (1 − λ )θ 2V ' (q1 ) + (1 − λ )θ1V ' (q1 ) - λc = 0
∂q1
La precedente può essere scritta come
1 (1 − λ ) θ 2
θ
=c
θ1V ' (q1 )1 − (1 − λ ) 2 = λc ⇒ θ1V ' (q1 ) −
θ1
λ θ1
λ
Da cui segue
θ1V ' (q1 ) =
c
(1 − λ ) θ 2 − θ1
1 − λ
θ
1
(7)
ESI I MODULO
106
(6)
Derivando la (6) rispetto a q2
∂Π m
= c ⇒ λθ 2V ' (q2 ) = c
∂q2
Considerazioni
Il consumatore con preferenza θ1 non acquista se
θ1V ' (q1 ) < 0
ovvero
1−
se
(1 − λ ) θ2 − θ1
λ
θ1
θ 2 − θ1
<0⇒λ<
θ2
ESI I MODULO
107
Nel caso in cui entrambi i consumatori sono serviti allora è immediato osservare
U ' (q1 ) = θ1V ' (q1 ) =
c
>c
(1 − λ ) θ 2 − θ1
1 − λ
θ
1
U ' (q2 ) = θ 2V ' (q2 ) = c
I consumatori che hanno prezzi di riserva più bassi consumano una quantità minore
rispetto a quella ottimale
T1 = θ1V (q1 )
(4)
T2 = θ 2V (q2 ) − (θ 2 − θ1 )V (q1 )
ESI I MODULO
(5)
108
Composizione delle tariffe in due parti
S
p
e
s
a
T1
S
p
e
s
a
T2
q
q
ESI I MODULO
109
Esempio
Nel 1996 il mercato della telefonia mobile inglese era caratterizzato da quattro
operatori:Vodaphone, Cellnet, Orange e One2One. La One2One nell’ottobre
dello stesso anno presento i seguenti schemi tariffari
Canone Mensile
Costo per scatto nel Week-end
One2One Bronze
£ 17.50
29p
One2OneGold
£ 36
18p
Fonte. Cabral L.M. B. Introduction to Industrial Organization. MIT Press. 2000
ESI I MODULO
110
Vendite Collegate
Una vendita collegata di due o più beni è una vendita in cui un consumatore può
acquistare un prodotto solo se ne acquista anche un altro
• Vendita a pacchetto: due o più prodotti venduti solo in proporzioni fisse
• Vendita abbinata vincolata: acquisto di un bene base consumato in quantità fissa
(una unità) e un bene complementare consumato in quantità variabili
ESI I MODULO
111
Vendita a pacchetto: due o più prodotti venduti solo in proporzioni fisse
Il prezzo di Microsoft Office negli USA nel 1993 era di 750$. Il
prodotto comprendeva le seguenti applicazioni il cui prezzo unitario di
vendita è riportato di fianco:
Excel
Word
Powerpoint
Access
Microsoft Mail
495$
495$
495$
495$
80$
Se le applicazioni fossero state vendute separatamente il ricavo conseguito
dalla Microsoft sarebbe stato di 2060$.
Fonte. Cabral L.M. B. Introduction to Industrial Organization. MIT Press. 2000
ESI I MODULO
112
Vendita a pacchetto: due o più prodotti venduti solo in proporzioni fisse
No. Users
Writer
Number Cruncher
Generalist
40
40
20
Prezzo di Riserva
Word
Spreadsheet
Processor
50
0
0
50
30
30
Le possibili strategie di massimizzazione dei ricavi
1. Vendita separata delle applicazioni ad un prezzo di 50
(RTWord Processor=2000, RTSpreadsheet =2000, RTTotale =4000 )
2. Vendita separata delle applicazioni ad un prezzo di 30
(RTWord Processor =1800, RTSpreadsheet =1800, RTTotale =3600)
3. Offrire oltre allo schema di prezzo 1. la possibilità di acquistare
entrambe le applicazioni al prezzo di 60
(RTWord Processor=2000, RTSpreadsheet =2000, RTTotale =4000 ) (1.)
+
(3.)
(RTWord Processor+Spreadsheet =1200)
Fonte. Cabral L.M. B. Introduction to Industrial Organization. MIT Press. 2000
ESI I MODULO
113












