PARABOLA

PARABOLA
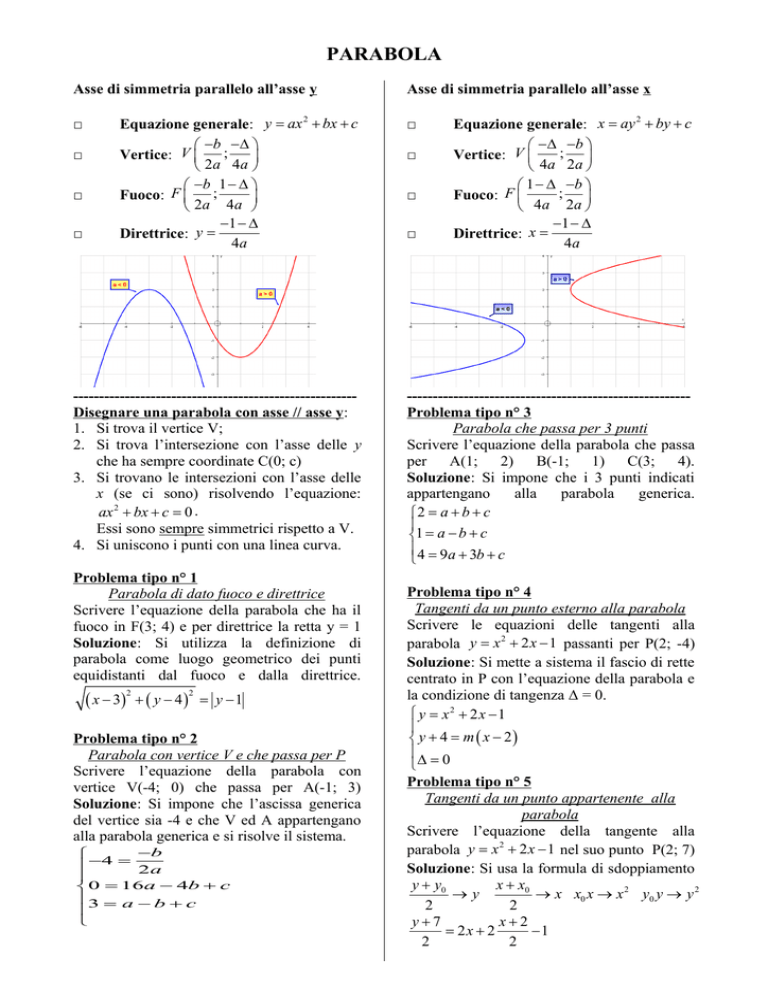
Asse di simmetria parallelo all’asse y
Asse di simmetria parallelo all’asse x
□
□
□
□
□
Equazione generale: y = ax 2 + bx + c
æ -b -D ö
;
Vertice: V ç
÷
è 2a 4a ø
æ -b 1 - D ö
;
Fuoco: F ç
÷
è 2a 4a ø
-1 - D
Direttrice: y =
4a
------------------------------------------------------Disegnare una parabola con asse // asse y:
1. Si trova il vertice V;
2. Si trova l’intersezione con l’asse delle y
che ha sempre coordinate C(0; c)
3. Si trovano le intersezioni con l’asse delle
x (se ci sono) risolvendo l’equazione:
ax 2 + bx + c = 0 .
Essi sono sempre simmetrici rispetto a V.
4. Si uniscono i punti con una linea curva.
Problema tipo n° 1
Parabola di dato fuoco e direttrice
Scrivere l’equazione della parabola che ha il
fuoco in F(3; 4) e per direttrice la retta y = 1
Soluzione: Si utilizza la definizione di
parabola come luogo geometrico dei punti
equidistanti dal fuoco e dalla direttrice.
( x - 3) + ( y - 4 )
2
2
= y -1
Problema tipo n° 2
Parabola con vertice V e che passa per P
Scrivere l’equazione della parabola con
vertice V(-4; 0) che passa per A(-1; 3)
Soluzione: Si impone che l’ascissa generica
del vertice sia -4 e che V ed A appartengano
alla parabola generica e si risolve il sistema.
-b
ì
ï -4 = 2a
ï
í0 = 16a - 4b + c
ï3 = a - b + c
ï
î
□
□
□
Equazione generale: x = ay 2 + by + c
æ -D -b ö
; ÷
Vertice: V ç
è 4a 2a ø
æ 1 - D -b ö
; ÷
Fuoco: F ç
è 4a 2a ø
-1 - D
Direttrice: x =
4a
------------------------------------------------------Problema tipo n° 3
Parabola che passa per 3 punti
Scrivere l’equazione della parabola che passa
per A(1; 2) B(-1; 1) C(3; 4).
Soluzione: Si impone che i 3 punti indicati
appartengano
alla
parabola
generica.
ì2 = a + b + c
ï
í1 = a - b + c
ï 4 = 9a + 3b + c
î
Problema tipo n° 4
Tangenti da un punto esterno alla parabola
Scrivere le equazioni delle tangenti alla
parabola y = x 2 + 2 x - 1 passanti per P(2; -4)
Soluzione: Si mette a sistema il fascio di rette
centrato in P con l’equazione della parabola e
la condizione di tangenza Δ = 0.
ì y = x2 + 2x -1
ï
í y + 4 = m ( x - 2)
ïD = 0
î
Problema tipo n° 5
Tangenti da un punto appartenente alla
parabola
Scrivere l’equazione della tangente alla
parabola y = x 2 + 2 x - 1 nel suo punto P(2; 7)
Soluzione: Si usa la formula di sdoppiamento
y + y0
x + x0
®y
® x x0 x ® x 2 y0 y ® y 2
2
2
y+7
x+2
= 2x + 2
-1
2
2
CIRCONFERENZA
Ogni circonferenza del piano cartesiano può essere descritta dall’equazione di 2° grado:
x 2 + y 2 + ax + by + c = 0 o in modo equivalente da:
( x - x0 )
2
+ ( y - y0 ) = r 2
2
2
2
æ a bö
a
b
Centro C ç - ; - ÷ e Raggio r = æç - ö÷ + æç - ö÷ - c .
è 2 2ø
è 2ø è 2ø
Problema tipo n° 1 Circonferenza di dato centro e raggio
Scrivere l’equazione della circonferenza di centro O(2; -1) e raggio r = 3.
Soluzione: Si utilizza la definizione di circonferenza come luogo geometrico dei punti del piano
equidistanti dal centro.
2
2
( x - 2 ) + ( y + 1) = 32
Problema tipo n° 2 Circonferenza di dato centro e passante per un punto
Scrivere l’equazione della circonferenza di centro O(1; 3) e passante per il punto P(2; 5)
Soluzione: Si calcola il raggio della circonferenza con la formula della distanza fra due punti e ci si
riconduce al problema n° 1.
2
2
2
2
r 2 = ( 2 - 1) + ( 5 - 3) = 5 ==> ( x - 1) + ( y - 3) = 5
Problema tipo n° 3 Circonferenza di dato diametro di estremi A e B
Scrivere l’equazione della circonferenza il cui diametro è dato dal segmento di estremi A(0;2) e
B(4; -6).
Soluzione: Si calcola il centro della circonferenza come punto medio del segmento AB ed il raggio
dividendo a metà la distanza AB.
æ 0+4 2-6ö 2
2
2
2
2
Cç
;
÷ r = ( 0 - 4 ) + ( 2 + 6 ) = 80 ==> ( x - 2 ) + ( y + 2 ) = 80
2 ø
è 2
Problema tipo n° 4 Circonferenza passante per 3 punti non allineati
Scrivere l’equazione della circonferenza passante per i punti A(1; 0) B(-1; 2) C(3; -3)
Soluzione (a): si impone che i 3 punti appartengano alla circonferenza.
ì1 + a + c = 0
ï
í1 + 4 - a + 2b + c = 0
ï9 + 9 + 3a - 3b + c = 0
î
Soluzione (b): si trovano due assi di due segmenti diversi (per es. AB e AC), si intersecano e si
trova il circocentro; la distanza di un punto qualunque dal circocentro è il raggio della circonferenza
Problema tipo n° 5 Circonferenza di dato centro e tangente ad una retta
Scrivere l’equazione della circonferenza di centro C(3; 2) e tangente alla retta x + y - 1 = 0
Soluzione: Si calcola il raggio della circonferenza come la distanza del centro dalla retta.
3 + 2 -1
2
2
r=
= 2 2 ==> ( x - 3) + ( y - 2 ) = 8
1+1
Problema tipo n° 6 Tracciare le tangenti da un punto esterno alla circonferenza
Scrivere l’equazione della tangenti alla circonferenza x 2 + y 2 - 2 x = 0 passanti per P(9/4; 0)
Soluzione: Si scrive il fascio di rette centrato in P. Si calcola il raggio della circonferenza e lo si
uguaglia alla distanza del centro della circonferenza dalla retta generica per P.
4m - 9m
9ö
4
æ
y - 0 = m ç x - ÷ => 4mx - 4 y - 9m = 0 ; C(1; 0) r = 1 1 =
m
=
±
=>
4ø
3
è
16m 2 + 16