x - Macroarea di Scienze

Calcolo differenziale
dove a,b,c,d sono valori costanti fissati.
y può essere definita per ogni valore di x.
Es: x=1 => y(1)=a+b+c+d ;
x=2 => y(2)=8a+4b+2c+d; …
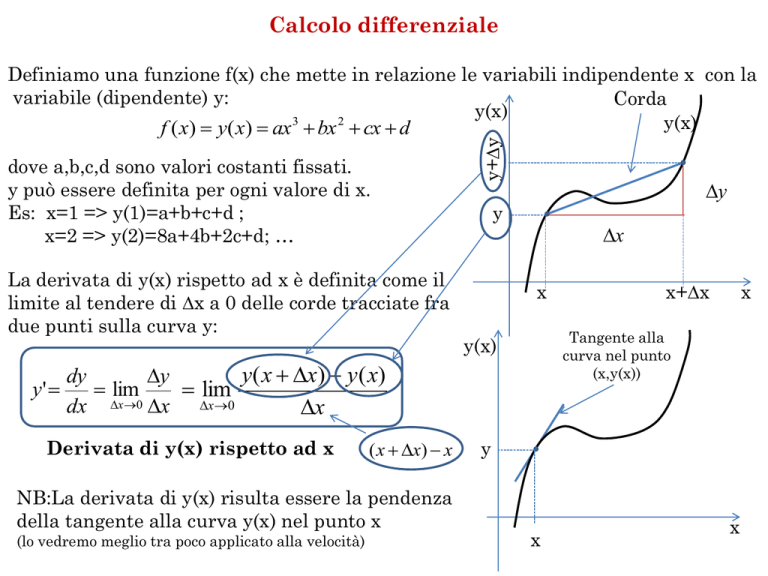
La derivata di y(x) rispetto ad x è definita come il
limite al tendere di x a 0 delle corde tracciate fra
due punti sulla curva y:
y' 
y+y
Definiamo una funzione f(x) che mette in relazione le variabili indipendente x con la
variabile (dipendente) y:
Corda
y(x)
y(x)
f ( x)  y( x)  ax3  bx 2  cx  d
y
y
x
x
( x  x)  x
NB:La derivata di y(x) risulta essere la pendenza
della tangente alla curva y(x) nel punto x
(lo vedremo meglio tra poco applicato alla velocità)
x
Tangente alla
curva nel punto
(x,y(x))
y(x)
y( x  x)  y ( x)
dy
y
 lim
 lim
dx x0 x x0
x
Derivata di y(x) rispetto ad x
x+x
y
x
x
Derivate definite
da
0
dx
a  cost
d ax n 
 nax n1
dx
a  cost
La derivata di una costante è identicamente nulla
dx n
 nx n 1
dx
dx 4
 4x 3
dx
d sin x
 cos x
dx
d sin ax
 a cos ax
dx
d cos x
  sin x
dx
d cos ax
 a sin ax
dx
d tan x
1

dx
cos 2 x
d tan ax
a

dx
cos 2 ax
de ax
 ae ax
dx
d ln ax 1

dx
x
a  cost
a  cost
Proprietà delle derivate
Derivata di una somma(differenza) di funzioni:
d
 f x   g x   df  dg
dx
dx dx
d
(4 x 2  3 sin 2 x)  8 x  6 cos 2 x
dx
Prodotto di funzioni:
d
 f x g x   f dg  g df
dx
dx
dx
Rapporto di funzioni:
d
 f x  g x  
dx
g
df
dg
f
dx
dx
2
g
Funzione di funzione:
d
df dg
g  f x  
dx
dx df
d 3
[ x cos 3x]   x 3  3 sin 3x  cos 3x  3x 2 
dx
3x 2 cos 3x  3x 3 sin x
d  cos 3x   x 3  3 sin 3x  cos 3x  3x 2


3
6


dx  x 
x
x sin 3x  cos 3x
 3x 2

6
x
x sin 3x  cos 3x
3
x4
y ( x)  cos x,
g ( y)  y 2
d
(cos x) 2  2cos
x
sin
x  2 sin x cos x





dx
d
dy( x )
dx
gy
dx
Calcolo integrale
L’integrazione è da considerare la funzione inversa della derivata
L’integrale I della funzione f(x) tra i limiti a e b si scrive:
x b

x a
f ( x)dx  I ( x) a  I (b)  I (a)
b
f(x)
f(x)
ed è pari all’area compresa tra la curva f(x) e l’asse delle x
nell’intervallo di valori a≤ x≤b
NB:
Se il limite superiore dell’integrale è una variabile w si ha :
xw
I ( w) 

f ( x)dx
xa
allora
a
b
x
xw
d
d
I ( w) 
f ( x)dx  f ( w)

dw
dw x a
e quindi in generale:
L’integrale indefinito I(x) di f(x) è la funzione la cui derivata è f(x)
Es:
a
b
 ax

1
0
2

 bx  c dx  x 3  x 2  cx  d
3
2

1
b
b
b
a

a
 a
 a b
ax 2  bx  c dx   x 3  x 2  cx  d    13  12  c1  d    03  02  c0  d     c
2
2
2
3
0 3
 3
 3 2
Calcolo Integrale(2)
L’integrale I ( x)   f ( x)dx è detto primitiva di f(x), cioè è quella funzione che
quando derivata dà la funzione f(x)
NB: l’integrale è definito sempre a meno di una costante, cioè esistono infinite
primitive di una stessa funzione, tutte quelle che differiscono tra di loro per una
costante, in quanto la derivata di una costante è comunque nulla.
Proprietà degli integrali:
 dx  x  c
df x 
 dx dx  f ( x)  c
 af xdx  a f ( x)dx
dove a  cost
 af ( x)  bg ( x)dx  a f ( x)dx  b g ( x)dx
f
'
( x) g ( x)dx  f ( x) g ( x)   g ( x) f ( x)dx
'
L’integrale di una funzione moltiplicata per una
costante è uguale alla costante per l’integrale della
funzione
L’integrale di una somma di funzioni è uguale alla
somma degli integrali delle singole funzioni
Integrazione per parti: date due funzioni di x f e g
l’integrale della derivata di f moltiplicata per g è uguale
al prodotto delle due funzioni meno l’integrale della
derivata di g moltiplicata per f.