Esperimentazioni di Fisica 3 LA LINEA DI TRASMISSIONE

Esperimentazioni di Fisica 3
LA LINEA DI TRASMISSIONE
M. De Vincenzi
Dipartimento di Fisica, Università di Roma Tre
5 ottobre 2011
1
Introduzione alla trasmissione dei segnali
La schematizzazione e i metodi risolutivi dei circuiti formati da singoli componenti sono
valide fino a quando le dimensioni lineari dei componenti possano essere considerate piccole
rispetto alla lunghezza d’onda del campo elettromagnetico presente all’interno del componente stesso. In altre parole il campo elettromagnetico all’interno di ogni componente
circuitale si deve poter considerare costante all’interno della sua dimensione geometrica.
Quando è verificata questa condizione si parla di circuiti a costanti concentrate.
Al crescere della frequenza del segnale la sua lunghezza d’onda diminuisce e se diviene
confrontabile con le dimensioni dei componenti, la condizione che definisce i circuiti a costanti
concentrate, non è più verificata; in questo caso si parla di circuiti a costanti distribuite che
richiedono di sviluppare un apposito metodo di analisi.
Consideriamo ad esempio, un segnale sinusoidale di frequenza ν = 300M Hz, supponendo
che si propaghi alla velocità della luce c, la sua lunghezza d’onda è λ = c/ν ∼ 1m e la
distanza che separa la sua ampiezza massima da quella minima è λ/4 = 25 cm. Se il circuito
nel quale si propaga questo segnale ha una dimensione confrontabile con λ ci troviamo nella
situazione di un circuito a costanti distribuite. In elettronica è spesso necessario collegare tra
loro circuiti fisicamente separati (fino a distanze di chilometri) per permettere lo scambio
di informazioni (segnali). Un esempio molto comune di tali collegamenti è fornito dagli
impianti domestici di ricezione televisiva. L’impianto televisivo consisite in un antenna,
dispositivo che, potremo pensare, generi il segnale1 e da un circuito che riceve, amplifica
e decodifica questo segnale: il televisore. La distanza tipica tra antenna e televisore è
1 Più correttamente l’antenna seleziona segnali particolari tra quelli presenti nell’etere e li trasferisce ai
suoi terminali d’uscita. Nella maggior parte delle trasmissioni, il segnale televisivo è in un intervallo di
frequenze detto “Ultra High Frequency ” (UHF), sigla internazionale per indicare l’intervallo di frequenze
0.3 ÷ 3 GHz, (λ = 1 ÷ 0.1m)
1
i(x,t)
i(x+dx,t)
Rdx
v(x,t)
Ldx
Cdx
gdx
v(x+dx,t)
dx
Figura 1: Schematizzazione di un elemento di linea di trasmissione.
qualche decina di metri e questi due circuiti vengono connessi tra loro tramite un terzo
circuito, comunemente noto come cavo di antenna TV, che ha lo scopo di trasmettere il
segnale captato dall’antenna al televisore senza deformare il segnale. Confrontando l’ordine
di grandezza della lunghezza del cavo d’antenna TV (' 10 m) con quello della lunghezza
d’onda dei segnali televisivi (' 1 m), deduciamo che all’interno del cavo il campo e.m. non è
costante e dovremo schematizzare il comportamento del cavo con un’apposita metodologia
di analisi, adatta ai circuiti a costanti distribuite, che verrà esposta nei prossimi paragrafi.
2
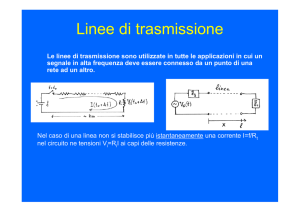
Linee di Trasmissione
I circuiti con i quali si trasportano i segnali elettrici prendono il nome di linee di trasmissione.
Le linee di trasmissione sono l’insieme di due conduttori per i quali una delle dimensioni
spaziali sia molto maggiore delle altre due e la cui sezione normale alla dimensione maggiore,
sia costante in forma e dimensioni. Affinchè si possa parlare di linea di trasmissione i due
conduttori devono essere in condizioni di induzione elettrostatica completa e non vi deve
essere flusso del campo di induzione magnetica disperso. Esempi di linee di trasmissione sono
1) due fili che corrono paralleli tra di loro a distanza costante, 2) due conduttori cilindrici
coassiali di raggio differente, 3) un filo o una sbarretta che corre parallelo ad un piano di
massa, eccetera (vedi ad esempio la figura 2).
2.1
Schematizzazione della linea di trasmissione
Per analizzare quantitativamente il comportamento di una linea di trasmissione è stato elaborato un modello nel quale un elemento infinitesimo dx di una linea è schematizzato da un
insieme di componenti a costanti concentrate come mostrato in figura 1). In questa schematizzazione, la linea di trasmissione è un circuito passivo formato da componenti (resistenze,
induttanze e capacità) distribuite lungo l’intera lunghezza della linea ed è caratterizzato dai
seguenti quattro parametri fondamentali:
1. la resistenza per unità di lunghezza R , che rappresenta la resistenza ohmica del filo
con cui è fatta la linea.
2
2. l’induttanza per unità di lunghezza L, che dipende (tranne casi particolari) soltanto
dalla geometria della linea.
3. la capacità (detta di shunt) per unità di lunghezza C, che dipende dalla geometria
della linea e dalla costante dielettrica dell’isolatore che separa i due conduttori che
formano la linea.
4. La conduttanza per unità di lunghezza g, che tiene conto delle perdite del dielettrico.
Applicando le leggi di Kirchhoff all’elemento di linea rappresentato nella figura 1 otteniamo le seguenti equazioni:
∂i
∂v
dx
= Rdx i + Ldx
v− v+
∂x
∂t
∂v
∂
∂v
∂i
dx + v +
dx gdx + Cdx
v+
dx
i =
i+
∂x
∂x
∂t
∂x
semplificando e trascurando i differenziali di secondo ordine si ottiene
−
∂v
∂i
= Ri + L
∂x
∂t
(1)
−
∂i
∂v
= gv + C
∂x
∂t
(2)
Risolvendo questo sistema di equazioni differenziali alle derivate parziali e aggiungendo le
condizioni al contorno, siamo in grado di calcolare la tensione e la corrente in funzione della
coordinata x lungo la linea e del tempo t. Scriviamo ora un’equazione nella quale appaia
solo la tensione v(x, t). Allo scopo deriviamo le equazioni precedenti, la prima rispetto a x e
la seconda rispetto a t; cosı̀ facendo si può eliminiare il termine di derivata mista ∂ 2 i/∂t∂x:
LC
∂2v
∂2v
∂v
−
+ (gL + RC)
+ gRv = 0
∂t2
∂x2
∂t
(3)
(si lascia come esercizio ricavare l’equazione analoga alla (3) nella quale compaia unicamente
la corrente i(x, t)). Questa equazione è nota come equazione dei telegrafisti, in quanto
descrive la trasmissione dei segnali attraverso i conduttori che venivano usati nei telegrafi a
filo. Se ci si limita al caso di linee prive di perdite, ovvero con resistenza del cavo trascurabile
(R = 0) e senza perdite nel dielettrico (g = 0), la (3) si semplifica nella:
LC
∂2v
∂2v
−
=0
2
∂t
∂x2
(4)
che è la nota equazione che descrive propagazione delle onde in una dimensione. La velocità
u, di propagazione dell’onda è data da:
u= √
3
1
LC
Si ricorda che la soluzione della (4) è:
Ff (x − ut) + Fb (x + ut)
(5)
dove con Ff eFb si indicano due funzioni qualsiasi (purché derivabili fino al secondo ordine).
E’ facile convincenrsi che Ff e Fb rappresentano dei segnali che si propagano rispettivamente
nella direzione positiva e in quella negativa delle x Quindi possiamo concludere che la linea di
trasmissione ideale (R = g = 0) permette la propagazione di segnali di tensione (di corrente)
√
senza introdurre deformazione della forma del segnale, con una velocità u = 1/ LC.
3
Soluzione dell’equazione dei telegrafisti
Torniamo ora alla soluzione generale del sistema di equazioni che porta all’equazione dei
telegrafisti. Per la soluzione utilizziamo il metodo della trasformata di Fourier che, in pratica,
equivale ad inviare in ingresso alla linea un segnale sinusoidale di pulsazione ω. Ponendo
v(x, t) = V (x) exp(jωt), le equazioni (1) e (2) divengono

dV


− dx = (R + jωL)I = Zo I


− dI = (g + jωC)V = Y V
o
dx
(6)
dove V = V (x) e I = I(x) sono la tensione la corrente complesse, e sono state introdotte le
quantità Zo e Y0 dette rispettivamente impedenza complessa, e ammettenza complessa per
unità di lunghezza della linea. Si noti che Zo 6= Yo−1 . Derivando rispetto ad x le (6) si arriva,
con facili passaggi alle relazioni seguenti:
d2 V
dx2
d2 I
dx2
= Zo Yo V
(7)
= Zo Yo I
(8)
Le equazioni (7) e (8) sono un’altra forma con cui si può scrivere l’equazione dei telegrafisti
quando si cerchino soluzioni di tipo armonico. Nelle (7) e (8) tensione e corrente compaiono
in modo completamete simmetrico, quindi sarà sufficiente ottenere la soluzione per la tensione o per la corrente. Per la tensione la soluzione generale dell’equazione differenziale (7)
è
V (x) = Vf e−γx + Vb eγx
(9)
dove la costante γ, detta costante di propagazione della linea, vale:
γ=
p
p
Zo Yo = (R + jωL)(g + jωC),
4
(10)
e Vf e Vb sono costanti di integrazione complesse che hanno dimensioni di una tensione.
Possiamo ora ricavare l’espressione per la corrente dalla (6)
I=−
1 dV
=
Zo dx
r
Yo
(Vf e−γx − Vb eγx )
Zo
Definendo l’impedenza caratteristica della linea come
r
Zc =
la corrente I si scrive come:
I=
Zo
=
Yo
s
R + jωL
g + jωC
(11)
Vf −γx Vb γx
e
−
e
Zc
Zc
(12)
Separando γ in parte reale e parte immaginaria, γ = α + jβ, si ottiene l’andamento nello
spazio e nel tempo della tensione e della corrente
v(x, t) = Vf e−αx ej(ωt−βx) + Vb eαx ej(ωt+βx)
i(x, t) =
Vb αx j(ωt+βx+φ)
Vf −αx j(ωt−βx+φ)
e
e
−
e e
|Zc |
|Zc |
(13)
(14)
Nella (13) riconosciamo un onda progressiva (ej(ωt−βx) ), ovvero diretta nella direzione positiva delle x, di ampiezza Vf modulata da un esponenziale decrescente (e−αx ), ed un onda
regressiva (ej(ωt+βx) ), ovvero diretta nella direzione negativa delle x, di ampiezza Vb , modulata da un esponenziale crescente(eαx ). I suffissi f e b stanno ad indicare i termini inglesi
forward e backward che ricordano la direzione dell’onda. La corrente che passa nella linea
in funzione del tempo e della posizione è data dalla (14); si noti che il segnale di corrente
risulta proporzionale alla tensione soltanto per il singolo modo di propagazione.
3.1
Linea priva di perdite
Nella definizione dell’impedenza caratteristica Zc , se R = g = 0, ovvero se la linea non ha
perdite ohmiche, oppure se stiamo considerando una frequenza ω sufficientemente elevata
per cui R ωL e g ωC allora:
r
Zc =
Zo
=
Yo
s
R + jωL
→
g + jωC
r
L
C
(15)
In questa condizione l’impedenza caratteristica subisce due importanti semplificazioni che
caratterizzano il funzionamento usuale di una linea di trasmissione:
1. Zc diviene reale e quindi lo sfasamento tra corrente e tensione risulta nullo, come
accade con le resistenze.
5
2. Zc risulta indipendente da ω e ciò permette la propagazione di segnali non sinusoidali
nella linea senza deformazione.
La condizione che si esplora (R e g nulli o trascurabilmente piccoli) porta ad una importante
semplificazione anche per γ, che per R → 0 e g → 0 si riduce a:
γ=
p
√
(R + jωL)(g + jωC) → jω LC
(16)
γ è completamente immaginario e coincide con jβ; essendo β legato alla velocità di propagazione dell’onda, (β = ω/u), otteniamo nuovamente la, già nota, velocità di propagazione
del segnale:
u= √
1
LC
(17)
La relazione (17) sembra legare la velocità di propagazione delle onde nella linea anche alle
caratteristiche geometriche della stessa linea. Tuttavia, si può dimostrare che se L e C sono
indipendenti da x, la velocità di propagazione dell’onda dipende soltanto dalle caratteristiche
elettromagnetiche del mezzo in cui l’onda si propaga, ovvero:
u= √
1
1
c
=√ '√
µ
LC
(18)
dove c è la velocità della luce nel vuoto e, per l’ultima eguaglianza, si è fatto uso dell’osservazione che generalmente nella costruzione di linee di trasmissione non si usano materiali
ferromagnetici, per cui si ha µr ' 1.
3.2
Parametri delle linee di trasmissione
Linee di trasmissione comuni sono: i) quelle realizzate tramite due fili di diametro d paralleli
e posti ad una distanza D, ii) quelle realizzate tramite due conduttori cilindrici coassiali di
raggi a (interno) e b (esterno) (cavo coassiale) iii) quelle realizzate da una striscia conduttrice
di larghezza w, posta a distanza δ dal piano di massa e iv) quelle realizzate da un filo di
diametro d che corre a distanza δ parallelamente al piano di massa (vedi figura 2).
a)
11111
00000
00000
11111
111111
000000
000000
111111
b)
c)
11111
00000
00000
11111
00000
11111
00000
11111
00000
11111
00000
11111
d)
Figura 2: Sezioni delle linee di trasmissione più comuni. a) linea bifilare; b) sriscia (strip) su
piano di massa; c) filo su piano di massa; d) cavo cavo coassiale.
La forma più diffusa delle linee di trasmissione è il cavo coassiale che ha una capacità
6
Tabella 1: Parametri di alcune linee di trasmissione
Parametri
L
C
Coppia di fili
µ
ln D/d
π
π/ ln D/d
per unità di lunghezza pari a:
C = r o
Cavo cossiale
µ
ln b/a
2π
2π/ ln b/a
2π
ln D/d
Striscia
µδ/w
w/δ
(19)
dove D e d sono rispettivamente il diametro del conduttore cavo esterno ed il diametro del
filo più interno. Dalla relazione (18) ricaviamo facilmente l’induttanza per unità di lunghezza
della linea come:
L = µ
ln D/d
1
=µ
C
2π
Nella tabella 3.2 sono riportati i valori dei parametri che caratterizzano le linee (ideali) sopra
descritte.
Nota la capacità per unità di lunghezza di una configuazione di conduttori formanti
una linea, l’induttanza per unità di lunghezza è ottenibile anche dalla relazione che lega la
velocità alle caratteristiche del mezzo della linea.
I valori della impedenza caratteristica ottenibili con linee reali sono compresi nell’intervallo 10–200Ω
3.3
Riflessioni nelle linee di trasmissione
In questo paragrafo volgliamo studiare come si comporta una linea di trasmissione di lunghezza finita l quando viene chiusa su un carico che per semplicità considereremo resistivo
(vedi figura 3 ).
La soluzione generale per la trasmissione di un segnale attraverso una linea di trasmissione ideale è formata dalla somma di due onde: una progressive, ovvero che si propaga nella
direzione positiva delle x, l’altra regressiva, ovvero che si propaga nella direzione negativa
delle x:
v=
vf + vb
(20)
i=
(vf − vb )/Rc
(21)
Supponiamo ora di connettere un generatore di gradino di tensione V ed impedenza interna
Rg ad una linea di lunghezza l chiusa su una resistenza R (vedi la figura 3) All’istante t = 0
la linea (ideale) si comporta come una resistenza di valore Rc . Per cui ai suoi terminali
d’ingresso appare una tensione
vf =
Rc
V
Rc + Rg
7
(22)
Rg
V
R
Rc
l
Figura 3: Linea di trasmissione chiusa su un carico R
La corrente che scorre dentro la linea è data dal rapporto tra la tensione dell’onda progressiva
con il valore della resistenza caratteristica if = Vf /Rc . Il fronte d’onda si propaga nella
√
√
linea con velocità u = 1/ LC e dopo un tempo l LC raggiunge la terminazione della
linea. Qui è presente una discontinuità rappresentata dalla resistenza di carico della linea
R. Affichè siano rispettate sia la legge di Ohm sulla resistenza di terminazione della linea, sia
l’equazione differenziale di propagazione, si deve trovare una combinazione di onde dirette
(vf ) e riflesse (vb ), tali che sia valida la legge di Ohm sulla resistenza di terminazione:
R=
vf + v b
(vf − vb )/Rc
(23)
Esprimiamo l’ampiezza (vb ) dell’onda riflessa come una frazione di quella dell’onda incidente
ponendo vb = ρvf , dove è stato introdotto il parametro ρ detto coefficiente di riflessione.
Con facili passaggi si ottiene la seguente espressione del coefficiente di riflessione:
ρ=
R − Rc
R + Rc
(24)
Sono notevoli i casi :
• R = ∞: Linea aperta in questo caso ρ = 1, l’onda progressiva viene riflessa con lo
stesso segno ed ampiezza.
• R = 0: Linea in corto in questo caso ρ = −1, l’onda progressiva viene riflessa con la
stessa ampiezza ma con segno opposto.
• R = Rc : Linea adattata in questo caso ρ = 0, non si ha quindi nessuna riflessione e la
linea terminata sulla sua impedenza caratteristica è equivalente ad una linea infinita.
3.4
Linea in corto circuito e linea aperta
Si consideri un circuito come quello di figura 3 con R = 0. Si supponga che V sia un gradino
V (t) = V0 θ(t). Come si presenta il segnale all’ingresso della linea? Quello che succede
è schematizzabile come segue: al tempo t = 0 il segnale inizia a propagarsi nella linea
(supposta priva di perdite), al tempo t = l/u il segnale arriva alla terminazione dove R = 0
8
Linea aperta
Linea in corto
V
V
t
t
Figura 4: Segnali in ingresso ad una linea aperta e ad una linea in corto sollecitata da un
gradino di tensione
ρ
ρ
f
b
4t d
v
v5 = ρ b 4
v4 = ρ
2t d
v
v3 = ρ b 2
v2 = ρ
f v3
5td
3td
f v1
td
v1
t=0
x=0
x=l
Figura 5: Diagramma utile al calcolo dell’ampiezza dei segnali che percorrono una linea non
adattata ad entrambe le estremità.
e quindi ρ = −1; ne consegue che si genera un’onda riflessa (regressiva ovvero che si propaga
nella direzione negativa delle coordinate) di ampiezza uguale ed opposta a quella incidente,
e dopo un tempo pari a t = 2l/u questa onda torna all’ingresso della linea. L’ampiezza del
gradino incidente vale:
Vf = V0
Rc
Rc + Rg
per t < 2l/u, per t > 2l/u all’onda diretta si somma algebricamente l’onda riflessa di
ampiezza Vb = −Vf che azzera l’onda incidente.
Nel caso in cui la linea sia aperta (R = ∞) si ottiene ρ = +1 e si può ripetere lo stesso
ragionamento seguito per la linea in corto circuito, con la differenza che alla fine Vb = +Vf
e l’onda riflessa si aggiunge a quella diretta. Si noti che fino all’istante t = 2l/u il segnale
all’ingresso della linea è uguale nei due casi: linea in corto e linea aperta. Gli andamenti
temporali della tensione all’ingresso della linea sono mostrati per i due casi considerati nella
figura 4
9
v
v
x=l
x=0
2
4
6
8
10
12
2
t/td
4
6
8
10
12
Figura 6: Andamento dei segnali in ingresso ed in uscita per una linea disadattata ad entrambe le estremità e sollecitata da un impulso a gradino. In ingresso la linea è chiusa su
Rc /3 e il coefficiente di riflessione è ρb = −1/2, in uscita la linea è aperta e il coefficiente
di riflessione è ρf = 1.
3.5
Riflessioni Multiple
Nel caso che la linea non sia adattata ad entrambe le estremità, si verifica il fenomeno delle
riflessioni multiple. Esaminiamo quanto già descritto nel paragrafo precedente supponendo
che la resistenza del generatore sia differente da quella caratteristica della linea Rg 6= Rc
e che la linea sia chiusa su un carico R. Quindi le onde progressive che raggiungono il
carico R saranno riflesse con un coefficiente di riflessione ρf = (R + Rc )/(R − Rc ), mentre le
onde regressive saranno riflesse con un coefficiente di riflessione ρb = (Rg + Rc )/(Rg − Rc ).
Supponiamo che il generatore generi un gradino di tensione v(t) = V0 θ(t); non è difficile
verificare che l’ampiezza del segnale che si propaga nella linea è V1 = V0 Rc /(Rg + Rc ). Di
questo segnale, una volta raggiunta la terminazione della linea, ne verrà riflessa una frazione
ρf ; il segnale regressivo di ampiezza V2 = ρf V1 , una volta ritornato all’ingresso della linea,
verrà a sua volta riflesso dando luogo a un’onda progressiva di ampiezza ρb V2 , che si andra a
sommare al segnale già presente. Nella figura 5 è rappresentato un diagramma utile alla per
il calcolo dell’ampiezza di segnali che si riflettono alle estremità di una linea non adattata
ad entrambe le estremità.
Il fenomeno, nel caso di linee ideali non dissipative, continua nel modo descritto all’infinito. Un esempio del fenomeno delle riflessioni multiple è mostrato nella figura 6.
4
Attenuazione del segnale nella linea
Nel caso in cui i termini dissipativi (R e g ) non possano essere trascurati, la parte reale del
coefficiente di propagazione γ (si veda la 10) sarà responsabile dell’attenuazione del segnale
mentre quest’ultimo si propaga lungo la linea. Possiamo ottenere per γ delle espressioni
semplificate nel limite di frequenza che tende all’infinito2 e nel limite di frequenza che tende
2 Il comportamento asintotico che si cerca inizierà quando saranno verificate entrambe le seguenti
condizioni: ω R/L e ω g/C.
10
t/td
a zero3 .
√
Per ω → ∞, mettendo in evidenza jω LC ovvero l’espressione che si ottiene per una
linea priva di perdite, si ha:
γ=
p
√
(R + jωL)(g + jωC) = jω LC
s
R
1+
jωL
1+
g
jωC
utilizzando l’espansione di Taylor della radice ed arrestandosi al primo ordine si ha:
√
√
1 R
1 R
g
γ ' jω LC 1 − j
+
= jω LC +
+ gRc =
2 ωL ωC
2 Rc
Per ω → 0,
γ=
p
(R + jωL)(g + jωC) −→
p
Rg
(25)
L’ultimo termine nella (25), quello reale, rappresenta l’effetto dell’attenuazione del segnale
lungo la linea dovuto alla presenza di effetti dissipativi nella linea. Si noti che il coefficiente
di attenuazione dato dalla (25) è indipendente dalla frequenza.
Attenuazione in una linea in corto circuito. In questo paragrafo mostriamo come
si possa stimare il parametro di attenuazione α di una linea di trasmissione. Allo scopo
alimentiamo la linea con un segnale a gradino di ampiezza Vo generato da un alimentatore
cui impedenza interna sia uguale all’impedenza caratteristica della linea Rg = Rc . La
linea considerata sia di lunghezza l e in corto circuito all’estremità opposta a quella del
generatore ( vedi la figura 3 ponendo Rg = Rc e R = 0). Al tempo t = 0, come abbiamo
già visto, l’ampiezza del segnale in ingresso alla linea è Vo /2. Dopo un tempo pari a 2l/u il
segnale torna all’ingresso della linea invertito (in quanto ρ = −1) e di ampiezza attenuata
di un fattore e−2lα . Indicando con nVin la tensione misurata all’ingresso della linea avremo
quindi:
Vin =
Vo
(1 − e−2αl ) ' Vo αl
2
dove l’ultima relazione è stata ottenuta sviluppando in serie l’esponenziale. Se indichiamo
con il valore della tensione misurata in ingresso alla linea per tempi maggiori di 2l/u, siamo
in grado di valutare il parametro α. Infatti, con semplici calcoli, si ottiene:
α=
Vo l
3 Il comportamento asintotico che si cerca inizierà quando saranno verificate entrambe le seguenti
condizioni: ω R/L e ω g/C.
11
5
Linea in regime sinusoidale
Consideriamo una linea di lunghezza l connessa a un generatore sinusoidale di pulsazione
ω che supponiamo avere un’impedenza d’uscita pari all’impedenza caratteristica della linea.
Se l’estremità della linea, opposta a quella del generatore, è chiusa su un carico di impedenza
ZL , il coefficiente di riflessione vale ρ = (ZL − Rc )/(ZL + Rc ). Calcoliamo l’impedenza in
ingresso della linea in questa condizione. Si ricordi che l’impedenza d’ingresso è data dal
rapporto tra la tensione presente all’ingresso e la corrente d’ingresso.
Avendo supposto che l’impedenza di uscita del generatore sia pari all’impedenza caratteristica della linea, ne segue che il coefficiente di riflessione per segnali che arrivano all’ingresso
della linea è nullo. Possiamo quindi affermare che l’ampiezza del segnale in ingresso è data
dalla somma dell’onda diretta più quella riflessa:
vin (x, t) = vf ejωt + vb ejωt−γ2l
ponendo vb = ρvf .
vin (x, t) = vf (ejωt + ρ ejωt−γ2l )
(26)
Dalla (??) possiamo ottenere la corrente d’ingresso la cui espressione è:
iin (x, t) = [vf (ejωt − ρ ejωt−γ2l )]/Rc
(27)
Per cui l’impedenza d’ingresso vale:
Zin = Rc
1 + ρ eγ2l
1 − ρ eγ2l
(28)
Se la linea può essere considerata ideale, allora per la (16), γ è puramente immaginario
√
e coincide con jβ = jω LC. In questa ipotesi, usando la la relazione di Eulero, si può
scrivere:
Zin = Rc
ZL + jRc tan βl
Rc + jZL tan βl
L’espressione precedente si semplifica ulteriormente supponendo che la linea sia in corto
circuito, ovvero ZL = 0; in questa condizione la sua impedenza di ingresso vale
Zin = jRc tan βl
(29)
L’andamento del rapporto tra il modulo dell’impedenza Zin e l’impedenza caratteristica
√
della linea in funzione della pulsazione moltiplicata per LC è mostrato nella figura 7. Si
noti che, in condizioni ideali, questa impedenza varia tra 0 e ∞. Tale proprietà può essere
verificata in un esperienza di laboratorio misurando l’andamento della tensione di ingresso
in funzione della frequenza in una linea adattata in ingresso e in corto circuito nell’altra
12
Figura 7: Andamento con la frequenza angolare dell’impedenza di ingresso di una linea in
corto circuito.
estremità.
13
Problemi
1.Si calcoli il ritardo di un segnale di 100 M Hz trasmesso mediante una linea di trasmissione
uniforme di lunghezza 10 m. Le proprietà sono tali che la lunghezza d’onda del segnale nella linea
risulta essere 1 m. [R.10−8 s]
2. Per ottenere impulsi brevi, dell’ordine della decina di nanosecondi, ed alta tensione (dell’ordine
delle centinaia di kV ) si può usare il dispositivo, detto Blumlein schematizzato nella figura 8. Il
HV
Zo
Zo
2Zo
2Zo
SG
Figura 8: Schema della Blumlein per la generazione di impulsi brevi ed ad alta tensione
dispositivo consiste di due conduttori affacciati in modo da formare una linea di impedenza caratteristica 2Zo . Per una frazione della linea è inserito, tra i due, un terzo conduttore in modo da formare
una linea di impedenza Zo . L’elettrodo centrale viene caricato alla tensione V , quindi, tramite un
dispositivo detto spark–gap comandata viene chiuso l’interruttore SG. Spiegare il funzionamento
del circuito.
3. Fino agli anni 70 era di uso comune nei laboratori l’impulsatore a relais di vapori di mercurio.
Lo schema di questo impulsatore, che permetteva di raggiungere tempi di salita migliori del nanosecondo, è mostrato in figura 9. Spiegare il funzionamento del circuito tenendo conto che il relais a
contatti bagnati nel mercurio è un interruttore che può essere considerato ideale.
Relais
Rg
V
Rc
utilizzo
l
Figura 9: Schema dell’impulsatore a relais a contatti bagnati nel mercurio
4. Un modo per ottenere impulsi di breve durata, a partire de un generatore di tensione a gradino,
è mostrato nella figura 10. Spiegare il funzionamento del circuito
R
utlizzo
Rg
V
l
Figura 10: Generatore di impulsi brevi
5. In una casa arriva un unico cavo di antenna TV (Zc = 75Ω) che deve servire due televisori
lontani tra loro. Gli apparecchi televisivi hanno un’impedenza d’ingresso di 75Ω e vanno collegati
con un cavo a 75 Ω. Come si deve effettuare il collegamento per evitare che nella connessione non
vi siano riflessioni, avendo a disposizione solo dei resistori?
14