Linee di trasmissione

Linee di trasmissione
Le linee di trasmissione sono utilizzate in tutte le applicazioni in cui un
segnale in alta frequenza deve essere connesso da un punto di una
rete ad un altro.
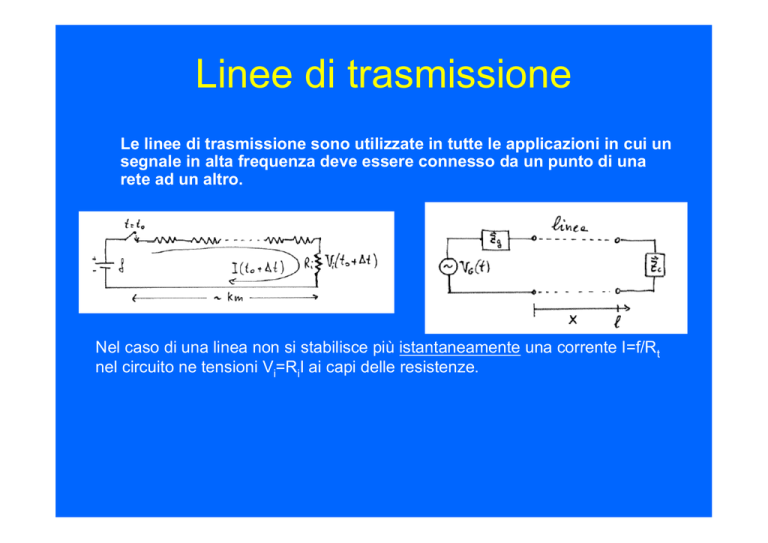
Nel caso di una linea non si stabilisce più istantaneamente una corrente I=f/Rt
nel circuito ne tensioni Vi=RiI ai capi delle resistenze.
Linee di trasmissione
La linea rappresenta un sistema
a parametri distribuiti
•
•
•
•
•
•
•
•
•
•
RA è la resistenza del conduttore A nel tratto dx, dovuta alla resistività del cavo.
Considerando una resistenza unitaria RAu per unità di lunghezza, RA è data
da RAu dx.
RB rappresenta l’analoga grandezza per il conduttore B.
LA è l’induttanza del tratto dx che, nuovamente, può essere espressa come LAu dx,
ove LAu è l’induttanza per unità di lunghezza.
LB rappresenta l’analoga grandezza per il conduttore B.
G è la conduttanza fra i due conduttori nel tratto di cavo considerato, dovuta al
fatto che l’isolamento fra essi non è perfetto. In termini della conduttanza per
unità di lunghezza Gu, essa è data da G = Gu dx.
C è la capacità fra i due tratti di conduttore ed è anch’essa espressa in termini della
capacità per unità di lunghezza come C = Cu dx.
• Fra le posizioni x e x + dx lungo la linea tensione e corrente variano in quanto ci
sono cadute di tensioni, dovute a R e L, e perdite di corrente, dovute a G e C.
Linee di trasmissione
Induttanza per unità di lunghezza in
una linea coassiale
Capacità per unità di lunghezza in
una linea coassiale
Linee di trasmissione
Equazione dell’onda per il campo E
2

E
 2 E   2   2 E
t
E V
HI
'C
' L
 "  G
 "  R
Equazione dei telegrafisti
 2V
V
 2V
 RGV  ( LG  RC )
 LC 2
2
t
t
t

1
v 

LC
Linee di trasmissione
Onde elettromagnetiche
  j  
Linea di trasmissione
    j     j  
    j 
 R  j L  G  jC 
Fattore di propagazione

   j 

Z

   j 
Zc 
Impedenza
R  j L
G  jC
Linee di trasmissione
L’impedenza caratteristica di una linea di trasmissione è data dal
rapporto tra la tensione e la corrente per un segnale che si propaga
nella direzione positiva di x
L
Z0 
C
Per una linea coassiale è possibile calcolare la sua impedenza
caratteristica partendo dalle sue proprietà geometriche.
Linee di trasmissione
E’ interessante studiare il caso pratico in cui la linea sia di
lunghezza finita e presenti delle discontinuità relative, ad
esempio, alla presenza di carichi localizzati e/o a giunzioni
di tratti di linea con differente impedenza caratteristica.
Caso di una linea chiusa su un carico Z (si considereranno per
semplicità solo carichi resistivi).
Linee di trasmissione
Generatore di
tensione a gradino
di resistenza interna Rg
All’istante t=0 la linea si comporta come una resistenza di
valore Rc. Ai teminali d’ingresso appare una tensione
Rc
vf 
V
Rc  Rg
La corrente che scorre nella linea vale:
i  v f / Rc
Il gradino si propaga con velocità u=1/LC e raggiungerà la fine della
linea al tempo T = lLC.
Linee di trasmissione
Discontinuità rappresentata dalla
resistenza di carico alla fine della linea
vf
vb
Vf è un’onda progressiva
Vb è un’onda regressiva
R
Soluzione delle equazioni dei telegrafisti
che tenga conto della validità della legge
di Ohm per la resistenza di carico.
v f  vb
(v f  vb ) / Rc
vb   v f
R  Rc

R  Rc
Tensione riflessa
espressa in
funzione della
tensione incidente
Linee di trasmissione
Casi notevoli

R   La linea è aperta,  = 1 e l’onda progressiva viene riflessa con
stessa ampiezza e con lo stesso segno
Segnale d’ingresso
vf 
Rc
V
Rc  Rg
l lunghezza della linea
A t = l/u il gradino arriva alla fine della linea dove trova la
resistenza di carico e si avrà vb= vf + vf dove  vale +1.
A t = 2l/u il gradino riflesso arriva all’ingresso della linea
dove può essere visto e varrà ancora vb=vf + vf.
R  Rc
R  Rc
Linee di trasmissione
Casi notevoli
R  0 La linea è cortocircuitata,  = -1 e l’onda progressiva viene
riflessa con stessa ampiezza ma con segno opposto
Segnale d’ingresso
vf 
Rc
V
Rc  Rg
l lunghezza della linea
A t = l/u il gradino arriva alla fine della linea dove trova la
resistenza di carico e si avrà vb= vf + vf dove  vale -1
per cui vb = 0.
A t = 2l/u il gradino riflesso arriva all’ingresso della linea
dove può essere visto e varrà ancora vb= 0

R  Rc
R  Rc
Linee di trasmissione

Casi notevoli
R  Rc
R  Rc
R = Rc La linea è adattata  = 0 e l’onda progressiva non viene riflessa
V
Segnale d’ingresso
vf 
Rc
V
Rc  Rg
l lunghezza della linea
t
La linea è equivalente ad una linea di lunghezza infinita
Linee di trasmissione
Rg  Rc
Riflessioni multiple
Nel caso in cui una linea presenta un disadattamento in ingresso ed in
uscita si verificano all’interno della linea stessa delle riflessioni multiple
Segnale in ingresso
Rc
V
VG
Rc  Rg
Coefficienti di
riflessione
RL  Rc
R 
RL  Rc
RG  Rc
S 
RG  Rc
Linee di trasmissione
Rg  Rc
Riflessioni multiple
Nel caso in cui una linea presenta un disadattamento in ingresso ed in
uscita si verificano all’interno della linea stessa delle riflessioni multiple
RL  Rc
R 
RL  Rc
RG  Rc
S 
RG  Rc
Linee di trasmissione
Rg  Rc
Riflessioni multiple
Nel caso in cui una linea presenta un disadattamento in ingresso ed in
uscita si verificano all’interno della linea stessa delle riflessioni multiple
V  V   RV   S  RV   S  R2V   S2  R3V  ......
Linee di trasmissione
Rg  Rc
Riflessioni multiple
Nel caso in cui una linea presenta un disadattamento in ingresso ed in
uscita si verificano all’interno della linea stessa delle riflessioni multiple
Linee di trasmissione
Attenuazione del segnale lungo una linea
Trascurando la conduttanza di shunt si ottiene
Attenuazione
dovuta alle
caratteristiche
ohmiche del
materiale che
costituisce la linea
In generale:
V ( x)  V
 x
Dove:
Rdc

lRc