Matematica e Statistica (Beni culturali) a.a. 2016-2017
Soluzione esonero del 21-12-2016
L. Bertini - M. Isopi
Deve essere x 6= 0 perché il logaritmo sia definito e x 6= ±1 per evitare di dividere per 0. Poi:
lim
x→+∞
x
= +∞;
log |x|
x
= +∞;
x→−1 log |x|
lim
lim
x→−∞
x
= 0;
x→0 log |x|
lim
x
= −∞
log |x|
x
= −∞;
x→1 log |x|
lim
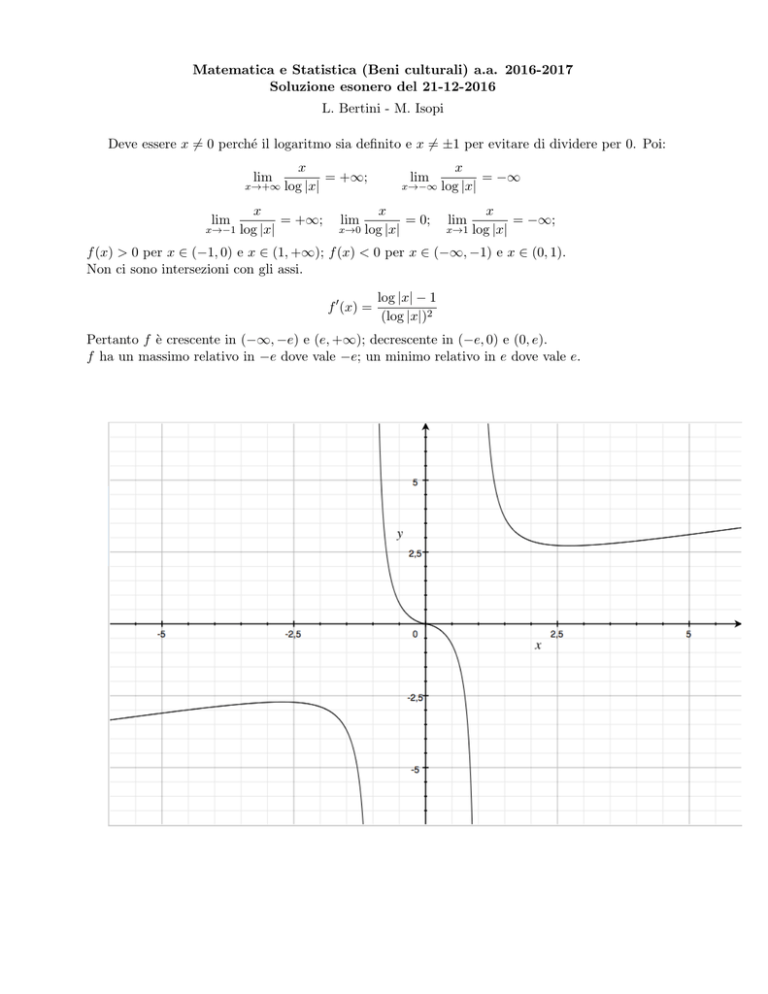
f (x) > 0 per x ∈ (−1, 0) e x ∈ (1, +∞); f (x) < 0 per x ∈ (−∞, −1) e x ∈ (0, 1).
Non ci sono intersezioni con gli assi.
f 0 (x) =
log |x| − 1
(log |x|)2
Pertanto f è crescente in (−∞, −e) e (e, +∞); decrescente in (−e, 0) e (0, e).
f ha un massimo relativo in −e dove vale −e; un minimo relativo in e dove vale e.












