- MATEMATICAeSCUOLA

Studio di due integrali doppi
Primo integrale
Calcolare il seguente integrale doppio
 x
E
essendo E il dominio E 
 x; y   R 1  x
2
2
2
y
dxdy
 y2

 y 2  4 x   y  3x .
Elaborazioni
1)
Il dominio E è la parte finita di piano contenuta nel primo e quarto quadrante avente come
frontiera un arco della circonferenza 1 : x 2  y 2  1 , che ha come centro l'origine degli assi
cartesiani e raggio unitario, un arco della circonferenza 2 : x 2  y 2  4 x  0 , che ha centro nel
punto C(2;0) e raggio 2, dal segmento della semiretta s1 : y  3x i cui estremi sono i punti in cui
questa incontra nel primo quadrante le due circonferenze 1, 2 e dal segmento della semiretta
s2 : y   3x i cui estremi sono i punti in cui questa incontra nel quarto quadrante le due
circonferenze 1, 2. I punti della frontiera indicata fanno tutti parte del dominio E, quindi questo è
chiuso e limitato.
2)
La funzione integranda nell'insieme E è continua e assume valori non negativi; poiché E è chiuso e
limitato il valore dell'integrale da calcolare è un numero positivo.
3)
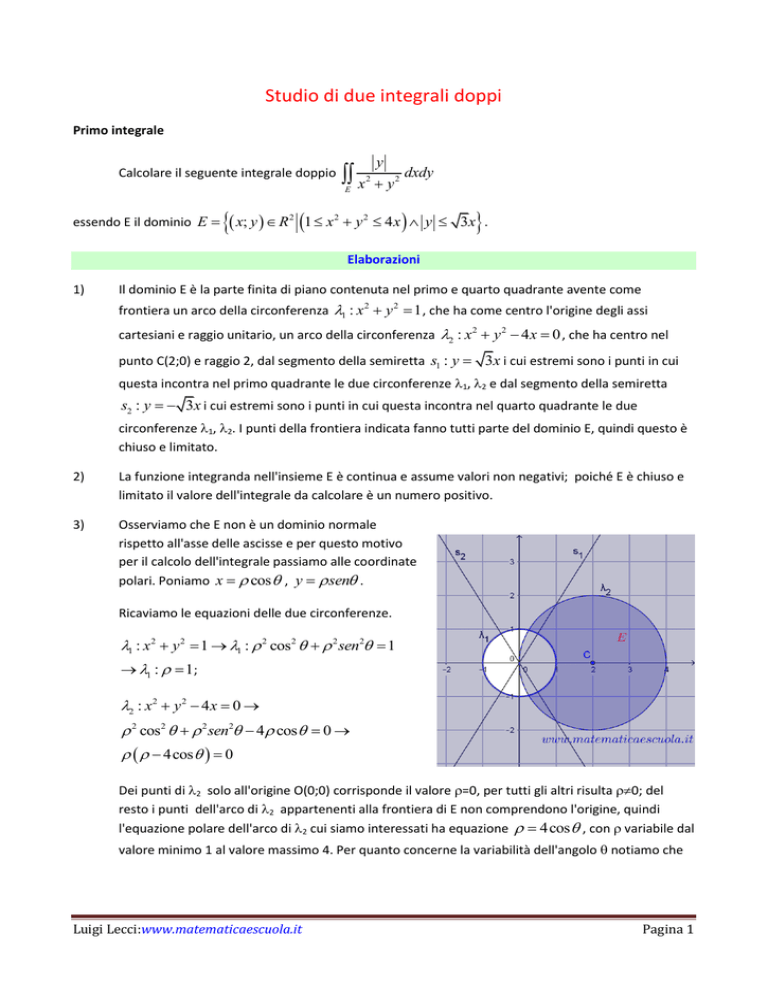
Osserviamo che E non è un dominio normale
rispetto all'asse delle ascisse e per questo motivo
per il calcolo dell'integrale passiamo alle coordinate
polari. Poniamo x   cos  , y   sen .
Ricaviamo le equazioni delle due circonferenze.
1 : x2  y 2  1  1 :  2 cos2    2 sen2  1
 1 :   1;
2 : x2  y 2  4 x  0 
 2 cos2    2 sen2  4 cos  0 
    4cos   0
Dei punti di 2 solo all'origine O(0;0) corrisponde il valore =0, per tutti gli altri risulta 0; del
resto i punti dell'arco di 2 appartenenti alla frontiera di E non comprendono l'origine, quindi
l'equazione polare dell'arco di 2 cui siamo interessati ha equazione   4cos  , con  variabile dal
valore minimo 1 al valore massimo 4. Per quanto concerne la variabilità dell'angolo  notiamo che
Luigi Lecci:www.matematicaescuola.it
Pagina 1
dai coefficienti angolari delle due semirette s1, s2 deduciamo che 

3
 

3
. Ebbene, un
qualsiasi punto P del dominio E ha coordinate polari (;), con 1    4cos  e
4)


3
 

3
.
Calcolo dell'integrale doppio
Facciamo presente che il calcolo effettivo dell'integrale doppio con le nuove coordinate (polari)
oltre che richiedere l'espressione della funzione integranda tramite le nuove variabili, è necessario
moltiplicare detta espressione per il modulo dello Jacobiano che ricordiamo è
x

J=
y

x
cos 


sen
y

  sen

 cos 
Inoltre, possiamo limitare la variabilità dell'angolo  all'intervallo 0   

3
perché sia il dominio E,
sia la funzione integranda sono simmetrici rispetto all'asse delle ascisse: per ogni punto P'(x;y) del
dominio E anche il punto P''(x;-y) appartiene al dominio e la funzione verifica la proprietà
f(x;y)=(f(x;-y).
Per questi motivi possiamo scrivere
f  x; y  
y
 sen
 sen
sen
;
 f  x   ;  ; y   ;    2


2
2
2
2
2
x y
 cos    sen 


2
considerare come dominio di integrazione in coordinate polari il sottoinsieme di R2

 

D    ;  1    4cos     0     
3 


scrivendo

y
sen
dxdy

2


d

d


2
E x2  y 2
D 
30


2 3 sen   1
 0
4cos


4cos
 1



sen d  d  2 3 sen
 0


4cos
 1

d  d 

d  2 3 sen  4cos   1 d  2 3 4sen cos  d  2 3 sen d 
 0

 0
 0
  

2 3 2sen  2  d  2  cos  03  2 cos  2  03  2 cos  03  2 cos  2    cos  0   
 0
  3




  

 1 
1 
2 cos    cos  0    2    1  2   1  3  1  2
 2 
2 
 3

*** ***
Luigi Lecci:www.matematicaescuola.it
Pagina 2
Secondo integrale (1)
Calcolare il seguente integrale doppio

E
y
x
2
y

2 2
dxdy , sempre con E 
 x; y   R 1  x
2
2

 y 2  4 x   y  3x
Osservazione
Per il calcolo dell'integrale proposto valgono tutte le considerazioni svolte nel calcolo dell'integrale
dell'esercizio precedente; la differenza consiste solo nella diversa forma analitica della funzione
integranda.
Riporto il calcolo senza ulteriori precisazioni.
Elaborazioni
2
D
sen
  d  d 
3

E


y
x
2
 y2 
2

 4cos sen

d   d 
dxdy  2 3  
2
 0
  1 


  1  4cos 
1


2 sen 
 d  d  2 sen    
 d  2 3 sen  
 1 d 
 1
 0
   1 
 4cos 






1 3  sen
1 1

1
3
3  2  cos  3 
ln    ln 1  
d


2
sen

d


ln
cos












0
0
 0
2 2
2  0 cos 
2


3
 0
4cos
2

3
 0
1 1

   1
2   cos    1    ln  2    2    2  ln  2   0, 6534
2 2
3  2

(1)
Esercizio assegnato nel compito di Analisi matematica II, C.d.L. in Ing. dell'Informazione, Lecce, il 13-02-2013
Luigi Lecci:www.matematicaescuola.it
Pagina 3