21 moto armonico

Prof. A. Di Muro
Moto armonico
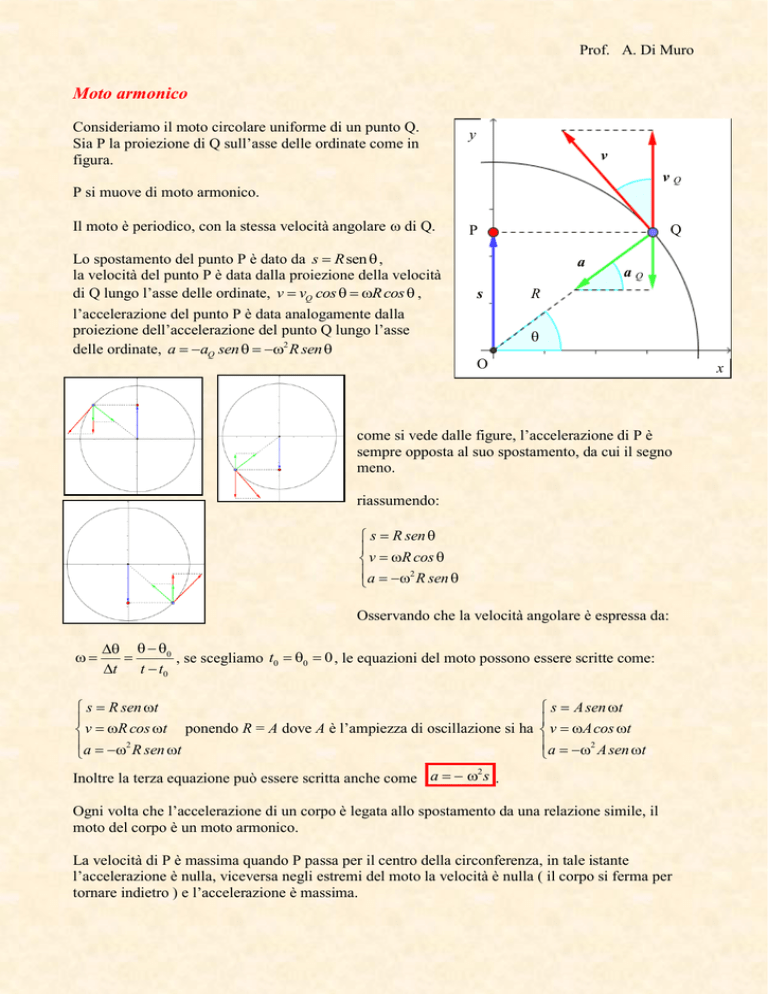
Consideriamo il moto circolare uniforme di un punto Q.
Sia P la proiezione di Q sull’asse delle ordinate come in
figura.
y
v
vQ
P si muove di moto armonico.
Il moto è periodico, con la stessa velocità angolare  di Q.
Lo spostamento del punto P è dato da s  R sen  ,
la velocità del punto P è data dalla proiezione della velocità
di Q lungo l’asse delle ordinate, v  vQ cos   R cos  ,
l’accelerazione del punto P è data analogamente dalla
proiezione dell’accelerazione del punto Q lungo l’asse
delle ordinate, a  aQ sen   2 R sen 
Q
P
a
s
aQ
R

O
x
come si vede dalle figure, l’accelerazione di P è
sempre opposta al suo spostamento, da cui il segno
meno.
riassumendo:
 s  R sen 

 v  R cos 
a  2 R sen 

Osservando che la velocità angolare è espressa da:

   0

, se scegliamo t0  0  0 , le equazioni del moto possono essere scritte come:
t
t  t0
 s  R sen t

 v  R cos t ponendo R = A dove A è l’ampiezza di oscillazione si ha
a  2 R sen t

 s  A sen t

 v  Acos t
a  2 A sen t

2
Inoltre la terza equazione può essere scritta anche come a    s .
Ogni volta che l’accelerazione di un corpo è legata allo spostamento da una relazione simile, il
moto del corpo è un moto armonico.
La velocità di P è massima quando P passa per il centro della circonferenza, in tale istante
l’accelerazione è nulla, viceversa negli estremi del moto la velocità è nulla ( il corpo si ferma per
tornare indietro ) e l’accelerazione è massima.
Prof. A. Di Muro
Considerando che v  ds
dt
si ha Acos  
d( A sen  )
d( A sen  )
d sen
da cui

 A
dt
d( t )
d
d sen 
d sen x
 cos  o più in generale
 cos x
d
dx
d( Acos  )
d( Acos  )
d cos 
dv
Analogamente a 
si ha 2 A sen  
da cui
 2
 2 A
dt
d( t )
d
dt
d cos 
d cos x
  sen  o più in generale
  sen x
d
dx
Abbiamo ricavato altre due regole di derivazione per il seno ed il coseno. 
Esercizio:
Un corpo si muove di moto armonico con un’ampiezza di oscillazione di 2.0 m. Sapendo che
all’istante t = 0 il corpo ha la massima velocità v  4.0 m / s determinare tutte le grandezze fisiche
del moto dopo 3.0 secondi.
Dalla v  Acos t si ha v  A  2.0  da cui   2.0 rad / s .
La posizione dopo 3 secondi è:
s  Asen t  2.0 sen 6.0  0.56 m
L’accelerazione è a  2 s  2.2 m / s 2
v
P

2
a
0
2
La velocità è v  Asen t  4.0 sen 6.0  1.1 m / s

La frequenza di oscillazione è  
 0.32 Hz
2
1
Il periodo dell’oscillazione è T   3.1 s . Il punto Q è nel terzo quadrante della circonferenza.

Esercizio:
Un corpo si muove di moto armonico con un’ampiezza di oscillazione di 3.0 m. In un certo istante
la sua accelerazione vale a =  12 m / s 2 e la sua velocità è negativa.
Sapendo che la frequenza è 2 /  Hz determinare tutte le grandezze fisiche del moto.
  2  4.0 rad / s
Accelerazione e velocità sono entrambe negative solo nel secondo quadrante, dalla terza equazione
del moto si ricava:
sen t  
a
12

 0.25 essendo nel secondo quadrante t    sen1 0.25  2.9 rad e
2
A
48
quindi t 
2.9
a
 0.72 s , lo spostamento è s   2  0.75 m , la velocità è


v  Acos t  12 cos 2.9  12 m / s