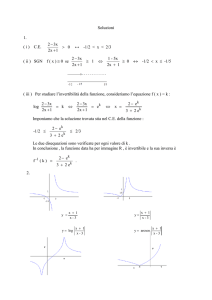
1. Funzioni implicite
1.1
Il caso scalare
Sia X ⊂ R2 e sia f : X → R. Una funzione y : (a, b) → R si dice definita implicitamente
dall’equazione f (x, y) = 0 in (a, b) quando:
1. (x, y(x)) ∈ X
2. f (x, y(x)) = 0
∀x ∈ (a, b);
∀x ∈ (a, b).
In generale una equazione in due variabili non definisce alcuna funzione implicita e, nel caso
in cui la definisca, non è detto che sia unica.
2
2
Esempio 1.1 Consideriamo
√ l’equazione f (x, y) = x + y − 4 = 0. La funzione y : [−2, 2] → R
definita dalla legge y(x) = 4 − x2 è funzione implicita relativa all’equazione f (x, y) = 0.
Esempio 1.2 L’equazione f (x, y) = x4 + y 4 = 0 non definisce alcuna funzione implicita.
Una condizione sufficiente affinchè una equazione definisca una funzione implicita è espressa dal
seguente
Teorema 1.1 (U.Dini) Sia Ω ⊆ R2 un aperto e sia f : Ω → R una funzione continua in Ω. Sia
P0 = (x0 , y0 ) ∈ Ω tale che f (P0 ) = 0, f è differenziabile in P0 e si abbia ∂f
∂y (P0 ) 6= 0. Allora,
∃ δ, k > 0 tali che nell’intervallo [x0 − δ, x0 + δ] si può definire almeno una funzione implicita
y : [x0 − δ, x0 + δ] → [y0 − k, y0 + k] relativa all’equazione f (x, y) = 0. Per ogni funzione y(x)
definita implicitamente si ha:
1. y(x0 ) = y0 ;
2. y(x) è continua in x0 ;
(P0 )
3. y(x) è derivabile in x0 e si ha: y 0 (x0 ) = − ffyx(P
0 ).
Dim. Per fissare le idee supponiamo che fy (x0 , y0 ) > 0. Allora, per definizione di derivata,
esiste k > 0 tale che
f (x0 , y)
>0
∀y ∈ [y0 − k, y0 + k], y 6= y0 .
y − y0
In particolare si ha f (x0 , y0 − k) < 0, f (x0 , y0 + k) > 0. Per il teorema di permanenza del segno è
possibile determinare δ > 0 tale che
f (x, y0 − k) < 0, f (x, y0 + k) > 0
∀x ∈ [x0 − δ, x0 + δ].
Per ogni x ∈ [x0 − δ, x0 + δ] sia y(x) una delle soluzioni dell’equazione f (x, y) = 0. Dalla costruzione
è evidente che ogni funzione y(x) definita implicitamente soddisfa la 1). Proviamo che verifica
anche la 2) della tesi. Dobbiamo provare che
∀ε > 0 ∃σ > 0 : |x − x0 | < σ ⇒ |y(x) − y0 | < ε
G.Di Fazio
ma questo è evidente se si osserva che è lecito prendere k ≤ ε. Per completare la dimostrazione
proviamo che ogni funzione definita implicitamente è differenziabile in x0 . Per il fatto che f è
differenziabile nel punto (x0 , y0 ) si ha:
f (x, y) = f (x0 , y0 ) + fx (x0 , y0 )(x − x0 ) + fy (x0 , y0 )(y − y0 ) + o(|x − x0 | + |y − y0 |).
Ponendo y = y(x) segue
y(x) = y0 −
fx (x0 , y0 )
(x − x0 ) + σ(x)(|x − x0 | + |y − y0 |), σ(x) → 0.
fy (x0 , y0 )
In un opportuno intorno di x0 si ha:
|y(x) − y0 | − |fy−1 (P0 )fx (P0 )(x − x0 )| ≤ |y(x) − y0 | − |fy−1 (P0 )fx (P0 )(x − x0 )|
≤ |y(x) − y0 − fy−1 (P0 )fx (P0 )(x − x0 )|
1
≤ σ(x)(|x − x0 | + |y − y0 |) ≤ (|x − x0 | + |y − y0 |)
2
e quindi,
1
1
|y(x) − y0 | ≤ |x − x0 | + |fy−1 (P0 )fx (P0 )(x − x0 )|
2
2
da cui
|y(x) − y0 | ≤ |x − x0 | 1 + 2|fy−1 (P0 )fx (P0 )| .
Allora, possiamo dire che
|y(x) − y0 + fy−1 (P0 )fx (P0 )(x − x0 )| = σ(x)(|x − x0 | + |y − y0 |)
≤ 2σ(x)|x − x0 |(1 + |fy−1 (P0 )fx (P0 )|) = o(|x − x0 |)
ovvero
quindi la tesi.
y(x) − y0
fx (x0 , y0 ) x − x0 + fy (x0 , y0 ) ≤ σ(x) → 0
Osservazione 1.1 Se l’ipotesi di differenziabilità vale in tutto Ω e se il differenziale è diverso da
zero in Ω allora la funzione implicita è unica e la formula di derivazione vale in tutto l’intervallo di
definizione. Infatti, nella costruzione precedente si ottiene che l’equazione f (x, y) = 0 ha una sola
soluzione y(x) per ogni x nell’intervallo considerato.
Il teorema precedente si estende al caso di funzioni di più variabili a valori reali.
Teorema 1.2 Sia Ω ⊆ Rn+1 un insieme aperto, (x0 , y0 ) ≡ (x0,1 , x0,2 , . . . , x0,n , y0 ) ∈ Ω e sia
f : Ω → R una funzione continua in Ω. Supponiamo che f (x0 , y0 ) = 0 e che f sia differenziabile nel
esistono δ, k > 0 in modo che l’equazione
punto (x0 , y0 ) e supponiamo risulti ∂f
∂y (x0 , y0 ) 6= 0. Allora,
Qn
f (x, y) = 0 definisce almeno una funzione implicita y : j=1 [x0,j − δ, x0,j + δ] → [y0 − k, y0 + k].
Per ogni funzione implicita si ha inoltre:
2
Appunti di Analisi Matematica II
1. y(x0 ) = y0 ;
2. y(x) è continua in x0 ;
3. y(x) è differenziabile in x0 e si ha:
∂y
∂xj (x0 )
=−
∂f
∂xj (x0 ,y0 )
∂f
∂yn (x0 ,y0 ).
Osservazione 1.2 Nel caso che la funzione implicita esiste ed è unica, dalla formula di derivazione
si deduce che, se la funzione f è di classe C k (Ω) allora la funzione implicita è di classe C k nel suo
campo di definizione.
1.2
Il caso vettoriale
Generalizziamo quanto visto per una sola equazione al caso di un sistema di equazioni.
Incominciamo generalizzando il concetto di derivata direzionale. Vogliamo derivare - piuttosto
che rispetto ad una direzione - rispetto ad un gruppo di direzioni indipendenti tra loro e cioè rispetto
allo spazio vettoriale generato da queste direzioni. Diciamo quindi v1 , . . . , vn le date direzioni ed
indichiamo con V lo spazio generato da v1 , . . . , vn .
Definizione 2.1 Sia f : Ω ⊆ Rn → Rm , x0 ∈ Ω e poniamo Ωx0 = {h ∈ V : x0 + h ∈ Ω}.
Diciamo che f è differenziabile nel punto x0 rispetto al sottospazio V = L(v1 , v2 , . . . , vp ) se la
funzione g(h) = f (x0 + h) : Ωx0 → Rm è differenziabile per h = 0. Conveniamo di indicare questo
∂f
differenziale con il simbolo ∂V
(x0 ).
Per conoscere il differenziale di f rispetto al sottospazio V bisogna conoscere il differenziale
della funzione g(h) = f (x0 + h) nel punto h = 0 che risulta quindi una matrice di tipo m × p.
Precisamente si tratta della matrice Jacobiana della funzione f rispetto alle direzioni che generano
V. Nel caso particolare che V = L(e1 , . . . , ep ) allora è la matrice Jacobiana della funzione f rispetto
alle variabili x1 , . . . , xp .
Esempio 2.1 Sia f : Ω ⊆ R4 → R2 , x0 ∈ Ω. Sia V = {t = 0} ≡ R3 . Differenziamo f rispetto a V.
Si ha: g 0 (0) : V → R2 ovvero g 0 (0) = Jg (0) ∈ R2,3 e quindi
∂f
(x0 ) = g 0 (0) =
∂R3
∂f1
∂x
∂f2
∂x
∂f1
∂y
∂f2
∂y
∂f1
∂z
∂f2
∂z
Dopo avere introdotto il concetto di derivata rispetto ad un sottospazio possiamo formulare la
generalizzazione del teorema della funzione implicita nel caso dei sistemi di equazioni.
Definizione 2.2 Sia f : Ω ⊂ Rn × Rm → Rn , con Ω insieme aperto in Rn × Rm . Data l’equazione
f (x, y) = 0 diciamo che y : A ⊆ Rn → Rm è una funzione implicita relativa all’equazione f (x, y) = 0
3
G.Di Fazio
se
1. (x, y(x)) ∈ Ω
2. f (x, y(x)) = 0
∀x ∈ A;
∀x ∈ A.
Enunciamo adesso e dimostriamo il teorema del Dini nel caso dei sistemi.
Teorema 2.1 Sia f : Ω ⊆ Rn ×Rm → Rn una funzione continua, (x0 , y0 ) ∈ Ω tale che f (x0 , y0 ) = 0.
∂f
Supponiamo la funzione f (x, y) differenziabile in (x0 , y0 ). Supponiamo ancora che ∂R
m (x0 , y0 ) sia
n
n
un isomorfismo di R in sè. Allora, esistono U intorno di x0 in R e V intorno di y0 in Rm tali
che si può definire almeno una funzione implicita relativa all’equazione f (x, y) = 0, y : U → V. Per
ogni funzione implicita definita dall’ equazione f (x, y) = 0 risulta:
1. y(x0 ) = y0 ;
2. y(x) è continua nel punto x0 ;
3. y è differenziabile in x0 e si ha: y 0 (x0 ) = −
∂f (x0 , y0 )
∂y
−1
◦
∂f (x0 , y0 )
∂x
Una importante applicazione di questo caso si ha in Meccanica Razionale riguardo ai parametri
Lagrangiani o gradi di libertà di un sistema fisico.
Esempio 2.2 Dato il sistema
x3 − 3xy 2 + z 3 + 1 = 0
x − 2y 2 − 3z 2 + 4 = 0
provare che y, z si possono esplicitare rispetto a x e poi, calcolare y 0 (1), z 0 (1).
Il problema si inquadra nel caso generale considerando la funzione
f : R × R 2 → R2
da cui
f (x, (y, z)) = (x3 − 3xy 2 + z 3 + 1, x − 2y 2 − 3z 2 + 4)
∂f
∂f
=
=
∂R2
∂(y, z)
−6xy
−4y
3z 2
−6z
Poichè il determinante della matrice è non nullo, si ha l’isomorfismo richiesto nell’ipotesi e quindi,
dal teorema del Dini segue la locale esplicitabilità. Per calcolare le derivate richieste basta derivare
membro a membro rispetto ad x le equazioni del sistema e poi valutarle nel punto x = y = z = 1.
Osservazione 2.1 Nel caso di un sistema lineare il teorema del Dini restituisce parzialmente il
4
Appunti di Analisi Matematica II
teorema di Rouchè - Capelli. Il vantaggio del teorema di Rouchè - Capelli è che fornisce risolubilità
globale. Lo svantaggio consiste nel fatto che il teorema di Rouché - Capelli si può applicare soltanto
al caso lineare.
Dimostriamo adesso il teorema.
Dim. Per semplicità possiamo supporre n = 2, m = 1. La dimostrazione si ripete inalterata
nella sostanza nel caso generale. Il sistema che vogliamo considerare si presenta dunque nella forma
seguente:
(
f1 (x, y1 , y2 ) = 0
f2 (x, y1 , y2 ) = 0
A causa dell’ipotesi sullo Jacobiano possiamo dire che, fissata una colonna del determinante - ad
esempio la prima - almeno uno dei complementi algebrici relativi agli elementi della colonna fissata
∂f1
(P0 ) 6= 0. Allora è possibile esplicitare
risulta diverso da zero. Supponiamo per esempio che sia ∂y
2
la variabile y2 dalla prima equazione cioè possiamo scrivere y2 = ϕ(x, y1 ) in un conveniente intorno
di x0 . Quindi, in un intorno di x0 abbiamo
(
y2 = ϕ(x, y1 )
f2 (x, y1 , y2 ) = 0
Verifichiamo adesso che nella seconda equazione è possibile esplicitare la variabile y1 . Per questo
basta garantire che
∂
f2 (x, y1 , ϕ(x, y1 )) 6= 0
∂y1
condizione senz’altro verificata grazie all’ipotesi sullo Jacobiano. Infatti, ponendo per comodità
F (y1 ) = f2 (x, y1 , ϕ(x, y1 )) si ha:
∂
∂f2 ∂x
∂f2 ∂y1
∂f2 ∂ϕ
F 0 (y1 ) = ∇f2 (x, y1 , ϕ(x, y1 )) ·
(x, y1 , ϕ(x, y1 )) =
+
+
∂y1
∂x ∂y1
∂y1 ∂y1
∂y2 ∂y1
!
∂f1
∂f2
∂f2
∂y
=
+
− ∂f11
∂y1
∂y2
∂y2
−1 −1 ∂f1 ∂f1 ∂y1 ∂y2 ∂f1
∂f1 ∂f2
∂f1 ∂f2
∂f1
∂f
6 0
=
−
=
2 ∂f2 =
∂y1
∂y2 ∂y1
∂y1 ∂y2
∂y1
∂y1
∂y2
In conclusione, in un conveniente intorno del punto x0 possiamo scrivere
(
y1 = ϕ1 (x)
y2 = ϕ2 (x)
che è quanto si voleva. Proviamo adesso la formula di derivazione. Dal fatto che f (x, y) è differenziabile nel punto (x0 , y0 ) si ha:
p
f (x, y) = f (x0 , y0 ) + Jf (x0 , y0 )(x − x0 , y − y0 )T + o( (x − x0 )2 + (y − y0 )2 )
e quindi, ponendo y = y(x) si ottiene:
p
0 = Jf (x0 , y0 )(x − x0 , y − y0 )T + o( (x − x0 )2 + (y − y0 )2 )
5
G.Di Fazio
Ricordando che la funzione f è una funzione di m + n variabili ad n componenti, il suo Jacobiano
è una matrice di tipo n × n + m cioè:
∂f1
∂x1
Jf (x0 , y0 ) = ...
∂fn
∂x1
da cui
Jf (x0 , y0 )(x − x0 , y − y0 )T =
∂f1
∂x2
...
∂fn
∂x2
...
∂f1
∂xm
∂f1
∂y1
∂fn
∂xm
∂fn
∂y1
...
...
∂f1
∂yn
∂fn
∂yn
∂f
∂f
(x0 , y0 )(x − x0 )T +
(x0 , y0 )(y − y0 )T
∂x
∂y
quindi,
0=
p
∂f
∂f
(x0 , y0 )(x − x0 )T +
(x0 , y0 )(y − y0 )T + o( (x − x0 )2 + (y − y0 )2 )
∂x
∂y
per cui, ricordando che det ∂f
∂y (x0 , y0 ) 6= 0, si ha;
T
y (x) =
y0T
−
−1 ∂f
∂f
(x0 , y0 )
(x0 , y0 ) (x − x0 )T + o(kx − x0 k).
∂y
∂x
Osservazione 2.2 Naturalmente vale quanto detto nel caso scalare e cioè che, se lo Jacobiano è
diverso da zero in tutto l’aperto allora la soluzione del sistema è unica.
Corollario 2.1 (Inversione locale) Sia f : Ω ⊆ Rn → Rn una funzione continua e differenziabile
nell’aperto Ω e supponiamo che in un punto x0 ∈ Ω si abbia f 0 (x0 ) 6= 0. Allora, f è localmente
invertibile in x0 ed inoltre, posto y0 = f (x0 ), si ha:
∂f −1
∂y
=
y0
∂f
∂x
−1
.
x0
Dim. basta applicare il teorema del Dini all’equazione F (x, y) = y − f (x). In particolare, posto
x = f −1 (y) si ha:
∂f −1
=−
∂x
6
∂F
∂x
−1
−1
−1
∂F
∂f
∂y
∂f
=− −
=
∂y
∂x
∂y
∂x
Appunti di Analisi Matematica II
1.3
Alcuni cambi di variabili
Come applicazione del teorema del Dini e dell’inversione locale studiamo alcuni cambi di variabile che saranno utili durante lo studio dell’ integrazione.
Esempio 3.1 Coordinate polari nel piano
Sia p : S0 → R2 \ L0 dove S0 =]0, +∞[×] − π, π[ e L0 = {(x, y) ∈ R2 : y = 0, x ≤ 0}. Posto
p(r, θ) = (x, y) = (r cos θ, r sen θ)
vogliamo studiare il problema dell’inversione di p. Si ha:
∂(x, y)
cos θ −r sen θ
=
sen θ r cos θ
∂(r, θ)
p
e quindi si ha esplicitabilità. Dalla definizione di p si ricava facilmente r = x2 + y 2 . La determinazione di θ è un pochino più laboriosa. Eseguendo i calcoli si ottiene θ(x, y) = arg(x, y)
dove:
y
x>0
arctang x
x
x < 0, y > 0;
arg(x, y) = − arctang y
arctang xy − π x < 0, y < 0.
Esempio 3.2 Coordinate cilindriche in R3
Consideriamo la funzione
k : R2 × R → R3
Si ha:
k(r, θ, ϕ) = (r cos θ, r sen θ, ϕ).
cos θ
∂(x, y, z)
= sen θ
∂(r, θ, ϕ)
0
−r sen θ
r cos θ
0
0
0
1
e si procede come nel caso delle coordinate polari nel piano.
Esempio 3.3 Coordinate polari in R3
Consideriamo la funzione
P :]0, +∞[×R × R → R3
Si ha:
P (r, θ, ϕ) = (r sen θ cos ϕ, r sen θ, sen ϕ, r cos θ).
sen θ cos ϕ r cos θ cos ϕ
∂(x, y, z)
= sen θ sen ϕ r cos θ sen ϕ
∂(r, θ, ϕ)
cos θ
−r sen θ
−r sen θ sen ϕ
r sen θ cos ϕ
0
e il determinante risulta r2 sen θ che è nullo soltanto se θ = kπ, k ∈ Z. Possiamo quindi considerare
una restrizione di P che può essere invertita. Precisamente, consideriamo
P :]0, +∞[×]0, π[×] − π, π[→ R3 \ {(x, 0, z) : x ≤ 0}
Sfruttando i risultati conseguiti negli esempi precedenti si ottiene:
P −1 : R3 \ {(x, 0, z) : x ≤ 0} →]0, +∞[×]0, π[×] − π, π[
P −1 (x, y, z) = (r, θ, ϕ) =
!
x
y
, arg(
,
)
sen θ sen θ
x2 + y 2 + z 2
p
x2 + y 2 + z 2 , arccos p
z
7