Corso di Studi in Fisica
Tutorato di Calcolo Differenziale ed Integrale
Esercizi proposti
Foglio 4 - Funzioni continue e funzioni derivabili
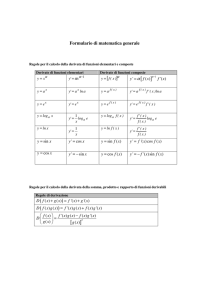
Esercizio 1.
Determinare i valori di α ∈ R, β ∈ (0, 1), per cui la funzione
eα(x−3) − 1
se x > 3
se x = 3
se x < 3
f (x) =
log(x − 2)
4
1
α − e + e 3−βx
è ovunque continua.
Esercizio 2.
Stabilire se le seguenti funzioni, definite e continue in R \ {0}, possono essere
prolungate per continuità su R. In caso affermativo, determinare il prolungamento e stabilire se è derivabile su R.
ex − 1
,
f (x) =
x
1
f (x) = e− x2 ,
1
f (x) = sin xe− x .
Esercizio 3.
Calcolare le derivate delle seguenti funzioni:
3.a) f (x) = 2x − 4x3
√
3.b) f (x) = xex
3.c) f (x) =
log x
x
3.d) f (x) = (log x)4
"
[2 − 12x2 ],
#
ex (1 + 2x)
√
,
2 x
"
#
1 − log x
,
x2
"
#
4(log x)3
.
x
Esercizio 4.
Stabilire in quali punti le seguenti funzioni risultano continue e in quali punti
risultano derivabili. Calcolare poi la derivata prima.
4.a) f (x) =
1
1−x
log x
(
2
se x ≤ 0
se 0 < x < 1
se x ≥ 1,
x2 + 2 se x < 0
cos x
se x ≥ 0.
4.b) f (x) =
Esercizio 5.
Determinare i valori di α ∈ R per cui la funzione
f (x) =
xα sin
0
1
x
se x > 0
se x ≤ 0
è ovunque differenziabile e calcolare, in tali casi, la derivata prima. Verificare
che, per α = 2, f è derivabile ma la derivata di f non è continua in x = 0.
Esercizio 6.
Determinare a, b ∈ R in modo che le seguenti funzioni siano continue su tutto
il loro insieme di definizione. Determinare poi i valori di a, b ∈ R tali che le
funzioni siano derivabili su tutto il loro insieme di definizione:
−x3 + ax + b se x < 0
ex
se x ≥ 0,
(
aex + bx + b se x ≥ 0
log(x + 2)3
se −2 < x < 0.
6.a) f (x) =
6.b) f (x) =
2
Esercizio 7.
Calcolare le derivate delle seguenti funzioni:
7.a) (x + x2 ) log x
x
7.b)
1 + x2
7.c) e−x (sin x + cos x)
7.d) (tan x)3
1−x
7.e) log
1+x
[log x(1 + 2x)
" + x + 1],
#
1 − x2
,
(1 + x2 )2
[−2e−x sin x],
[3 tan2 x(1 + tan2 x)],
2
,
x2 − 1
1
7.f) arctan
x
7.g) cosh(3x + 2)
1
7.h) x x
Esercizio 8.
Calcolare le derivate delle seguenti funzioni:
8.a) y = sin(3x2 + x + 1),
8.b) y = log(log2 (log x)),
3
8.c) y = 7(x +x+1) ,
8.d) y = sin2 (arctan
√ x), !
x2 − 1
,
8.e) y = arcsin5
x+1
1
8.f) y = e log x ,
8.g) y = arccos(tan(x2 + 1)),
8.h) y = log |x3 − 1|,
8.i) y = |(1 − x3 )1/3 − 1|.
1
−
,
1 + x2
[3"sinh(3x + 2)],
#
1 1 − log x
xx
.
x2