Gli integrali

Gli integrali
Come valutare somme di quantità variabili, estensioni di superfici, …?
Come trovare una funzione conoscendo la velocità con cui varia?
0. Introduzione
1. Calcolare l'area sotto al grafico di una funzione
2. La formula fondamentale del calcolo integrale
3. Alcuni esempi
4. Approfondimenti
5. Esercizi
Sintesi
0. Introduzione
In questa scheda affronteremo due problemi:
– come calcolare l'area di una figura a contorno non poligonale, generalizzando idee e tecniche messe a punto
nella prima scheda sulle figure piane,
– come trovare una funzione conoscendo il modo in cui varia (leggendo al passare del tempo il tachimetro di
un'automobile - se il contachilometri è rotto - come posso calcolare la quantità di strada via via percorsa?).
Sono problemi apparentemente lontani, ma vedremo (affrontando il cosiddetto "teorema fondamentale")
come essi siano invece strettamente collegati.
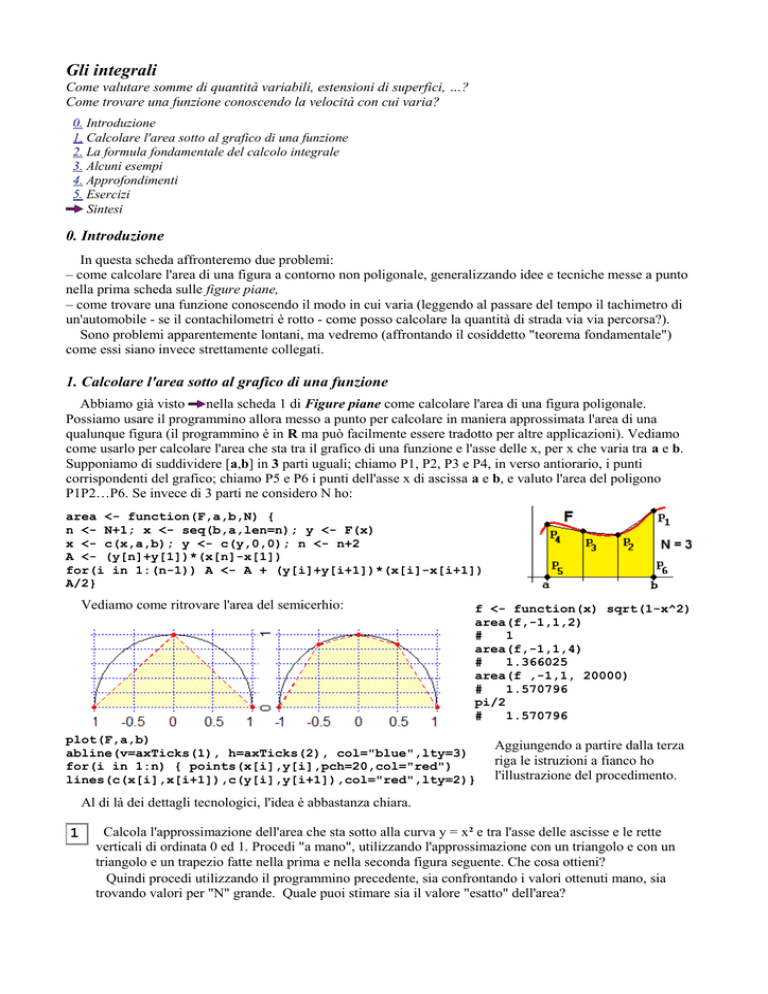
1. Calcolare l'area sotto al grafico di una funzione
Abbiamo già visto nella scheda 1 di Figure piane come calcolare l'area di una figura poligonale.
Possiamo usare il programmino allora messo a punto per calcolare in maniera approssimata l'area di una
qualunque figura (il programmino è in R ma può facilmente essere tradotto per altre applicazioni). Vediamo
come usarlo per calcolare l'area che sta tra il grafico di una funzione e l'asse delle x, per x che varia tra a e b.
Supponiamo di suddividere [a,b] in 3 parti uguali; chiamo P1, P2, P3 e P4, in verso antiorario, i punti
corrispondenti del grafico; chiamo P5 e P6 i punti dell'asse x di ascissa a e b, e valuto l'area del poligono
P1P2…P6. Se invece di 3 parti ne considero N ho:
area <- function(F,a,b,N) {
n <- N+1; x <- seq(b,a,len=n); y <- F(x)
x <- c(x,a,b); y <- c(y,0,0); n <- n+2
A <- (y[n]+y[1])*(x[n]-x[1])
for(i in 1:(n-1)) A <- A + (y[i]+y[i+1])*(x[i]-x[i+1])
A/2}
Vediamo come ritrovare l'area del semicerhio:
f <- function(x) sqrt(1-x^2)
area(f,-1,1,2)
#
1
area(f,-1,1,4)
#
1.366025
area(f ,-1,1, 20000)
#
1.570796
pi/2
#
1.570796
plot(F,a,b)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
for(i in 1:n) { points(x[i],y[i],pch=20,col="red")
lines(c(x[i],x[i+1]),c(y[i],y[i+1]),col="red",lty=2)}
Aggiungendo a partire dalla terza
riga le istruzioni a fianco ho
l'illustrazione del procedimento.
Al di là dei dettagli tecnologici, l'idea è abbastanza chiara.
1
Calcola l'approssimazione dell'area che sta sotto alla curva y = x² e tra l'asse delle ascisse e le rette
verticali di ordinata 0 ed 1. Procedi "a mano", utilizzando l'approssimazione con un triangolo e con un
triangolo e un trapezio fatte nella prima e nella seconda figura seguente. Che cosa ottieni?
Quindi procedi utilizzando il programmino precedente, sia confrontando i valori ottenuti mano, sia
trovando valori per "N" grande. Quale puoi stimare sia il valore "esatto" dell'area?
La figura a lato illustra il caso di una funzione definita in un intervallo che è
l'unione di intervallini su cui la funzione è continua; è la funzione parte intera, ma
potrebbe essere anche un'altra funzione, a patto che sia limitata (ossia non abbia
asintoti verticali). Anche in questi casi il procedimento fornisce il valore giusto.
2
Calcola a mano l'area che sta tra la curva y = floor(x) e l'asse x per x
compreso tra 0 e 3. Qual è il valore che il programma precedente fornisce per
N = 2? Verifica che per N che cresce si ottiene un valore che si avvicina
sempre più all'area effettiva.
A lato sono rappresentati, al variare delle ascisse tra
−1 ed 1, i grafici di f1 e f2. Se uso il programma
precedente per valutare le aree tra essi e l'asse x
ottengo, rispettivamente, 4/3 e −4/3. Infatti il
programma calcola le aree orientate: positive se
stanno sopra all'asse x, negative se stanno sotto ad
esso. Le "aree" delle due superfici sono invece
entrambe positive.
f1 <- function(x) -x^2+1
f2 <- function(x) -f1(x)
area(f1, -1,1, 5000)
#
1.333333
area(f2, -1,1, 5000)
#
-1.333333
3
Sia h la funzione rappresentata graficamente a fianco.
(1) Quanto vale, per un generico input x, h(x)?
(2) Secondo te quanto vale l'area orientata tra il grafico di h e l'asse x
(al variare dell'input tra −2 e 2)?
(3) Controlla la risposta usando il programma illustrato in precedenza.
In tutti questi casi, dato un intervallo finito [a,b] e una funzione F che sia continua in [a,b], o che sia ivi
limitata e continua in intervalli la cui unione sia [a,b], l'area orientata tra grafico di F ed asse x viene chiamata
integrale di F tra a e b e indicata ∫[a,b] F o ∫ab F, o, per comodità, a ∫ b F.
Se la funzione F è descritta esplicitamente si usa una notazione in cui compare un nome per la variabile. Ad
esempio nel primo esempio posso scrivere −1 ∫ 1 √(1-x²) dx (o −1 ∫ 1 √(1-u²) du o …).
Il simbolo ∫ ha la forma di una "S" allungata. Infatti ricorda che l'area che sta sotto alla curva può essere
approssimata sommando opportuni trapezi.
4
Quanto valgono −1 ∫ 1 s² − 1 ds e 0 ∫ 2 x dx? (nota: non serve racchiudere s²−1 tra parentesi in quanto
c'è ds che delimita dove finisce l'espressione da integrare)
5
Quanto vale −π ∫ π sin ?
(congettura quello che dovrebbe valere e usa il
programma per controllare la tua risposta − a lato è
illustrato quello che accade per N=4)
Quanto vale 0 ∫ π sin ?
6
La figura seguente illustra due proprietà degli integrali, simili a proprietà che abbiamo visto per le derivate,
che useremo spesso (k è un numero reale):
∫ [a, b] (F+G) = ∫ [a, b] F + ∫ [a, b] G
∫ [a, b] (k F) = k ∫ [a, b] F
2. La formula fondamentale del calcolo integrale
Costruire approssimazioni successive, man mano più precise, è un operazione comoda per calcolare singoli
integrali, se si dispone di un computer. Vedremo in questo paragrafo che in molte situazioni si può ricorrere ad
un metodo più semplice, che ci consente di valutare gli integrali utilizzando opportune formule. Nel paragrafo
"approfondimenti" faremo qualche considerazione storica sull'origine di questo metodo.
Illustriamo il metodo con un esempio. Consideriamo la funzione x → m·x. Sotto a sinistra ne è rappresentato
il grafico. Vediamo come determinare l'area della figura illustrata sotto a destra, ossia ∫ab mx dx, con una
formula.
L'area tra grafico ed asse orizzontale che va dall'ascissa 0 all'ascissa x è quella di un triangolo con base x ed
altezza m·x, cioè 1/2·m·x². Quella che va dall'ascissa a all'ascissa b è, evidentemente, la differenza tra l'area
del triangolo BOK e quella del triangolo AOH: 1/2·m·b²−1/2·m·a².
Ma Dx (1/2·m·x²) = m·x, ovvero 1/2·m·x² è un'antiderivata (rispetto ad x) di m·x.
In definitiva ∫ab mx dx = F(b)−F(a), dove F è un'antiderivata di x → m·x (il concetto di antiderivata, o
primitiva, di una funzione è stato introdotto alla fine del §3 della scheda sulla
derivazione).
La cosa potrebbe essere dimostrata in generale:
sia f continua in [a, b]; se G' = f allora
∫ [a, b] f = G(b) − G(a)
Questa proprietà viene chiamata formula fondamentale del calcolo integrale.
Usa la formula fondamentale del calcolo integrale per calcolare l'area compresa tra y = x², l'asse x e le
rette x=0 ed x=1 (qual è la più semplice antiderivata che puoi usare? come sono fatte le altre?). Ritrovi il
valore trovato affrontando il quesito 1?
7
Calcola l'area compresa tra y = x², l'asse x e le rette x=−1 ed x=1.
8
Confronta l'area che hai calcolato nel quesito 3 con il valore che ottieni usando la formula fondamentale
del calcolo integrale.
9
Possiamo ora osservare come i due problemi illustrati nel
10
Rileggete §0 e spiegate questa osservazione ...
§0 sono collegati.
3. Alcuni esempi
Vediamo come si potrebbero calcolare gli integrali con R (rivediamo i calcoli svolti dopo il
quesito 2):
g <- function(x) -x^2+1
integrate(g, -1,1)
# 1.333333 with absolute error < 1.5e-14
integrate(g, -1,1)$value
# 1.333333
library(MASS); fractions( integrate(g,-1,1)$value )
# 4/3
e con WolframAlpha: digitando integrate -x^2+1 from x=-1 to 1 ottieni 4/3.
Accenniamo a due esempi tipici di impiego della integrazione definita, che si affiancano a quello del calcolo
delle aree.
Il primo si riferisce alla fisica. Consideriamo un problema simile a quello discusso all'inizio di
§2. Un
oggetto si muove con velocità v che cresce linearmente col tempo t, ossia con accelerazione costante a (se a =
dv/dt è costante, v = a·t). Ecco, sotto, a sinistra, il grafico di v in funzione di t.
Se la velocità fosse costante avremmo il grafico al centro, con v = s/Δt, dove s è lo spazio percorso, e questo
sarebbe uguale a v·Δt, ossia all'area del rettangolo raffigurato (con Δt abbiamo indicato t2 − t1).
Se v varia s è pari all'area di forma diversa che viene descritta dal segmento verticale che congiunge l'asse x
ed il grafico di v con ascissa che varia da t1 a t2 , ossia a ∫ [t1, t2] v.
Il secondo esempio si riferisce al calcolo delle probabilità. Se hai già affrontato lo studio delle variabili
casuali continue puoi approfondire l'argomento. Altrimenti ti limiti a leggere i seguenti commenti, su cui potrai
tornare sopra in un secondo momento.
Per brevità facciamo i calcoli con R. Viene descritta una funzione F; viene verificato che, nell'intervallo [0,3], è
una funzione di densità, ossia che l'area sottesa al suo grafico per le ascisse comprese tra 0 e 3 vale 1; ne viene
tracciato il grafico; viene calcolata la sua media, ossia l'integrale della funzione G sotto definita; viene infine
tracciata la retta verticale avente per ascissa il valor medio.
F <- function(x) (x/3-1)^2
integrate(F, 0,3)$value
# 1
plot(F, 0,3)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
G <- function(x) x*F(x)
m <- integrate(G, 0,3)$value; m
# 0.75
abline(v=m,col="red")
4. Approfondimenti
Se hai già affrontato lo studio della derivazione delle funzioni sin e cos (nel §7 della scheda di avvio alla
derivazione) puoi anche studiare come determinarne le antiderivate. Infatti abbiamo visto che D(sin) = cos e
che D(cos) = −sin, come puoi facilmente ricordare pensando ai loro grafici:
11
Qual è l'antiderivata di cos? Quanto vale ∫ [0,π/2] cos?
Qual è l'antiderivata di sin? Quanto vale ∫ [0,π/2] sin?
Se hai già affrontato lo studio della derivazione della funzione esponenziale (nel §8
della scheda di avvio alla derivazione) puoi anche studiare come determinarne le
antiderivate. Infatti abbiamo visto che D(exp) = exp.
12
Qual è l'antiderivata di exp? Stima dal grafico quanto vale ∫ [0,1] exp.
Calcola quanto vale ∫ [0,1] exp. Calcola quanto vale ∫ [−1,0] exp. Calcola quanto
vale ∫ [−1,1] exp.
Facciamo, infine, qualche richiamo storico.
Le origini del concetto di integrazione sono molto antiche. Vari metodi per il calcolo esatto di aree
di particolari figure a contorno curvilineo basati sulla loro approssimazione mediante figure poligonali
erano già note alcuni secoli a.C. (Eudosso, Archimede, …). Furono poi estese ad altre figure, grazie ad
una prima introduzione delle coordinate, da Oresme, intorno al 1350 e, successivamente, da altri
studiosi, tra cui Galileo, Torricelli e Cavalieri (sono tutte persone che, come abbiamo già ricordato,
non erano dei matematici di professione, ma si occupavano di filosofia, tecnica, economia, scienze,
arte, …: la matematica come disciplina autonoma risale al XIX secolo).
La scoperta della formula fondamentale del calcolo è dovuta, intorno al 1670, a Newton e Leibniz.
5. Esercizi
e1
Traccia (usando il computer) il grafico di x → (10*x-5)/(x^2+1) ristretta al dominio [1/2,3]. Valuta
graficamente il valore del suo integrale su tale intervallo. Calcola, infine, tale integrale arrotondato a 7
cifre.
e2
Calcola, arrotondati a 7 cifre, l'integrale tra −1 e 0 e tra −1 e 3 della stessa funzione del quesito e1.
e3
Quanto vale l'integrale di floor tra 0 e 5? E quello tra -2 e 5?
e4
Sia F la funzione così definita: F(x) = x. Quali sono tutte le antiderivate di F?
e5
Sia F la funzione così definita: G(x) = x+2. Quali sono tutte le antiderivate di G?
e6
Trova l'antiderivata più semplice per le seguenti funzioni, che ad x associano:
2 x, k x, x², 2 x², k x², 5 x + 1, 3 x² − 2 x + 2
e7
Se hai studiato la parte di §4 relativa alle funzioni circolari, calcola l'antiderivata rispetto ad x di:
cos(x) + 1, cos(3 x), x² + cos(2 x), 3 sin(x), 3·sin(3 x)
e8
Se hai studiato la parte di §4 relativa alla funzione esponenziale, calcola l'antiderivata rispetto ad x di:
5 ex, e3 x, x³ + 4 ex/5
e9
Calcola (e fai uno schizzo del grafico per valutare la ragionevolezza del risultato):
1
2
1
2
1
5
0 ∫ 2x dx, 1 ∫ 2x dx, −1 ∫ 2x dx, −2 ∫ 2x dx, 0 ∫ 3x dx, −5 ∫ 3x dx,
0∫
2 x²
dx,
−2 ∫
2 x²
dx,
0∫
2 x³
dx,
−2 ∫
2 x³
dx,
0∫
2 2x²−3x+1
dx
e10
Se hai studiato la parte di §4 relativa alle funzioni circolari, calcola (e fai uno schizzo del grafico per
valutare la ragionevolezza del risultato):
π
π/2 sin(x) dx,
π
π/2 cos(x) dx,
0 ∫ sin(x) dx, −π/2 ∫
0 ∫ cos(x) dx, −π/2 ∫
−π/2 ∫
e11
π/2 cos(2x)
dx,
0∫
π/3 sin(3x)
dx,
0∫
π/5 sin(5x)
dx,
0∫
π sin(x)+cos(x)
dx
Se hai studiato la parte di §4 relativa alla funzione esponenziale, calcola (e fai uno schizzo del
grafico per valutare la ragionevolezza del risultato):
1 x
2 x
2 x
2 x+1 dx
0 ∫ e dx, 0 ∫ e dx, 0 ∫ e +1 dx, 0 ∫ e
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato
dei seguenti termini:
area orientata (§1), integrale di una funzione (§1), formula fondamentale del calcolo integrale (§2)
2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati
mediante una frase in cui esso venga impiegato.
3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono")
il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").