Affinità parte seconda
Pagina 8 di 5
easy matematica di Adolfo Scimone
Omotetia
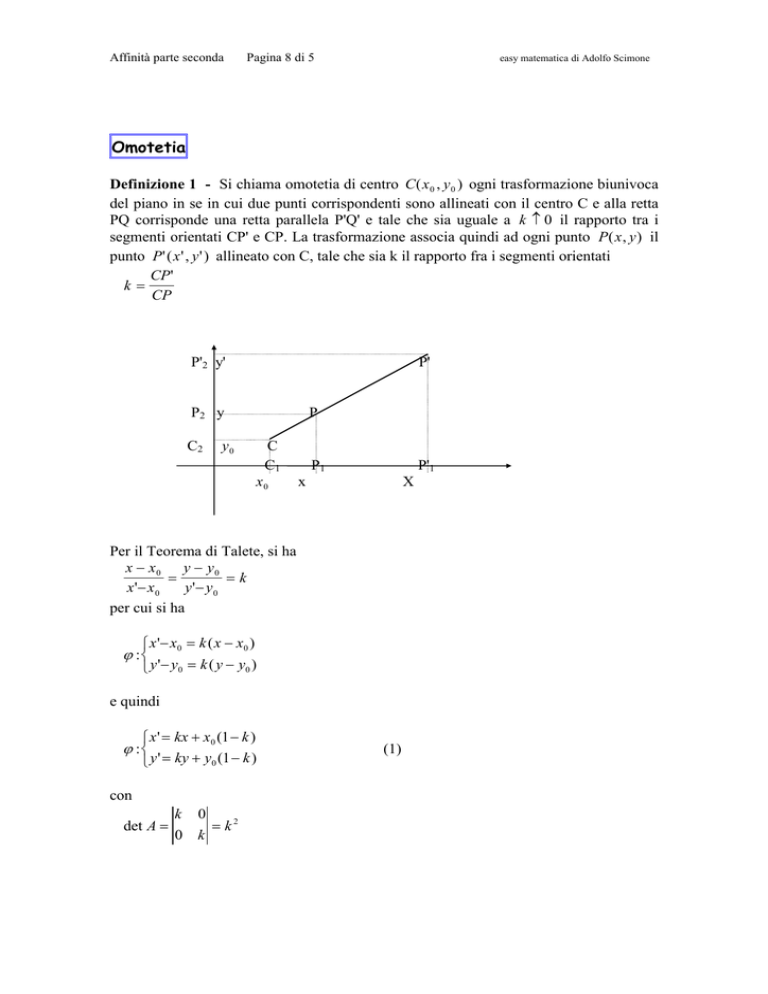
Definizione 1 - Si chiama omotetia di centro C ( x 0 , y 0 ) ogni trasformazione biunivoca
del piano in se in cui due punti corrispondenti sono allineati con il centro C e alla retta
PQ corrisponde una retta parallela P'Q' e tale che sia uguale a k ≠ 0 il rapporto tra i
segmenti orientati CP' e CP. La trasformazione associa quindi ad ogni punto P( x , y ) il
punto P'( x ' , y ' ) allineato con C, tale che sia k il rapporto fra i segmenti orientati
CP'
k=
CP
P'2 y'
P'
P2 y
C2
P
C
C1
y0
x0
P1
P'1
x
X
Per il Teorema di Talete, si ha
x − x0 y − y0
=
=k
x '− x 0
y '− y 0
per cui si ha
x ' − x0 = k ( x − x0 )
y ' − y0 = k ( y − y0 )
ϕ :
e quindi
x ' = kx + x0 (1 − k )
y ' = ky + y0 (1 − k )
ϕ :
con
det A =
k
0
0 k
= k2
(1)
Affinità parte seconda
Pagina 9 di 5
easy matematica di Adolfo Scimone
Il punto C ( x 0 , y 0 ) è il punto unito della trasformazione e si chiama centro
dell'omotetia ; ogni retta passante per C viene trasformata in se stessa : è perciò una retta
unita.
Dicesi affinità omologica ogni affinità avente una retta luogo di punti fissi (asse) tale
che le congiungenti punti corrispondenti sono tra loro parallele (direzione) e rette
corrispondenti si intersecano sull’asse.
L’affinità omologica si dirà ortogonale se la sua direzione è perpendicolare all’asse.
Teorema - Ogni omotetia è una similitudine di rapporto | k | ;
se | k | > 1 si ha una dilatazione ;
se 0 < | k | < 1 si ha una contrazione
se k = 1 si ha l'identità
se k = -1 si ha la simmetria centrale di centro C.
Si dimostra che il rapporto fra le aree di due figure corrispondenti F e F' è uguale al
quadrato della costante di omotetia.
Definizione 2 - L'omotetia (1) si dice concorde se k ∈ R +
Essa trasforma un segmento PQ nel segmento P'Q' parallelo ed equiverso al primo.
Q'
Q
P
P'
C
Definizione 3 - L'omotetia (1) si dice discorde o inversa se k ∈ R −
Essa trasforma un segmento PQ nel segmento P'Q' parallelo e di verso opposto a PQ
Q
P
C
Q'
P'
Affinità parte seconda
Pagina 10 di 5
easy matematica di Adolfo Scimone
Se il centro dell'omotetia è l'origine, la trasformazione ha equazioni
x ' = kx
y ' = ky
ϕ :
(2)
che trasformano un punto P( x , y ) nel punto P' ( kx , ky ) e ai punti (1, 0) e (0, 1)
corrispondono i punti (k , 0) e (0, k ) per cui le (2) rappresentano un cambiamento di
unità di misura per i segmenti del piano se k è positivo, ; se k è negativo rappresentano
anche un cambiamento del senso positivo degli assi del sistema.
Rotomotetie
Definizione 4 - Si chiama rotomotetia di centro O, di angolo α e costante k ≠ 0 , la
trasformazione del piano in se di equazioni
x ' = k ( x cos α − y sen α )
y ' = k ( x sen α + y cos α )
ϕ :
(3)
Se k = 1 si ha una rotazione di ampiezza α , mentre se α = 0 non si ha un'omotetia.
La (3) si può pensare quindi come la trasformazione che muta un segmento PQ nel
segmento corrispondente P'Q' che rispetto al primo risulta ruotato di un angolo α e k
volte dilatato.
Teorema - Ogni similitudine di centro O è una rotomotetia, o in particolare una
omotetia o una rotazione.
Sia data una similitudine concorde
x ' = a11 x −12 y
y ' = a12 x + a11 y
ϕ :
Essendo
a112 + a122 = k 2
possiamo porre
a11 = k cos α
per cui si ha
a12 = k sen α
x ' = kx cos α − ky sen α
y ' = kx sen α + ky cos α
ottenendo la (3).
Si dimostra che una rotomotetia propria ha un solo punto unito, detto centro e nessuna
retta unita.
ϕ :
Affinità parte seconda
Pagina 11 di 5
easy matematica di Adolfo Scimone
ISOMETRIE
Definizione 1 - Si chiama isometria una trasformazione del piano in sé che conserva le
distanze, ossia se P'Q' è il segmento corrispondente di PQ nella trasformazione, si ha
d ( P, Q) = d ( P' , Q' ) ∀P, Q ∈R 2
per cui un'isometria è una particolare similitudine di rapporto k = 1, perciò un'isometria
conserva anche gli angoli ed è individuata dalle equazioni
x ' = a11 x − a12 y + p
y ' = a12 x + a11 y + q
ϕ :
x ' = x cos α − y sen α + p
o ϕ :
y ' = x sen α + y cos α + q
con det A = 1, detta anche isometria diretta o concorde, o congruenza.
Le congruenze conservano gli orientamenti delle figure, sono, cioè trasformazioni
concordi.
Oppure:
x ' = a11 x + a12 y + p
y ' = a12 x − a11 y + q
ϕ :
x ' = x cos α + y sen α + p
o ϕ :
y ' = x sen α − y cos α + q
con det A = - 1, detta anche isometria inversa o indiretta o discorde.
Osservazione
Se una isometria concorde non è una traslazione, né una simmetria centrale sarà una
rotazione il cui centro (punto unito) si trova sugli assi dei segmenti AA’ e BB’
Una isometria discorde è una simmetria ortogonale se i vettori AA' e BB' sono
paralleli:
AA' // BB'
Una isometria discorde, se non è una simmetria ortogonale sarà il prodotto di una
simmetria ortogonale per una traslazione o rotazione.
Si osservi che affinchè una affinità sia un’isometria, la matrice della trasformazione
deve essere ortogonale, ossia
A ⋅ t A= t A ⋅ A = I n
L’insieme delle isometrie di uno spazio E è un gruppo rispetto al prodotto. La geometria
che esso definisce è la geometria metrica.
Le isometrie, ovvero quelle particolari trasformazioni biunivoche del piano in sé che
conservano le distanze e gli angoli, si classificano in
1) identità
2) traslazioni
3) rotazioni
4) rototraslazioni
5) simmetrie centrali e assiali
Affinità parte seconda
Pagina 12 di 5
easy matematica di Adolfo Scimone
1) Identità L'dentità ha equazioni
x' = x
y' = y
nell'identità tutti i punti sono uniti.
ϕ :
2) Traslazione Dicesi traslazione ogni isometria diretta nella quale se A' e B' sono i
corrispondenti di due punti qualsiasi A e B, rispettivamente si ha
d ( A, A' ) = d ( B , B ' )
le equazioni sono pertanto
x' = x + p
y' = y + q
ϕ :
Nella traslazione , che non sia l'identità, non vi sono punti uniti.
3) Rotazione Si dice rotazione di un piano, di centro un punto O e di ampiezza un
angolo α, la corrispondenza che ad O associa O stesso e ad ogni punto P ∈R 2 associa
P' ∈R 2 tale che
d ( O, P ) = d ( O, P ' )
∧
e l'angolo orientato P O P' sia congruente e concorde ad α.
Le equazioni della rotazione attorno all'origine sono
x ' = x cos α − y sen α
ϕ :
rotazione diretta
y ' = x sen α + y cos α
oppure
x ' = x cos α + y sen α
rotazione inversa
y ' = x sen α − y cos α
Nella rotazione il punto O è punto unito.
Se α = π si ha la simmetria rispetto ad O(0, 0) di equazioni
x' = − x
ϕ :
y' = − y
ϕ :
Se α = 0 si ha x = x' e y = y' che rappresentano la trasformazione identica I, in cui ogni
punto del piano è punto unito.
Una rotazione di centro C ( xC , yC ) ed ampiezza α ha equazioni:
x'− xC = ( x − xC ) cos α − ( y − yC ) sen α
y '− yC = ( x − xC ) sen α + ( y − yC ) cos α
ϕ:










