Integrale
Il concetto d’integrale nasce per risolvere due classi di
problemi:
Integrale Definito
Integrale Indefinito
• Calcolo delle aree di figure delimitate
da curve
• calcolo di volumi
• calcolo del lavoro di una forza
• calcolo dello spazio percorso …..
• Problema inverso del calcolo della
derivata:
nota la derivata di una funzione
calcolare la funzione stessa.
1
Calcolo delle Aree
Area dei poligoni:
È la situazione più semplice in quanto qualunque
poligono può essere scomposto in triangoli e la sua
area ricondotta all’area di un rettangolo equivalente.
Area del Rettangolo
A=b•h
Basta ricoprire la superficie
del rettangolo con quadratini
di area unitaria
2
Poligoni regolari
Scomponendoli in triangoli congruenti è facile
calcolare l’area
Area di un Esagono
Atriangolo
l⋅a
=
2
a⋅l
a ⋅ l ⋅ n a ⋅ (l ⋅ n) a ⋅ p
⋅n =
=
=
Apoligono=
2
2
2
2
a
l
3
Poligoni Irregolari
Basta scomporli opportunamente in triangoli
Area di un Poligono qualsiasi
A poligono =
n
∑ Atriangoli
1
4
Area del Cerchio
Il calcolo dell’area è molto più complesso in quanto
non è possibile scomporre il cerchio in triangoli.
E’ possibile però calcolare l’area per approssimazioni
successive:
Indichiamo con A la classe dei poligoni regolari inscritti nel cerchio,
di 3, 4, 5, 6, n lati rispettivamente
e con a3, a4, a5, … an le relative aree;
e con B la classe dei poligoni regolari circoscritti al cerchio
di 3, 4, 5, 6, …n lati
e con b3, b4, b5, bn le rispettive aree.
Se S è l’area del cerchio (incognita) sarà sempre:
an ≤ S ≤ bn
5
e passando al limite di infiniti lati :
lim an = lim bn = S = Area Cerchio
n →+∞
n →+∞
Allora: L’area del cerchio è uguale al limite comune,
quando il numero lati ∞, al quale tendono le successioni
formate dalle aree dei poligoni inscritti e circoscritti al
cerchio
6
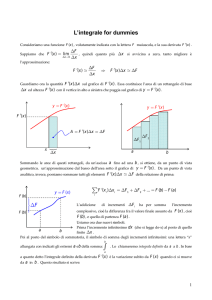
Area del Trapezoide
Vogliamo calcolare l’area della figura mistilinea
determinata dal diagramma di una funzione y = f(x)
definita e continua nell’intervallo [a, b]
y
C
D
A
B
a
b
x
7
Possiamo determinare l’area approssimandola con
dei rettangoli inscritti e dei rettangoli circoscritti
Utilizzando lo stesso metodo usato per il cerchio.
Dividendo in n parti
l’intervallo [a, b], avremo n
rettangoli di base
h = (b – a)/n
y
C
Indichiamo con
sn = Σ areaRett.inscritti
D
A
L’area del plurirettangolo
inscritto
B
a
b
x
8
Analogamente possiamo determinare l’area Sn del
plurirettangolo circoscritto
Indichiamo con
Sn = Σ areaRett.circoscritti
y
C
D
A
B
a
b
x
L’area S del trapezoide sarà sempre compresa tra sn e Sn
Σ areaRett.inscritti ≤ S ≤ Σ areaRett.circoscritti
9
Aumentando il numero dei rettangoli
l’approssimazione di S sarà sempre più precisa.
Considerando un numero di rettangolini via via crescente
avremo due successioni di aree di
plurirettangoli inscritti
s1, s2, … sn, … e di
plurirettangoli circoscritti
S1, S2, …Sn,…
che convergono all’area del trapezoide ABCD
Teorema 1. Se y = f(x) è continua e positiva in [a, b], allora le
successioni delle aree s1, s2, … sn, … e S1, S2, …Sn,…
convergono allo stesso limite S uguale all’area del trapezoide
ABCD
lim s n = lim S n = S
n → +∞
n → +∞
10
Possiamo finalmente giungere al concetto d’integrale definito
Integrale Definito
Data la funzione y=f(x) definita e continua in [a, b],
dopo aver diviso l’intervallo in n parti, indichiamo con
mi = min f(x) e con Mi = max f(x) nell’intervallino i-esimo di
ampiezza h
ARettcirco. = Mi•h
ARettinscr. = mi•h
y
C
Mi
D
sn =AreaPluriRettinscr. = Σ mi•h
Sn =AreaPluriRettcirco. = Σ Mi•h
mi
A
a
i
h
B
b
x
11
Allora,indicando con f(εi ) il valore della funzione in un punto
qualsiasi dell’intervallo i-esimo,
tenendo conto del teorema del confronto e del teorema 1
mi ≤ f (εi ) ≤ Mi
∑m ≤∑ f (ε ) ≤ ∑M
y
i
Mi
D
i
∑m ⋅ h ≤∑ f (ε ) ⋅ h ≤ ∑M ⋅ h
C
i
i
i
f(εi )
lim ∑mi ⋅ h = lim ∑Mi ⋅ h =S
mi
n→+∞
A
B
εi
a
i
b
n→+∞
avremo che:
x
lim ∑mi ⋅ h = lim ∑Mi ⋅ h = lim ∑ f (εi ) ⋅ h =S
n→+∞
n→+∞
n→+∞
12
Allora, possiamo dare la seguente definizione:
Def. Data la funzione y=f(x) definita e continua in [a, b],
si dice Integrale definito di f(x) relativo all’intervallo [a, b] il
limite
lim ∑mi ⋅ h = lim ∑Mi ⋅ h = lim ∑ f (εi ) ⋅ h =S
n→+∞
n→+∞
n→+∞
b
e si indica con
∫
f ( x ) dx
a
13
Proprietà dell’Integrale definito
b
a)
a
a
∫ f (x)dx = −∫ f (x)dx
a
∫ f (x)dx = 0
b)
b
a
Proprietà di linearità
c)
d)
b
b
a
a
∫ kf ( x ) dx = k ∫ f ( x ) dx
b
b
b
a
a
a
∫ [ f ( x ) + g ( x ) ]dx = ∫ f ( x ) dx + ∫ g ( x ) dx
Proprietà di additività
b
e)
∫
a
c
f ( x ) dx =
∫
a
b
f ( x ) dx +
∫
f ( x ) dx
c
14
Teorema della Media
Se y = f(x) è una funzione continua nell’intervallo
chiuso e limitato [a, b] allora esiste almeno un punto
c∈(a, b) tale che:
b
∫ f ( x)dx = (b − a) f (c)
a
y
f(c)
f(c)
Cioè esiste sempre un
rettangolo di base AB e
altezza uguale a f(c) avente la
stessa area del rettangoloide.
C
D
A
c
a
B
c
b
x
15
Funzione Primitiva
Il calcolo dell’integrale come lim Σ è estremamente
complesso e per nulla conveniente, occorre allora trovare un
altro sistema per calcolarlo.
Abbiamo bisogno di vedere il concetto di primitiva e il
teorema di Torricelli-Barrow
Il problema del calcolo della Primitiva è il problema
inverso del calcolo della derivata:
calcolare la primitiva significa:
data la derivata f(x) di una certa funzione non nota F(x)
calcolare la funzione y=F(x),
quindi F’(x) = f(x)
16
Derivata
F(x)
?
f(x)
Primitiva
Def. Diremo che F(x) è una primitiva della funzione
y=f(x) in [a, b]
sse
F(x) è derivabile in [a, b] e risulta:
F’(x) = f(x)
∀ x ∈[a, b]
17
Primitive, alcuni esempi:
Primitiva (2x) = x2
--- infatti → D(x2) = 2x
Primitiva (cosx) = senx
--- infatti → D(senx) = cosx
Primitiva (1/x) = lnx
--- infatti → D(lnx) = 1/x
Primitiva (1/cos2x) = tgx
--- infatti → D(tgx) = 1/cos2x
Osserviamo anche che:
D(x2-1) = 2x --- quindi → Primitiva (2x) = x2 –1
D(x2+5) = 2x --- quindi → Primitiva (2x) = x2 +5
D(x2+a) = 2x --- quindi → Primitiva (2x) = x2 +a
18
Oss
Se F(x) è una primitiva di f(x) allora
anche
G(x) = F(x) + c ∀ c ∈R è una primitiva di f(x)
e viceversa
se F(x) e G(x) sono primitive di f(x) allora
G(x) = F(x) + c
Allora una funzione ammette infinite primitive che
differiscono per una costante reale e costituiscono una
famiglia di infinite curve ottenibili per traslazione
secondo l’asse y.
19
Def
L’insieme di tutte le primitive di una funzione y = f(x) si
chiama
INTEGRALE INDEFINITO di f(x),
si indica col simbolo:
∫ f ( x)dx
e si legge “Integrale indefinito di f(x) in dx”
20
Allora, riprendendo gli esempi precedenti
(
D (x
)
∫ f ( x)dx = {Pr imitive( f ( x ))}
2
{
}
2
=
Pr
(
2
)
=
+c
xdx
imitive
x
x
∫
∫ cos xdx = {Pr imitive(cos x)} = sin x + c
D (sin x + c ) = cos x
1
1
∫ x dx = Pr imitive x = ln x + c
1
D (ln x + c ) =
x
1
∫ cos 2 x dx =Pr imitive cos 2 x = tgx + c
D (tgx + c ) =
1
D ∫ f ( x )dx = f ( x )
2
)
+ c = 2x
1
cos 2 x
21
Teor. di Torricelli- Barrow (funzione Integrale)
Sia y = f(x) funz. continua nell’intervallo [a, b],
consideriamo un punto x variabile ∈(a, b)
x
∫ f (t )dt
Al variare di x l’integrale
a
assume valori variabili, cioè è una funzione di x che
indicheremo con F(x) e chiameremo funzione integrale
y
f(x)
x
F ( x ) = ∫ f (t )dt
C
D
a
A
x
a
B
b
x
22
In particolare
Se x = a
a
b
F ( a ) = ∫ f (t )dt = 0
se x = b
a
F (b) = ∫ f (t )dt
a
Avremo allora il seguente
Teor. di Torricelli- Barrow
Se y = f(x) è continua in [a, b] allora la funzione integrale
x
F (x) =
∫
f ( t ) dt
a
è derivabile e risulta: F’(x) = f(x);
cioè F(x) è una primitiva di f(x).
23
Dim
Consideriamo l’intervallino [x, x+h]:
avremo
x
y
F ( x ) = ∫ f (t )dt
a
C
D
F ( x + h) =
x+h
∫ f (t )dt
a
A
B
a
x
x+h
b
x
L’incremento di F(x) (area del rettangoloide di base x, x+h) è:
∆F = F (x + h) − F (x) =
x+h
∫
a
x
f ( t ) dt −
∫
f ( t ) dt
a
24
semplificando
∆F =
x+h
x
x
x+h
x
x+h
a
a
a
x
a
x
∫ f (t )dt − ∫ f (t )dt = ∫ f (t )dt + ∫ f (t )dt − ∫ f (t )dt = ∫ f (t )dt
e, per il teorema della media:
∆F =
x+h
∫
f ( t ) dt = f ( c ) h
x
da cui, avremo il rapporto incrementale
∆F F ( x + h) − F ( x)
=
= f (c)
h
h
e, passando al limite per h 0,
F ' ( x ) = lim
h→ 0
F ( x + h) − F ( x)
∆F
= lim
= lim f ( c ) = f ( x )
h
h
h→0
h→ 0
Cioè la derivata di F(x) = f(x)
F ' ( x) = f ( x)
25
Calcolo dell’Integrale Definito
Formula di Newton-Leibniz
Finalmente possiamo calcolare l’integrale definito
b
∫ f (t )dt = area trapezoide
a
Considerando la funzione integrale avremo:
a
x
∫
f ( t ) dt = G ( x ) + c
a
Da cui c = − G(a)
e per x = a
f ( t ) dt = G ( a ) + c = 0
a
x
∫
∫
f ( t ) dt = G ( x ) + c = G ( x ) − G ( a )
a
b
e per x = b
∫ f (t )dt = G(b) − G(a) = [G( x)]a
b
a
26
Teorema fondamentale del calcolo integrale
L’integrale definito di una funzione continua y=f(x),
calcolato nell’intervallo [a, b], è uguale alla differenza
tra i valori che una qualunque primitiva di f(x) assume
agli estremi superiore e inferiore dell’intervallo
d’integrazione.
b
∫ f (t)dt = G(b) − G(a) = [G(x)]
b
a
a
27