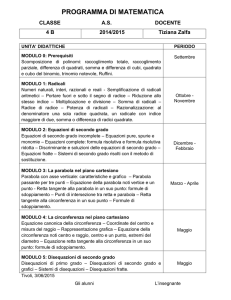
Anno scolastico 2015/16
MATEMATICA CLASSE 3 B ELE
Insegnante
F. Avalle
PROGRAMMA PER IL RECUPERO ESTIVO
Svolgere un adeguato numero di esercizi per ogni argomento, scegliendoli dal testo, e tenendo presenti, come riferimento, le verifiche svolte in
classe durante l’anno, reperibili nel registro elettronico e nella classe virtuale: http://www.itsos-mariecurie.it/corsi/course/view.php?id=863;
le risorse digitali utilizzate quest’anno, sempre nella classe virtuale, e l’anno scorso (soprattutto per il ripasso di algebra, retta e parabola):
http://www.itsos-mariecurie.it/corsi/course/view.php?id=601&sesskey=voDeBBtpzJ&switchrole=5
e gli esercizi svolti e corretti in classe.
Ripassare gli argomenti come li abbiamo affrontati in classe, senza imparare dimostrazioni e formule nuove. I riferimenti al libro di testo che
compaiono nella tabella sottostante sono indicativi: utilizzare soprattutto gli appunti e le risorse digitali della classe virtuale.
Per domande, consigli, chiarimenti: [email protected] oppure il forum nella clase virtuale
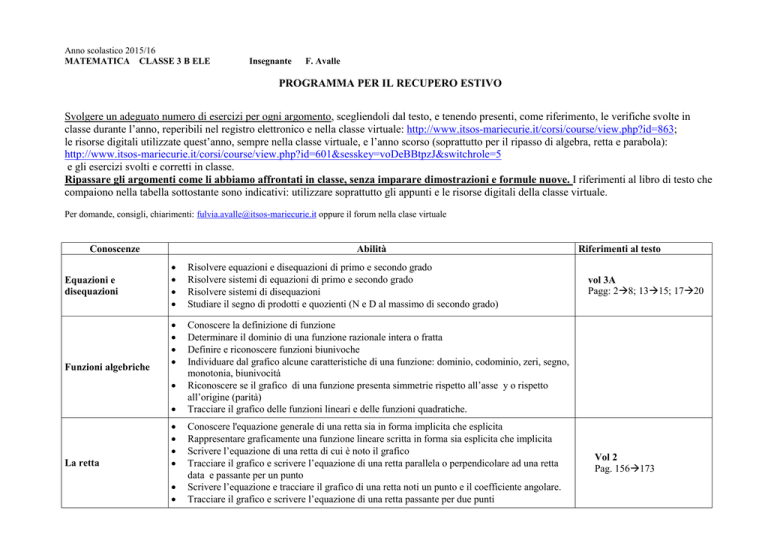
Conoscenze
Equazioni e
disequazioni
Funzioni algebriche
Abilità
Risolvere equazioni e disequazioni di primo e secondo grado
Risolvere sistemi di equazioni di primo e secondo grado
Risolvere sistemi di disequazioni
Studiare il segno di prodotti e quozienti (N e D al massimo di secondo grado)
Conoscere la definizione di funzione
Determinare il dominio di una funzione razionale intera o fratta
Definire e riconoscere funzioni biunivoche
Individuare dal grafico alcune caratteristiche di una funzione: dominio, codominio, zeri, segno,
monotonia, biunivocità
Riconoscere se il grafico di una funzione presenta simmetrie rispetto all’asse y o rispetto
all’origine (parità)
Tracciare il grafico delle funzioni lineari e delle funzioni quadratiche.
La retta
Conoscere l'equazione generale di una retta sia in forma implicita che esplicita
Rappresentare graficamente una funzione lineare scritta in forma sia esplicita che implicita
Scrivere l’equazione di una retta di cui è noto il grafico
Tracciare il grafico e scrivere l’equazione di una retta parallela o perpendicolare ad una retta
data e passante per un punto
Scrivere l’equazione e tracciare il grafico di una retta noti un punto e il coefficiente angolare.
Tracciare il grafico e scrivere l’equazione di una retta passante per due punti
Riferimenti al testo
vol 3A
Pagg: 28; 1315; 1720
Vol 2
Pag. 156173
La parabola
La circonferenza
La funzione
esponenziale
La funzione
logaritmica
Equazioni
esponenziali e
logaritmiche
Goniometria
Riconoscere l’equazione di una parabola con asse verticale
Tracciare il grafico di una parabola, con asse verticale, di cui è data l’equazione
Conoscere la relazione tra il grafico di una parabola e i coefficienti della sua equazione
Scrivere l’equazione di una parabola, assegnate opportune condizioni (anche attraverso il
grafico)
Determinare algebricamente se una retta è tangente, secante o esterna ad una parabola
Definire la circonferenza come luogo geometrico
Riconoscere l’equazione di una circonferenza
Determinare l'equazione di una circonferenza dati raggio e centro
Determinare raggio e centro di una circonferenza data l'equazione
Conoscere le relazioni tra il grafico di una circonferenza e i coefficienti della sua equazione
Determinare le coordinate dei punti di intersezione tra retta e circonferenza
Conoscere la definizione di potenza, con esponente naturale, intero, razionale, reale
Conoscere e saper applicare le proprietà delle potenze ad esponente reale e la formula per il
cambiamento di base
Conoscere le caratteristiche della funzione esponenziale, con base maggiore o minore di uno, e
saperne trcciare il grafico
Conoscere la definizione di logaritmo
Conoscere e saper applicare le proprietà dei logaritmi e la formula del cambiamento di base
Utilizzare la calcolatrice per determinare i valori approssimati di potenze e logaritmi
Conoscere le caratteristiche della funzione logaritmica con base maggiore o minore di 1, e
saperne tracciare il grafico
Determinare il dominio di una funzione logaritmica del tipo 𝑦 = log𝑎 𝑓(𝑥) in casi semplici.
Risolvere semplici equazioni esponenziali e logaritmiche: equazioni elementari, riconducibili
ad elementari con pochi passaggi, riconducibili ad equazioni di secondo grado con sostituzione,
equazioni del tipo 𝑦 = 𝑘 ∙ 𝑎ℎ𝑥 , nell’incognita x oppure y (anche con la calcolatrice e
utilizzando il cambio di base).
Esprimere la misura di un angolo in gradi e radianti. Estendere il concetto di angolo e la sua
misura agli angoli orientati anche maggiori di un giro
Saper convertire l'ampiezza di un angolo da gradi in radianti e viceversa
Conoscere la definizione di seno, coseno , tangente di un angolo acuto come rapporti tra i lati
di un triangolo rettangolo.
Conosce la definizine di seno, coseno e tangente di un angoloqualsiasi utilizzando la
circonferenza goniometrica.
Conoscere le relazioni goniometriche fondamentali tra seno, coseno e tangente di un angolo
Ricavare il valore di seno, coseno, tangente di un angolo mediante la calcolatrice tascabile e,
viceversa, determinare la misura di un angolo conoscendo il valore dei rapporti goniometrici.
Vol 2
Pag. 257 261
vol 3A
pag. 271274; 276
(l’esempio)
vol 3A
pag. 630636
vol 3A
pag. 671677;
vol 3A
pag. 637640
pag. 678; 679; 681.
vol 3A
pag. 386400;
437, 438
516522; 526
Le funzioni circolari
Trigonometria
Conoscere le caratteristiche delle funzioni y= sin(x), y = cos(x), y = tan(x) e tracciarne il
grafico.
vol 3A
pag. 404410
Risolvere triangoli rettangoli isosceli e triangoli equilateri usando solo il teorema di Pitagora
Risolvere i triangoli rettangoli.
vol 3A
pag. 472475
Esprimere un numero complesso in forma algebrica, trigonometrica, esponenziale. Passare da
una forma all’altra.
Rappresentare un numero complesso nel piano di Gauss. Determinare modulo e argomento di
un numero complesso.
Svolgere addizioni, sottrazioni, moltiplicazioni e divisioni tra numeri complessi, utilizzando la
forma più adeguata.
Risolvere semplici equazioni di secondo grado nel campo complesso.
Passare dalle coordinate cartesiane di un punto nel piano alle sue coordinate polari e viceversa.
vol 3A
pag. 584594; 598
Numeri complessi e
coordinate polari
Ricavare e conoscere il valore di seno, coseno, tangente degli angoli di 0°, 30°, 45°, 60°, 90° e
di tutti quelli ad essi associati.
Conoscere le formue di addizione e sottrazione e riconoscere la non linearità delle funzioni
goniometriche.
Risolvere equazioni goniometriche elementari e equazioni riconducibili ad equazioni di
secondo grado.
NB per gli alunni con DSA: nello svolgimento di esercizi, problemi e prove di verifica è sempre consentito l’uso di: calcolatrice scientifica, PC
portatile, tablet o netbook, CAS – Computer Algebra System - (in particolare il CAS del software Geogebra), software grafico (Geogebra, app
grafiche, calcolatrici grafiche…), foglio di calcolo.
Affinché però il loro utilizzo durante le prove sia proficuo occorre che gli alunni siano abituati ad usarlo e ne conoscano a sufficienza tutte le
possibilità, cioè devono imparare ad usarlo!