Dicembre 2016 -VI settimana
L. Seta
18 dicembre 2016
1
Integrazione
1.1
L’integrale indefinito
L’integrale indefinito e l’antiderivazione (libro di testo par 6.1).
• Primitiva di una funzione f (x). Ovvero F (x) è una primitiva di f (x) se F 0 (x) = f (x).
• Tutte le primitive di una stessa funzione differiscono per una costante arbitraria. Ovvero
se F (x) è una primitiva di f (x) allora tutte le altre primitive si possono scrivere come
F (x) + C, con C una costante.
• Integrale indefinito è la famiglia di tutte le primitive di una funzione data f (x), e si indica
con il simbolo:
Z
f (x) dx.
• Valgono le seguenti
Z
d
f (x) dx = f (x);
·
dx
Z
·
F 0 (x) dx = F (x) + C.
• Funzione integranda e la funzione f (x), ovvero la funzione di cui si cerca la primitiva.
• Variabile d’integrazione e la variabile che appare nel differenziale dx.
• Alcuni integrali elementari.
• Linearità. L’integrale definito gode della proprietà seguente, detta di linearità:
Z
Z
(af (x) + bg(x)) dx = a
1
Z
f (x) dx + b
g(x) dx.
1.2
Integrale definito
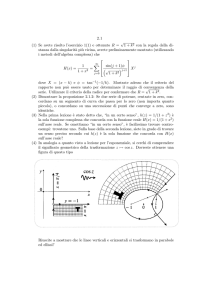
L’integrale definito ha a che fare con il calcolo dell’area determinata dal grafico di una funzione
(libro di testo par. 6.2 e 6.3).
Z b
f (x) dx?
• Cosa significa
a
b
Z
· Attenzione all’ordine degli estremi d’integrazione!
Z
f (x) dx = −
a
a
f (x) dx
b
· Attenzione al segno della funzione integranda! Se f (x) < 0 e a < b allora
b
Z
f (x) dx = −AREA
a
t
Z
• La funzione integrale F (t) =
f (x) dx.
a
• La variazione della funzione integrale:
Z
• Integrale definito e primitiva:
d
F (t) = f (t).
dt
b
f (x) dx = F (b) − F (a).
a
• Proprietà dell’integrale definito:
Z a
f (x) dx = 0;
· Area nulla
a
b
Z
· Ordine degli estremi d’integrazione
Z
f (x) dx = −
a
b
Z
· Costante moltiplicativa
· Composizione di aree
f (x) dx;
b
Z
b
f (x) dx;
αf (x) dx = α
a
a
Z
a
b
Z
c
f (x) dx =
a
Z
f (x) dx +
a
b
f (x) dx.
c
• Integrabilità delle funzioni continue
• Integrale di Riemann
1.3
Applicazioni economiche
Confrontare il libro di testo paragrafo 6.4. In particolare il par. 6.4.4 Surplus del consumatore
e del produttore.
1.4
Principali tecniche di integrazione
• Decomposizione in somma:
Z
Z
Z
f (x) + g(x) dx = f (x) dx + g(x) dx.
Si usa in particolare, ma non solo, per i seguenti integrali (una volta applicate le formule
che fanno passare dal prodotto alla somma, vedi sotto):
2
·
R
sin(λx) sin(µy) dx con λ e µ costanti;
·
R
cos(λx) cos(µy) dx con λ e µ costanti;
·
R
sin(λx) cos(µy) dx con λ e µ costanti;
·
R
sinn (λx) cosm (µy) dx con λ e µ costanti ed n ed m non entrambi pari;
• Integrazione per sostituzione. Alcuni integrali immediati:
Z
1
f (x)α+1 + C con α 6= −1;
·
f (x)α f 0 (x) dx =
α+1
Z 0
f (x)
·
dx = log |f (x)| + C;
f (x)
Z
·
ef (x) f 0 (x) dx = ef (x) + C;
Z
·
cos f (x)f 0 (x) dx = sin f (x) + C;
Z
·
sin f (x)f 0 (x) dx = − cos f (x) + C;
Z
f 0 (x)
·
dx = arctan f (x) + C;
1 + f (x)2
2
La prossima settimana
La settimana sarà dedicata a completare lo studio dell’integrazione e all’introduzione delle funzioni
di più variabili (in parentesi i paragrafi corrispondenti sul libro di testo).
• Integrazione per parti (par. 6.5);
• Integrazione funzione razionali;
• Funzione di due variabili (8.1; 8.2; 8.3);
• Problemi di ottimizzazione libera (10.1; 10.2; 10.3);
• Ottimizzazione vincolata (11.1; 11.2).
3
Suggerimenti, consigli
• Studiare gli esempi economici del libro. In particolare, paragrafo 6.4.4 ed esempio 6.12.
• Ripetere le principali formule trigonometriche
· Identità fondamentali
sin2 x + cos2 x = 1
1 + tan2 x = sec2 x
1 + cot2 x = csc2 x
3
· Somma e differenza di angoli
sin(x + y) = sin x cos y + cos x sin y
sin(x − y) = sin x cos y − cos x sin y
cos(x + y) = cos x cos y − sin x sin y
cos(x − y) = cos x cos y + sin x sin y
tan x + tan y
tan(x + y) =
1 − tan x tan y
tan x − tan y
tan(x − y) =
1 + tan x tan y
· Duplicazione
sin(2x) = 2 sin x cos x
cos(2x) = cos2 x − sin2 x
= 2 cos2 x − 1
= 1 − 2 sin2 x
2 tan x
tan(2x) =
1 − tan2 x
· Dimezzamento
r
x
1 − cos x
sin = ±
2
2
r
x
1 + cos x
cos = ±
2
2
x
1 − cos x
tan =
2
sin x
sin x
=
1 + cos x
· Riduzione delle potenze
1 − cos 2x
2
1 + cos 2x
2
cos x =
2
1 − cos 2x
2
tan x =
1 + cos 2x
sin2 x =
· Da prodotto a somma
4
sin x sin y =
cos x cos y =
sin x cos y =
tan x tan y =
tan x cot y =
1
cos(x − y) − cos(x + y)
2
1
cos(x − y) + cos(x + y)
2
1
sin(x + y) + sin(x − y)
2
tan x + tan y
cot x + cot y
tan x + cot y
cot x + tan y
· Da somma a prodotto
sin x + sin y = 2 sin
x + y sin x − sin y = 2 cos
cos x + cos y
cos x − cos y
tan x + tan y
tan x − tan y
2 x +
y
cos
x − y 2 x −
y
sin
2
2 x + y x −
y
= 2 cos
cos
x2− y x2 + y sin
= −2 sin
2
2
sin(x + y)
=
cos x cos y
sin(x − y)
=
cos x cos y
• Può essere utile conoscere le funzioni iperboliche (combinazioni di funzioni esponenziali)
così definite:
cosh x =
ex + e−x
,
2
tanh x =
sinh x =
ex − e−x
2
sinh x
ex − e−x
= x
cosh x
e + e−x
• Ecco alcune formule utili:
· cosh2 x − sinh2 x = 1;
· sinh(x ± y) = sinh x cosh y ± cosh x sinh y;
· cosh(x ± y) = cosh x cosh y ± sinh x sinh y;
tanh x ± tanh y
· tanh(x ± y) =
;
1 ± tanh x tanh y
· sinh 2x = 2 sinh x cosh x;
· cosh 2x = cosh2 x + sinh2 x;
cosh 2x + 1
· cosh2 x =
;
2
5
· sinh2 x =
cosh 2x − 1
.
2
• Funzioni iperboliche inverse Si introducono le funzione inverse delle funzioni iperboliche.
La funzione inversa del sinh(x) si indica in vari modi: sinh−1 (x) oppure arcsinh (x), e ancora
settsinh (x), detta settore seno iperbolico. In modo analogo per le altre funzioni iperboliche.
Inoltre valgono le seguenti:
√
· sinh−1 (x) = log x + x2 + 1 ;
√
· cosh−1 (x) = log x + x2 − 1 ;
1
1+x
−1
· tanh (x) = log
;
2
1−x
• Le derivate di queste funzioni sono date da:
· Dx (sinh x) = cosh x
· Dx (cosh x) = sinh x
1
· Dx (tanh x) =
cosh2 x
1
· Dx (sinh−1 x) = √
x2 + 1
1
· Dx (cosh−1 x) = √
se cosh−1 x > 0
2
x −1
−1
· Dx (cosh−1 x) = √
se cosh−1 x < 0
2
x −1
1
· Dx (tanh−1 x) =
1 − x2
• L’uso di queste funzioni risulta utile per la soluzione di alcuni integrali irrazionali:
Z
√
dx
−1
2
√
·
= sinh x + C = log x + x + 1 + C
x2 + 1
Z
√
dx
√
·
= cosh−1 x + C = log x + x2 − 1 + C
x2 − 1
√
√
√
Z √
−1
2 + 1 + x x2 + 1
2+1
log
x
+
x
sinh
x
+
x
x
·
x2 + 1 dx =
+C =
+C
2
2
√
√
√
Z √
−1
2 − 1 + x x2 − 1
2−1
−
log
x
+
x
−
cosh
x
+
x
x
·
x2 − 1 dx =
+C =
+C
2
2
Z
1 + x
dx
1
−1
+C
·
= tanh x + C = log 1 − x2
2
1 − x
6
4
Esercitiamoci
Esercizio 1. Risolviamo i seguenti integrali indefiniti immediati (semplice sostituzione della variabile d’integrazione):
√
Z
Z
1
dx
a)
(2 + 5x)3
Z
1
c)
dx
x log(x)
Z
x3
e)
dx
1 + x8
b)
1 + 2x dx
Z
log(x)
dx
x
Z
dx
√
f)
x (1 + x)
d)
Esercizio 2. Risolviamo i seguenti esercizi utilizzando la decomposizione in somme:
e2x
√ x
dx
e −1
Z √ 2
x − a2
d)
dx
x
Z 3
x +x+1
f)
dx
x2 + 1
Z
Z
dx
√
√
a)
x+1+ x−1
Z
1
c)
dx
1 + e2x
Z
e)
4x4 + 3x2 + 5x dx
b)
Esercizio 3. Risolviamo i seguenti integrali indefiniti utilizzando la trasformazione trigonometriche:
Z
Z
a)
sin(2x) cos(x) dx
b)
sin2 (x) cos3 (x) dx
Z
Z
1
dx
c)
cos(x) sin(3x) dx
d)
tan2 (x)
Esercizio 4. Provare a risolvere i seguenti integrali indefiniti utilizzando la sostituzione x = sin(t)
e dx = cos(t) dt:
a)
Z √
Z
1−
x2
dx
b)
√
1
dx
1 − x2
Esercizio 5. Risolviamo i seguenti integrali indefiniti:
Z
a)
Z
1
√
dx
4
2x + 1
b)
Z
cos(ax) dx
c)
Z
e)
Z
d)
2
3xex dx
1
dx
1 + cos(x + a)
Z
1
dx
2
3x + 2
f)
7
sin(3x) sin(2x) dx
Esercizio 6. Data la funzione definita nell’intervallo [0, 1] da:
(
0, se x ∈ (0, 1]
f (x) =
5, se x = 0
Verifica che f (x) la funzione ha integrale nullo in [0, 1].
Esercizio 7. Calcoliamo l’integrale:
Z
2π
sin2 x dx.
0
Esercizio 8. Considerato il risultato dell’esercizio precedente, e ricordando il significato geometrico dell’integrale definito verifichiamo che:
Z
2π
Z
2
sin x dx =
0
0
8
2π
cos2 x dx = π.