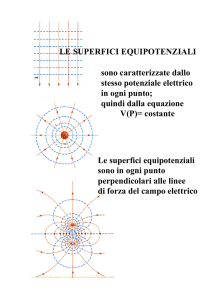
Due cariche puntiformi q1=50 µC e q2 =100 µC
sono separate da una distanza c=1.0 m; Quale è il campo
elettrico nel punto intermedio. Quale sarebbe la forza
esercitata su una carica q3=20 µC collocata in questo punto?
E1 =
E2 =
1
q1
4πε 0 (c/2) 2
1
q2
4πε 0 (c/2) 2
= 8.988 ⋅10
50 ⋅10 -6
9
= - 8.988 ⋅10
(0.5) 2
9
= 1.80 ⋅ 10 6 NC -1
100 ⋅10 -6
(0.5) 2
= −3.60 ⋅ 10 6 NC -1
6
E = E a + Eb = −1.80 ⋅ 10 NC
F = Eq3 = −36.0 N
-1
Forze in un sistema di cariche
sovrapposizione degli effetti
q1
+
q2
F2
F3
+
q3
+
q
=
+
q
F4
F1
q4
F
F = F1 + F 2 + F 3 + F 4
F=
1
q q1
4πε 0 r1
F=
2
u r1 +
1
q q2
4πε 0 r2
2
u r 2 + ... +
i
q qN
4πε 0 rN
qi
q
4π ε 0
1
ri
2
u
ri
2
u rN
Calcolare la forza sulla carica Qo=100 µC posta
sull’asse z a 3 m dall’origine se quattro cariche Q= 20
µC sono disposte simmetricamente sugli assi x ed y a 4
m dall’origine
z
P
Qo
Px2
Py2
Py1
x Px1
y
Per simmetria, le componenti
delle singole forze non dirette
lungo z si elidono
Ftot = Ftot u z =
Qo Q
πε 0 ry1
2
u z = (0 0 1.726 ) N
Il numero di cariche coinvolte nei fenomeni di
elettromagnetismo è così elevato che ha senso
studiare i campi originati da distribuzioni continue
La forza F che agisce sulla carica q0 (posta in r), a causa dell’elemento di carica
infinitesimo dq = ρ(r’) dV’, posto in r’, vale:
F (r ) = q0 ρ (r ' )dV '
V
r − r'
4πε 0 r − r '
ρ è una densità volumica di carica [C/m3 ]
3
Densità di carica ‘volumica’
Carica totale distribuita nel volume V :
Volume V
Carica Q
dq
ρ=
dV
Q=
V
dV
ρ dV
(unità di misura nel SI: C m-3)
dq
Densità superficiale di carica
Superficie S
Carica Q
(unità di misura nel SI: C m-2)
dq
σ=
dS
dS
Carica totale distribuita sulla superficie
S:
Q=
S
σ dS
dq
Densità lineare di carica
(unità di misura nel SI: C m-1)
linea l
dq
λ=
dl
Carica totale distribuita sulla
lunghezza l:
Q=
l
λ dl
Carica Q
dq
dl
L’integrale:
F (r ) = q0 ρ (r − r ' )dV '
V
r − r'
4πε 0 r − r '
3
è di difficoltà enorme tranne in rari casi!!!
Campo Elettrico
F
E=
q0
[N C ]
−1
Unità di misura nel SI: newton/coulomb (NC-1 = Vm-1)
Esempi di valori di campi elettrostatici
- Campo creato dal protone dell'atomo di idrogeno alla distanza di
un raggio di 5.29*10-11 m
6 1011 N C-1
- In una membrana cellulare
7 106 N C-1
- In un acceleratore di particelle
2 105 N C-1
- In un tubo televisivo
2 104 N C-1
- Campo elettrico terrestre
102 N C-1
- Nei metalli
0
Campo ELETTRICO generato in P dalla carica puntiforme q1
.P
r1
q1
1
q1
ˆ
E=
2 r1
4 πε 0 r1
Esercizio (lug-2003) Si calcoli il campo elettrico nel punto
(0,0,0) prodotto da 4 cariche uguali di valore q=10mC
collocate nei punti P1(1,1,0), P2(-1,1,0), P3(-1,-1,0) e P4(1,1,0). (Le misure sono in cm).
Linee di campo
E è tangente in ogni punto alla linea di forza (di campo)
E
E
E
Conduttori, isolanti, semiconduttori
Conduttori : sostanze nelle quali alcune o tutte le cariche
elettriche possono muoversi liberamente sotto l'azione di forze
elettriche (elettroni di conduzione nei metalli, ioni nelle
soluzioni acquose).
Isolanti (dielettrici): gli elettroni sono vincolati agli atomi (es.:
vetro, ebanite).
Semiconduttori: classe di materiali intermedia tra i conduttori
e gli isolanti per le loro proprietà di condurre elettricità (es. :
silicio, germanio).
Nei conduttori:
E int = 0
Nei conduttori:
INDUZIONE ELETTRICA NEI CONDUTTORI:
ELETTROSCOPIO
Elettroscopio
ELETTROMETRO
Dipolo Elettrico: simmetria cilindrica
il campo non dipende da φ
P
z
d
2
d
−
2
(+)
ϑ
r(+ )
r
r(− )
x
(−)
E( r , ϑ , φ ) = E ( + ) ( r , ϑ ) + E ( − ) ( r , ϑ )
E(+) =
q
r( + )
4πε 0 r(2+ )
r( + )
E( r , ϑ ) =
E (−) =
q
r( + )
4πε 0 r(2+ )
r( + )
−
q
(−q)
r( − )
4πε 0 r(2−) r( −)
r( −)
4πε 0 r(2+ ) r( − )
u
P
z
d
2
d
−
2
(+)
ϑ
r
u
θ
r(+ )
r
r(− )
x
(−)
r( + ) = r( − ) − d u z
in coordinate sferiche:
u z = cos ϑ u r − sin ϑ u ϑ
E( r , ϑ ) =
q
4πε 0 r(3+ )
(r
( −)
)
− duz −
q
r(3− ) − r(3+ )
4πε 0
r(3− ) r(3+ )
r( − ) −
essendo : r( ± ) = r
r(3−)
− r(3+ )
q
4πε 0 r(3− )
d
r(3+ )
r( − ) =
uz
d
cos ϑ
2
d
3
2 d
≈ r + 3r
cos ϑ − r − 3r
cos ϑ = 3r 2 d cos ϑ
2
2
3
2
E( r , ϑ ) ≈
q
3r 2 d cos ϑ
4πε 0
r(3− ) r(3+ )
r( −) −
d
r(3+ )
uz
essendo inoltre r( ± ) ≈ r e r( −) ≈ r u r
E( r , ϑ ) ≈
q
4πε 0
2
3r d cos ϑ
r
6
ru r −
d
r
3
(cosϑ u r − sin ϑ uϑ )
in definitva :
E( r , ϑ ) ≈
q
4πε 0 r
(
)
d
ϑ
u
+
d
ϑ
u
2
cos
sin
r
ϑ
3
Momento di dipolo elettrico p
p = qd
E( r , ϑ , φ ) ≈
p
4πε 0 r
3
(2 cosϑ u r + sin ϑ uϑ )
Si noti come E dipenda solo da p: se q raddoppia
e d si dimezza (o viceversa) E non cambia!!!
applet_italia\Linee_di_campo.ht
m
Molecola d’acqua
Dipolo ancorato in un campo
elettrico uniforme
Il momento torcente τ che agisce sul dipolo
ancorato al centro:
1
τ = d / 2× F = p× E
2
τ = d / 2 F sin θ =
qdE sin θ / 2 = pE sin θ / 2
τ fa ruotare il dipolo in senso orario fino a
farlo allineare con E (θ=0) !!!
Se il campo esterno varia nel tempo
E tot = E + E dipolo
-
+
x
Ex + ∂ x Exd
−Q
-
Ex
∆x
+
Q
x
Fx = ( E x ( + ) − E x ( − ) )Q = ∂ x E x Q ∆x = p x ∂ x E x
lim E x ( x + h) − E x ( x)
∂ x Ex =
h →0
h
La forza esercitata su un dipolo elementare p dal campo elettrico E,
diretto lungo x, è data dalla formula:
Fx = p ⋅ ∇E x = p x ∂ x E x + p y ∂ y E x + p z ∂ z E x
∇f = ∂ x f i x + ∂ y f i y + ∂ z f i z
ANALOGAMENTE SI PROCEDE PER LE ALTRE COMPONENTI di F
Fx = p ⋅ ∇E x
F y = p ⋅ ∇E y
Fz = p ⋅ ∇E z
Fx = 0
il campo è costante (∇E x = 0)
p è nullo
se
p è ortogonale a∇E x
Nel caso di dipoli indotti
• p è parallelo al campo
Il fenomeno dell’induzione
elettrostatica nei dielettrici
Molecole polari e non
In presenza di un campo elettrico..
Anche in molecole non polari, in presenza di un
campo esterno, ciascun atomo viene polarizzato.
Polarizzazione in uno strato dielettrico
E
-
+
E pol
-
E
+
E tot = E + E pol
Campo elettrico di un anello carico
sull’asse di simmetria
La carica dq genera in P dE
dq
λds
λds
=
=
4πε 0 r 2 4πε 0 r 2 4πε 0 z 2 + R 2
dE =
(
Tenuto conto che
λ=
dq = λds
Q
2πR
s
E = dE cos ϑ =
0
E=
(
Qz
4πε 0 z 2 + R 2
cos ϑ =
)
3
2
uz
(
z
=
r
(z
λz
2
4πε 0 z + R
z
2
+ R2
s
2
)
3
2 0
)
)
ds =
zλ (2πR )
(
2
4πε 0 z + R
Q
Per
z >> R
E→
Per
z=0
E→0
4πε 0 z 2
2
)
3
2
Campo elettrico di un disco carico sull’asse di simmetria
All’interno del disco l’areola dA contiene dq = σdA
σ=
dA = 2πrdr
dE =
dq z
(
4πε 0 z 2 + r 2
E=
r=R
dE =
r =0
)
3
=
2
zσ
4ε 0
R
0
zσ 2πrdr
(
4πε 0 z 2 + r 2
(
2
2
+ r2
d z +r
(z
2
)
3
πR 2
)
3
2
) = zσ
2
E=
quando
Q
4ε 0
zσ
=
4ε 0
(z
(z
(− 2)
2
+ r2
2rdr
2
+ r2
)
R
)
1
=
2
0
3
2
(
(
)
zσ 2 1
1
−
4ε 0 z
z2 + R2
z
σ
uz
1−
2ε 0
z2 + R2
σ
z = 0 E =
2ε 0
)
zσ d z 2 + r 2
=
3
4ε 0 2
z + r2 2
z
σ
E( z R ) =
1−
2ε 0
z2 + R2
σ
≈
2ε 0
1 R2
−z
z 1+
2
2 z
z2 + R2
uz
σ
uz =
2ε 0
z2 + R2 − z
z2 + R2
Q
1 1 R2
uz =
u
≈
2
2 z
2
πR 2ε 0 2 z
4πε 0 z
Q
Quindi a grande distanze, sull’asse di simmetria
E( z R ) =
uz =
Q
4πε 0 z
2
uz
E=
σ
z
1−
2ε 0
z2 + R2
Piano indefinito
quando R → ∞
σ
E→
2ε 0
Moto di una particella carica in E
y
Fe
v0
x
Lungo l’asse x
Lungo l’asse y
Forze agenti:
Fx=0
Forze agenti:
Fy=eE (e<0)
Accelerazioni:
ax=Fx/me=0
Accelerazioni:
ay=Fy/me=eE/me≠0
Velocità:
vx=v0x+axt=v0=cost
Velocità:
vy=v0y+ayt= eEt/me
Spostamento:
x=vx0t
Spostamento:
y=vy0t+ayt2/2= eEt2/(2me)
moto uniforme
moto uniformemente accelerato
Equazione del moto:
y=
eE
2
2 me v 0
x
2
(parabola)
In assenza di campo elettrico
Moto di caduta libera
FA
4 3
πr ρ o g
3
attrito= 6πηrv
Fp=forza peso=
S
FA=forza di
S=spinta di Archimede=
Fp
(Stokes)
4 3
πr ρ a g
3
Equazione del moto
Fp=FA+S
4 3
πr g (ρ o − ρ a ) = 6πηrv
3
Fe
Fp
E
In presenza di campo elettrico
La particella rimane ferma sotto
l’equilibrio tra forza peso e forza
elettrostatica Fe
Fe=forza elettrostatica=eE
Equazione del moto
Fp=Fe
Esperienza di Millikan
(1909-1917)
Esperienza di Millikan II
4 3
P = πa ρg Forza peso ( ρ = 800 kg m −3 )
3
4 3
P' = − πa ρ ' g Spinta di Archimede ( ρ ' = 1.29 kg m −3 )
3
F1 = −6πηav Attrito (η = 1.8 ⋅10
−5
Nsm −2 )
F2 = −qE Forza di Coulomb
d
m v = P + P'+ F1 + F2
dt
4 3
6πηa
πa (ρ − ρ ')g − qE
−
t
3
v(t ) =
1− e m
6πηa
vlim
4 3
πa (ρ − ρ ')g − qE
= 3
6πηa
4 3
πa (ρ − ρ ')g − qE
a= 3
6πηvlim
Quindi, misurata vlim, si è in grado di riconoscere a, il raggio della gocciolina.
Se ora scegliamo E in modo tale che la gocciolina sia in equilibrio (v=0), risulta:
4 3
πa ρg
q= 3
E
I valori di q che si ottengono sono multipli della carica dell’elettrone
Riassunto
•
•
•
•
•
Elettrizzazione
Struttura della materia, protoni ed elettroni
Neutralità della carica
Conservazione della carica
Legge di Coulomb per due cariche puntiformi nel
vuoto
• Confronto fra le forze gravitazionali ed
elettrostatiche
• Generalizzazione al caso di n cariche
• Distribuzioni continue di carica
•
•
•
•
•
•
•
•
Campo Elettrico
Campo generato da una carica puntiforme
Campo generato da un dipolo
Campo di un anello uniformemente caricato
Campo di un dipolo
Campo di un disco
Moto di una particella carica in un campo
Esperimento di Millikan