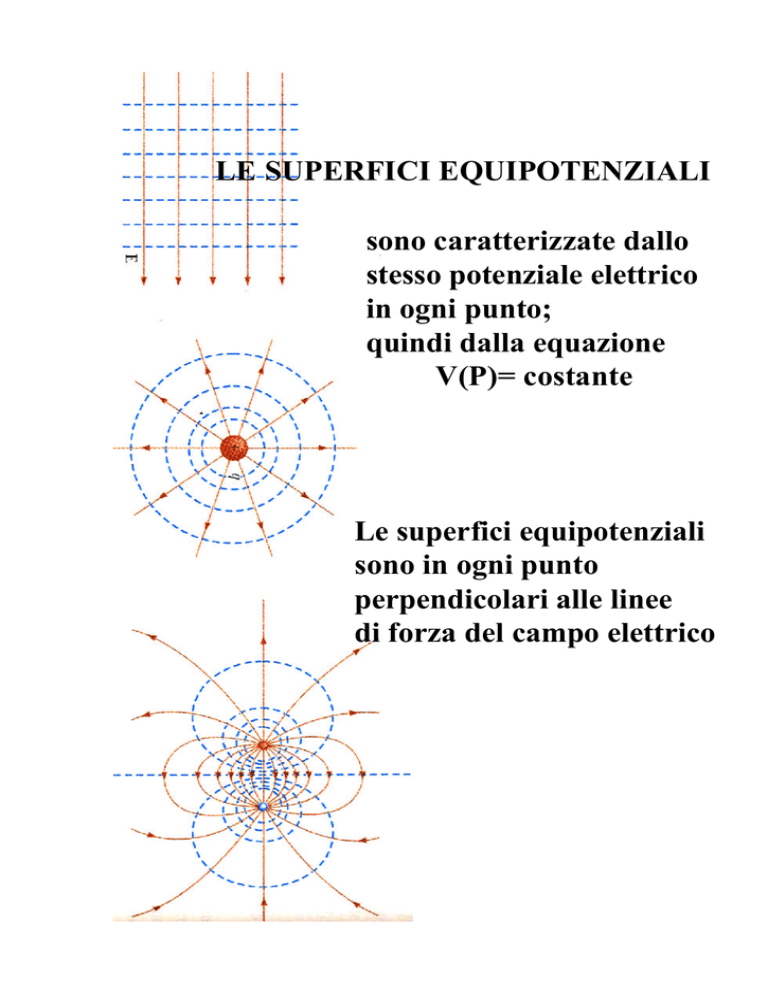
LE SUPERFICI EQUIPOTENZIALI
sono caratterizzate dallo
stesso potenziale elettrico
in ogni punto;
quindi dalla equazione
V(P)= costante
Le superfici equipotenziali
sono in ogni punto
perpendicolari alle linee
di forza del campo elettrico
DIPOLO ELETTRICO
è formato da due cariche puntiformi di segno opposto
+q ,-q separate da una distanza d. Il momento di dip.
elettrico è definito come il vettore di modulo p=qd
con verso -q ---> +q
d
il potenziale in un generico punto di coordinate
(x,y,z) vale:
d
2
d
2
Nell’ipotesi di grande distanza
r = (x2+y2+z2)1/2 >> d
il potenziale diventa
1 1
q r2 − r1
− =
=
r1 r2 4πε o r1 ⋅ r2
q d cos Θ p cos Θ
=
=
2
4πε o r
4πε o r 2
z=r cos θ
1 pz
Φ (P ) =
4πε 0 r 3
q
Φ (P ) =
4πε o
Veniamo adesso al calcolo
del campo elettrico
r
r
E = −∇Φ (P )
INTERAZIONE DI UN DIPOLO
ELETTRICO CON UN CAMPO ELETTRICO
ESTERNO UNIFORME
Supponiamo di mettere un dipolo elettrico
p=qd in un campo elettrico unforme E, ma non
orientiamolo parallelamente al campo elettrico.
La forza netta agente sul dipolo è nulla,
ma si crea un momento:
τ = (q d sinϑ ) E = p E sinϑ
r r r
τ = p× E
E
θ
In conclusione: il dipolo tende ad allinearsi
parallelamente al campo elettrico
La capacità elettrica e i condensatori
Se prendiamo un conduttore isolato su cui si
trova la carica Q si può dimostrare che qualunque
sia la geometria
la carica Q è proporzionale al potenziale V
Q = CV
La costante C è detta capacità elettrica del conduttore.
ESEMPIO: prendiamo una sfera metallica
di raggio R con carica Q:
Q
V=
4πεR
E quindi:
C = 4πεR
La capacità si misura in FARAD [F]=CV-1 nel S.I.
Quando prendiamo due conduttori isolati
su cui abbiamo posto due cariche Q uguali
in modulo ma di segno opposto
abbiamo un CONDENSATORE
e si può dimostrare che qualunque sia la
geometria del sistema
Q = C∆V
Dove ∆ V è la diff. di pot. tra i metalli
e C dipende solo dalla geometria e dal
dielettrico in cui il condensatore è immerso.
Il condensatore a facce piane e parallele
DATI:
area facce S;
carica Q;
densità di carica
σLIB=Q/S
Q σ LIB
E=
=
εS
ε
V1 − V2 = E ⋅ d =
Q
C=
∆V
Senza dielettrico tra le
piastre risulterebbe
σ LIB d Q ⋅ d
=
ε
S ⋅ε
εS ε 0ε r S
C=
=
d
d
ε0S
C0 =
d
La Capacità C di un condensatore risulta
incrementata di un fattore εr rispetto all’assenza di
dielettrico (vuoto tra le piastre)
Energia del campo elettrostatico
Se cerchiamo di caricare un condensatore a facce
piane parallele di capacità C, il lavoro fatto
per portare la carica dq sulle facce vale:
dL = Vdq
Ma V è la diff. di pot. tra le armature
q
V=
C
Per il caricamento totale si fa un lavoro
V0
Q
V0
V0
2
q
1Q
L = ∫ Vdq = ∫ dq =
C
2 C
0
0
1
2
L = ∫ Vdq = ∫ Vd (CV ) = CV0
2
0
0
Dove va a finire il lavoro L del generatore per
caricare il condensatore ?
Nella costruzione del campo elettrico dentro
il condensatore.
Quindi diventa energia del campo elettrostatico.
Vediamo di calcolare questa energia in funzione
di E per un condensatore a facce piane e parallele:
1
L = CV0 2 = W en. campo elettr.
2
εS
ma ricordando : C = ; V0 = Ed
d
1 εS
1 2
2
W = ( )( Ed ) = εE ( Sd )
2 d
2
Introducendo il concetto di densità di energia del
campo elettrostatico:
W
1 2
w=
= εE
( Sd ) 2
Si può dimostrare che il risultato è generalizzabile a
qualsiasi campo elettrostatico.
•Serie e paralleli di condensatori
capacità in serie
capacità in parallelo
1
=
Ceq
∑
C eq =
1
Ci
∑C
i












