Soluzioni prova del 4-9-15

FISICA GENERALE I
Cognome
Corso di Studi
Voto:
Esercizio n. 1
A.A. 2014-2015
4 SETTEMBRE
Nome
Docente
matricola
CFU
8-9
2015
10
12
Ritirato (barrare e firmare) :
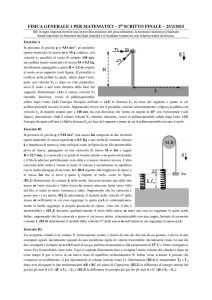
Un corpo di massa m è vincolato a muoversi senza attrito lungo l’asse x ed è inizialmente in
quiete nell’origine. Ad un certo istante, al corpo viene applicata una forza di modulo costante F,
la cui direzione rispetto all’asse x varia secondo la legge α(x)=kx rad, dove x rappresenta la
distanza percorsa dal corpo. Calcolare a): l’espressione dell’energia cinetica in funzione di x e il
valore della velocità massima raggiunta del corpo; b) la distanza percorsa per raggiungere tale
velocità. Eseguire i calcoli per: m=1kg, F=9N, k=2rad/m.
𝑥
a)Dal teorema delle forze vive : ∆𝐾 = ∫0 𝐹𝑐𝑜𝑠𝑘𝑥 𝑑𝑥 , quindi
1
F
α(x)
x
𝐹
m𝑣 2 = 𝑘 𝑠𝑖𝑛𝑘𝑥 .
2
Dall’espressione dell’energia cinetica si ricava la velocità, cioè
2𝐹𝑠𝑖𝑛𝑘𝑥
𝑣(𝑥) = √
𝑚𝑘
𝑚
. La velocità massima dunque si raggiunge per sinkx=1, cioè 𝑣𝑚𝑎𝑥 = 3 𝑠 .
b)Se sinkx=1 allora 𝑘𝑥 = 𝜋/2 e quindi la corrispondente distanza del corpo dall’origine è
𝜋
𝑥 = 4 =0.78m
Esercizio n. 2
Una pallina di massa m è collegata ad un estremo di una molla ideale di costante elastica K e
lunghezza a riposo nulla ed è vincolata ad una guida orizzontale liscia sulla quale può
scorrere. L’altro estremo della molla è fissato sull’asse y, a distanza d dall’origine. Alla
pallina è applicata una forza orizzontale F, in modo che sia in equilibrio. Determinare la
distanza x0 della pallina dall’origine O. Improvvisamente la forza F cessa di agire e la
pallina, muovendosi lungo l’asse x, urta in modo completamente anelastico un’altra pallina
identica posta in O: calcolare la massima distanza raggiunta dal sistema rispetto all’origine.
Eseguire i calcoli per: m= 1kg , K=400N/m, F=100N.
y
d
O
x
F
All’equilibrio si ha 𝐹 − 𝑘∆𝑙𝑠𝑖𝑛𝜗 = 0 dove 𝜗 è l’angolo tra l’asse y e la direzione della molla e ∆𝑙 è
l’allungamento della molla , per cui ∆𝑙𝑠𝑖𝑛𝜗 = 𝑥0 .
𝐹
Quindi 𝑥0 = 𝑘 = 0.25𝑚.
Prima dell’urto con la seconda pallina, si ha la conservazione dell’energia meccanica, cioè:
1
2
𝑚𝑣 2 +
1
2
1
𝑘𝑑 2 = 2 𝑘(𝑥02 + 𝑑 2 ).
𝑘𝑥 2
Quindi, nell’istante dell’urto, la velocità della prima pallina è 𝑣 = √ 𝑚0 = 5
𝑚
𝑠
𝑣
Nell’urto si conserva la quantità di moto e dunque 𝑚𝑣 = 2𝑚𝑣𝑐𝑚 da cui 𝑣𝑐𝑚 = 2.
Subito dopo l’urto, si ha ancora conservazione dell’energia meccanica, cioè:
1
1
1
𝑚𝑣 2
2
2
2𝑚𝑣𝑐𝑚
+ 2 𝑘𝑑 2 = 2 𝑘(𝑑2 + 𝑥𝑚𝑎𝑥
) da cui 𝑥𝑚𝑎𝑥 = √
2
2𝑘
= 0.18 𝑚
Esercizio n. 3
Una sbarra omogenea di lunghezza L e massa M è inclinata di un angolo θ rispetto alla
verticale ed è inizialmente in quiete con l’estremo inferiore ad una quota h rispetto al piano
orizzontale. La sbarra viene lasciata cadere, l’estremo A tocca il suolo rimanendovi
vincolato e la sbarra inizia a ruotare intorno ad A. Calcolare la velocità angolare della sbarra
subito dopo l’urto e nell’istante in cui anche l’estremo B tocca il suolo. Eseguire i calcoli
per: L=0.8m, θ=30°, h=0.6m.
B
h
θ
A
Durante la caduta, si conserva l’energia meccanica:
𝑀𝑔ℎ =
1
2
𝑀𝑣02 da cui 𝑣0 = √2𝑔ℎ
𝐿
Nell’urto si conserva il momento angolare rispetto al polo A: 𝑀𝑣0 2 𝑠𝑖𝑛𝜗 = 𝐼𝜔
da cui 𝜔 =
3
2
𝑣0
𝑠𝑖𝑛𝜃
𝐿
con 𝐼 =
1
3
𝑀𝐿2
= 3.2 rad/s.
Dopo l’urto si conserva l’energia meccanica e quindi
1
2
𝐿
𝐼𝜔2 + 𝑀𝑔 2 𝑐𝑜𝑠𝜗 =
1
2
𝐼𝜔′2
da cui 𝜔′ = √𝜔 2 +
3𝑔𝑐𝑜𝑠𝜗
𝐿
= 6.5 𝑟𝑎𝑑/𝑠
Esercizio n. 4
Una mole di gas ideale è contenuta in un cilindro verticale di sezione S nel quale può scorrere un pistone ideale. Il cilindro
è in contatto con una sorgente a temperatura T e il gas si trova in equilibrio a pressione p0. Ad un certo istante un corpo di
massa M viene appoggiato sul pistone che si abbassa di Δh e il sistema raggiunge un nuovo stato di equilibrio. Calcolare la
variazione di entropia del gas e il calore scambiato con la sorgente. Eseguire i calcoli per: S=10-2m2, p0=105Pa, M=20kg,
Δh=0.2m.
La trasformazione è irreversibil, con la temperatura iniziale e finale che coincidono.
Per il calcolo della variazione di entropia, consideriamo una trasformazione isoterma reversibile, per cui:
∆𝑆𝑔𝑎𝑠 = 𝑛𝑅 𝑙𝑛
Essendo Ti=Tf ,
𝑉𝑓
𝑝𝑖
𝑝0
𝐽
= 𝑛𝑅 𝑙𝑛 = 𝑛𝑅 𝑙𝑛
= −1.5
𝑀𝑔
𝑉𝑖
𝑝𝑓
𝐾
𝑆 + 𝑝0
𝑄𝑔𝑎𝑠 = 𝑊𝑔𝑎𝑠 dove 𝑊𝑔𝑎𝑠 = −𝑊𝑒𝑥𝑡 = −(𝑀𝑔 + 𝑝0 𝑆)∆ℎ
e quindi 𝑄𝑔𝑎𝑠 = −239 𝐽