FISICA GENERALE 1 PER MATEMATICI – 2o SCRITTO FINALE – 25/2/2015
NB:$in$ogni$risposta$fornire$una$breve$illustrazione$del$procedimento,$la$formula$risolutiva$(risultato$
finale$espresso$in$funzione$dei$dati$iniziali)$e$il$risultato$numerico$con$relativa$unità$di$misura.
Esercizio A
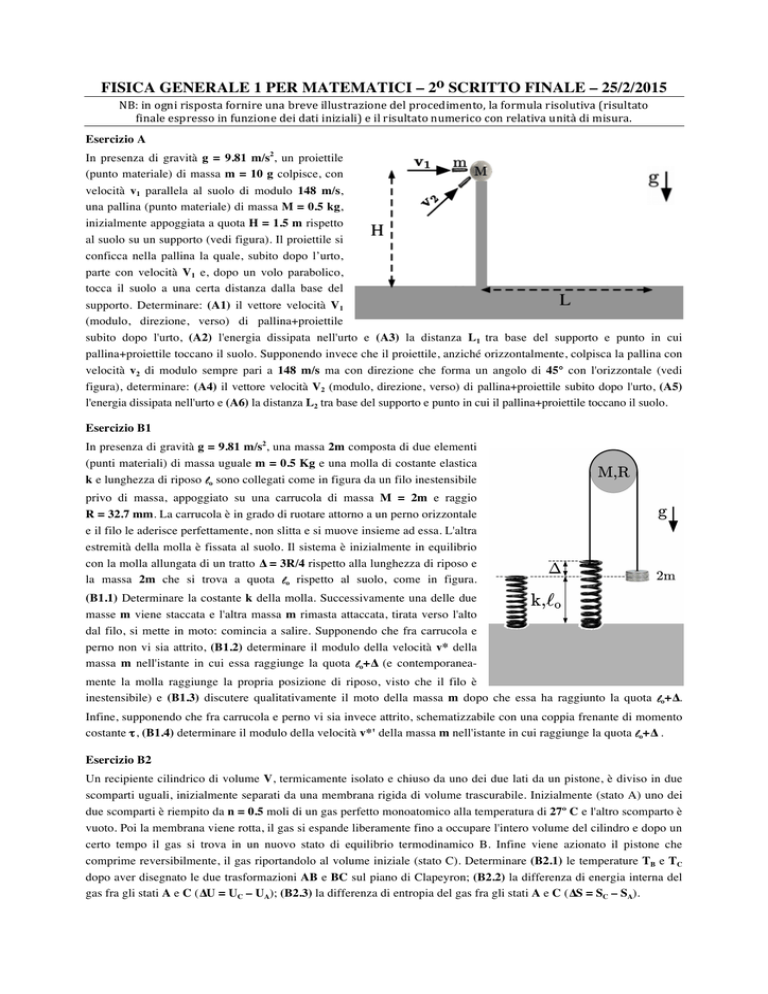
In presenza di gravità g = 9.81 m/s2, un proiettile
(punto materiale) di massa m = 10 g colpisce, con
velocità v1 parallela al suolo di modulo 148 m/s,
una pallina (punto materiale) di massa M = 0.5 kg,
inizialmente appoggiata a quota H = 1.5 m rispetto
al suolo su un supporto (vedi figura). Il proiettile si
conficca nella pallina la quale, subito dopo l’urto,
parte con velocità V1 e, dopo un volo parabolico,
tocca il suolo a una certa distanza dalla base del
supporto. Determinare: (A1) il vettore velocità V1
(modulo, direzione, verso) di pallina+proiettile
subito dopo l'urto, (A2) l'energia dissipata nell'urto e (A3) la distanza L1 tra base del supporto e punto in cui
pallina+proiettile toccano il suolo. Supponendo invece che il proiettile, anziché orizzontalmente, colpisca la pallina con
velocità v2 di modulo sempre pari a 148 m/s ma con direzione che forma un angolo di 45° con l'orizzontale (vedi
figura), determinare: (A4) il vettore velocità V2 (modulo, direzione, verso) di pallina+proiettile subito dopo l'urto, (A5)
l'energia dissipata nell'urto e (A6) la distanza L2 tra base del supporto e punto in cui il pallina+proiettile toccano il suolo.
Esercizio B1$
In presenza di gravità g = 9.81 m/s2, una massa 2m composta di due elementi
(punti materiali) di massa uguale m = 0.5 Kg e una molla di costante elastica
k e lunghezza di riposo l o sono collegati come in figura da un filo inestensibile
privo di massa, appoggiato su una carrucola di massa M = 2m e raggio
R = 32.7 mm. La carrucola è in grado di ruotare attorno a un perno orizzontale
e il filo le aderisce perfettamente, non slitta e si muove insieme ad essa. L'altra
estremità della molla è fissata al suolo. Il sistema è inizialmente in equilibrio
con la molla allungata di un tratto ∆ = 3R/4 rispetto alla lunghezza di riposo e
la massa 2m che si trova a quota l o rispetto al suolo, come in figura.
(B1.1) Determinare la costante k della molla. Successivamente una delle due
masse m viene staccata e l'altra massa m rimasta attaccata, tirata verso l'alto
dal filo, si mette in moto: comincia a salire. Supponendo che fra carrucola e
perno non vi sia attrito, (B1.2) determinare il modulo della velocità v* della
massa m nell'istante in cui essa raggiunge la quota l o+∆ (e contemporaneamente la molla raggiunge la propria posizione di riposo, visto che il filo è
inestensibile) e (B1.3) discutere qualitativamente il moto della massa m dopo che essa ha raggiunto la quota l o+∆.
Infine, supponendo che fra carrucola e perno vi sia invece attrito, schematizzabile con una coppia frenante di momento
costante τ, (B1.4) determinare il modulo della velocità v*' della massa m nell'istante in cui raggiunge la quota l o+∆ .
Esercizio B2
Un recipiente cilindrico di volume V, termicamente isolato e chiuso da uno dei due lati da un pistone, è diviso in due
scomparti uguali, inizialmente separati da una membrana rigida di volume trascurabile. Inizialmente (stato A) uno dei
due scomparti è riempito da n = 0.5 moli di un gas perfetto monoatomico alla temperatura di 27º C e l'altro scomparto è
vuoto. Poi la membrana viene rotta, il gas si espande liberamente fino a occupare l'intero volume del cilindro e dopo un
certo tempo il gas si trova in un nuovo stato di equilibrio termodinamico B. Infine viene azionato il pistone che
comprime reversibilmente, il gas riportandolo al volume iniziale (stato C). Determinare (B2.1) le temperature TB e TC
dopo aver disegnato le due trasformazioni AB e BC sul piano di Clapeyron; (B2.2) la differenza di energia interna del
gas fra gli stati A e C (∆U = UC – UA); (B2.3) la differenza di entropia del gas fra gli stati A e C (∆S = SC – SA).
FISICA GENERALE 1 PER MATEMATICI – 2o SCRITTO FINALE – 25/2/2015
Soluzione esercizio A
A1 L’urto è perfettamente anelastico, quindi per la conservazione della quantità di moto mv1 =
m
(m + M )V1 e quindi V1 = m+M
v1 = 2, 9 m/s; la direzione e il verso di V1 coincidono con quelli di
v1 . A2 L’energia dissipata è data dalla di↵erenza tra l’energia iniziale EI = 12 mv12 e quella finale
EF = 12 (m + M )V12 :
E = EI
EF = 107, 4 J. A3 Dopo l’urto il corpo pallina+proiettile compie
un moto parabolico partendo dalla posizione iniziale x(0) = 0, y(0) = H con velocità V0x = V1 ,
1 2
V0y = 0. Le equazioni che descrivono il moto sono: x(t) = V0x t e y(t) = y(0)
2 gt . Dalla
q
2H
seconda si ricava il tempo di volo tv =
g = 0, 55 s, che sostituito nella prima fornisce la distanza
L1 = V1 tv = 1, 60 m. A4 Come per il punto A1: V2 =
m
m+M v2
concidono con quelli di v2 . A5 Come per il punto A2:
= 2, 9 m/s, direzione e verso di V2
E = EI
EF = 107, 4 J. A6 In questo
caso la velocità iniziale è V0x = V2 cos ✓ = 2.05 m/s, V0y == V2 sin ✓ = 2, 05 m/s. Le equazioni che
descrivono
moto sono⌘quindi x(t) = V0x t e y(t) = y(0) + V0y t 12 gt2 , il tempo di volo è dato da
⇣ il q
V
tv = g0y 1 + 1 + 2gH
= 0, 8 s e la distanza L2 è pari a L2 = V0x tv = 1, 64 m.
V2
0y
Soluzione esercizio B1
B1.1 All’equilibrio la risultante delle forze agenti sulla massa composta dai due elementi è nulla e
quindi k
2mg = 0, da cui k = 2mg/ = 400 N/m. B1.2 In assenza di attrito l’energia meccanica
si conserva, quindi EI = EF con EI = 12 k 2 ed EF = mg + 12 mv ⇤2 + 12 I! 2 , dove I = 12 M R2
q
EI mg
e ! = v ⇤ /R. Si ottiene quindi v ⇤ =
== 0. B1.3 La massa m è soggetta alla forza
1
(m+ 1 M )
2
2
peso che la accelera verso il basso, man mano che la massa si muove la molla si allunga e quindi
applica tramite il filo una forza verso l’alto che cresce fino ad eguagliare la forza peso quando la
massa raggiunge l’altezza iniziale l0 ; il moto prosegue con oscillazioni della massa attorno a questa
posizione. Le due posizioni di equilibrio sono (
+ l0 ; 2
+ l0 ). B1.4 In presenza di attrito
l’energia iniziale del sistema non è sufficiente a far raggiungere alla massa la quota l0 +
.
Soluzione esercizio B2
B2.1 La prima trasformazione è un’espansione libera di un gas ideale, quindi TB = TA = 300
K. La seconda è una compressione adiabatica, quindi T V
( = 5/3). B2.2 Per la prima trasformazione
TB ) = n cV TA (2
UAB +
AB:
1
1
= cost. e TC = 2
UAB = 0 , per la seconda
TB = 476 K
UBC = n cV (TC
1) = 1097 J (cV = 3/2 R, R = 8, 314472 J/(K mol)). Quindi
UAC =
UBC = 1097 J. B2.3 Per la prima trasformazione calcolo l’entropia lungo l’isoterma
SAB = n R ln VVB
= 2, 88 J/K; per la seconda che è adiabatica
A
SAB +
1
SBC = 2, 88 J/K.
SBC = 0. Quindi
SAC =










