Impulso e Urti
Problema 1
Una palla da golf ha una massa di 5g. Calcolare l’impulso di un colpo che imprime alla palla la velocità di
50m/s. Se il bastone durante il colpo è stato in contatto con la palla per 5∙10-4s e la forza applicata è stata
costante, qual è stata intensità di tale forza?
Risoluzione:
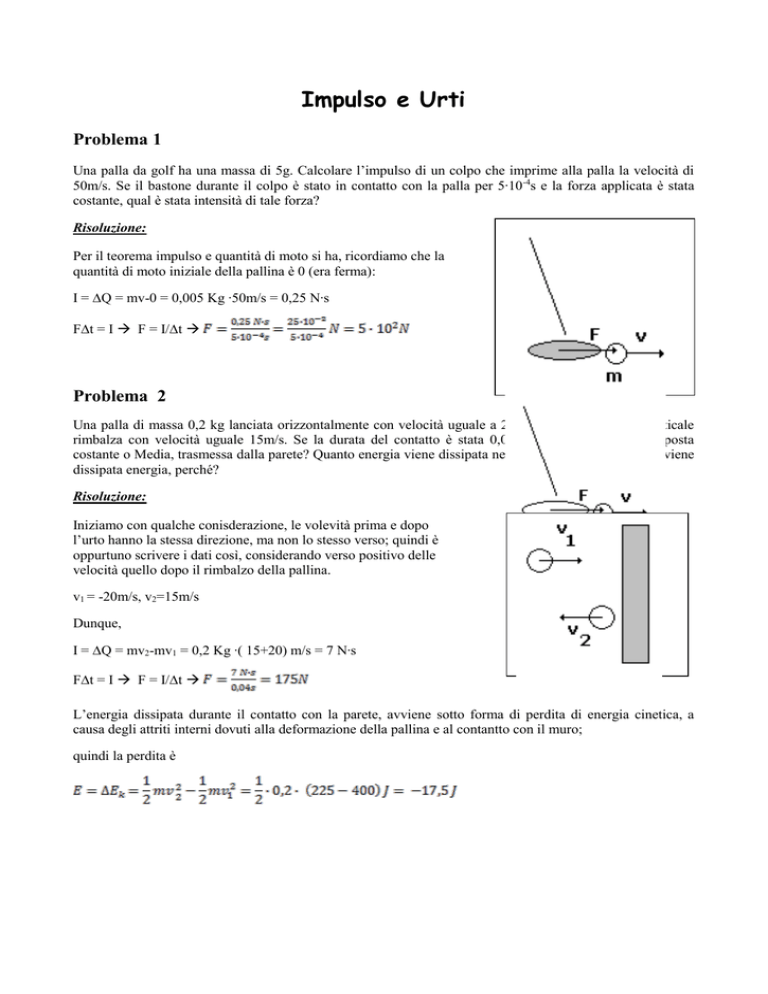
Per il teorema impulso e quantità di moto si ha, ricordiamo che la
quantità di moto iniziale della pallina è 0 (era ferma):
I = ∆Q = mv-0 = 0,005 Kg ∙50m/s = 0,25 N∙s
F∆t = I F = I/∆t
Problema 2
Una palla di massa 0,2 kg lanciata orizzontalmente con velocità uguale a 20m/s contro una parete verticale
rimbalza con velocità uguale 15m/s. Se la durata del contatto è stata 0,04s. Calcolare la forza, supposta
costante o Media, trasmessa dalla parete? Quanto energia viene dissipata nel contatto con la parete? Se viene
dissipata energia, perché?
Risoluzione:
Iniziamo con qualche conisderazione, le volevità prima e dopo
l’urto hanno la stessa direzione, ma non lo stesso verso; quindi è
oppurtuno scrivere i dati così, considerando verso positivo delle
velocità quello dopo il rimbalzo della pallina.
v1 = -20m/s, v2=15m/s
Dunque,
I = ∆Q = mv2-mv1 = 0,2 Kg ∙( 15+20) m/s = 7 N∙s
F∆t = I F = I/∆t
L’energia dissipata durante il contatto con la parete, avviene sotto forma di perdita di energia cinetica, a
causa degli attriti interni dovuti alla deformazione della pallina e al contantto con il muro;
quindi la perdita è
Problema 3
Un fucile spara una pallottola di massa 10g contro un blocco di massa 103g fissato a una molla. La pallottola
rimane incastrata nel blocco e la molla subisce una compressione di 5cm. Se la costante elastica della molla è
25 N/m, calcolare:
1.
2.
3.
4.
L’energia elastica massima della molla
La velocità del sistema blocco + pallottola subito dopo l’urto
La velocità della pallottola prima dell’urto
L’energia dissipata nell’urto. Perché?
Risoluzione:
Osserviamo il grafico, che distingue le tre fasi salienti del
fenomeno.
I dati: m=0,01Kg M = 1Kg x=0,05m k=25N/m
1) L’energia elastica massima si ha nel punto di massima compressione,
2) Per ottenere la velocità subito dopo l’urto bisogna cambiare
prospettiva. Si pensi invece all’energia cinetica che il corpo bloccopallottola ha in questo momento, e tale energia viene trasformata in
energia elestica durante la compressione della molla, dunque
3) Per questa domanda bisogna far ricorso al concetto di urto anelastico,
utilizzando il principi di conservazione della quantità di moto.
mv1 + Mv2 = (m+M)v mv1 + 0 = (m+M)v
4) Calcoliamo la variazione di energia cinetica, dovuta alla perdita i energia per produzione di calore
(energia termica),












