A. Chiodoni – esercizi di Fisica II
SECONDA LEZIONE: lavoro elettrico, potenziale elettrostatico, teorema di
Gauss (prima parte)
Esercizio 1
Tre cariche q1=q2=q3=q sono poste ai vertici di un triangolo equilatero di lato l,
calcolare (a) il potenziale elettrostatico al centro del triangolo, (b) l’energia
potenziale elettrostatica del sistema, (c) il lavoro W necessario per portare una
carica q0 posta al centro del triangolo all’infinito .
-> Soluzione
(a) Il potenziale al centro del triangolo sarà dalla somma dei potenziali delle tre
coniche uguali. Quindi, poiché
r=
l
1
l
⋅
=
o
2 cos 30
3
Il potenziale sarà dato da
V = 3⋅
q
4πε 0 r
=
⎛
qi
⎜⎜V = ∑ Vi = ∑
i
i 4πε 0 ri
⎝
3 3⋅q
4πε 0 l
(b) Poiché Ue (sistema ) =
qi q j
1
∑
2 i ≠ j 4πε 0 rij
⎞
⎟⎟
⎠
(il termine 1/2 davanti la sommatoria tiene
conto del fatto che ciascuna combinazione viene contata 2 volte).
Ue( sistema) = U 12 + U 13 + U 23 =
qq
q q
q1 q 2
+ 1 3 + 2 3
4πε 0 r 4πε 0 r 4πε 0 r
(c) La carica q0 posta al centro del triangolo possiede l’energia potenziale
elettrostatica:
1
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Ue(q 0 ) =
q1 q 0
q q
qq
+ 2 0 + 3 0
4πε 0 r 4πε 0 r 4πε 0 r
con
r=
l
3
L’energia potenziale elettrostatica complessiva è:
Ue = Ue( sistema) + Ue(q 0 )
Il lavoro necessario per allontanare la carica q0 è
w = − ∆Ue = −(∆Ue( sistema) − ∆Ue(q 0 ) ) = − ∆Ue(q 0 ) = Ue(q 0 )
in quanto ∆Ue(sistema)=0 perché l’energia potenziale del sistema rimane costante al
variare della posizione di q0 e l’energia potenziale all’infinito Ue(q0, ∞)= 0.
Esercizio 2
Una carica q è distribuita uniformemente su un sottile anello di raggio R. Calcolare il
potenziale sull’asse dello anello.
dl
-> Soluzione
q
la densità lineare di carica. La carica infinitesima in ciascun tratto
2πR
dl di anello è dq = λdl .
Definiamo λ =
Il potenziale sarà dato da:
dV =
1
4πε 0
⋅
dq
1 λdl
1 λ
=
⋅
=
⋅ dl
r
4πε 0 r
4πε 0 r
e allora
λ ⋅ 2πR
1 λ
q
, in quanto r 2 = R 2 + x 2
V =
⋅ ∫ dl =
=
2
2
4πε 0 r l
4πε 0 r
4πε 0 R + x
2
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Il potenziale è massimo nel centro O e decresce all’aumentare della distanza di P dal
q
centro. Per x >> R, V =
, come se la carica fosse nel centro. Possiamo calcolare il
4πε 0 x
campo elettrico come gradiente del potenziale:
Ex = −
q ∂ 2
∂V
R + x2
=−
∂x
4πε 0 ∂x
Ey = −
∂V
=0
∂y
(
,
Ez = −
)
−1 / 2
=
(
q⋅x
4πε 0 ⋅ R 2 + x 2
)
3/ 2
∂V
=0
∂z
Esercizio 3
Un sottile disco di raggio R ha una carica q distribuita uniformemente su tutta la sua
superficie; calcolare il potenziale.
dr, dq
l
R
θ
x
r
P
x
->Soluzione
q
; ciascun elemento di superficie di
πR 2
area dS possiede una carica dq = σ ⋅ dS . Consideriamo un anello concentrico al disco di
Definiamo la densità di carica superficiale σ =
raggio compreso tra r ed r+dr e area dS = 2πr dr . Il potenziale sarà dato da
dV =
dq
4πε 0 l
=
σdS
4πε 0 x + r
σ
-> V = ∫ dV =
4ε 0
S
2
R
∫
0
2
=
2rdr
x +r
2
2
σ 2πrdr
4πε 0 x + r
2
=
σ
⋅
2ε 0
(R
2
2
=
σ
rdr
⋅
2ε 0
x2 + r 2
)
+ x2 − x ,
3
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
(per risolvere l’integrale, si è proceduto come segue: la regola generale di integrazione
x m +1
m
per le potenze dice che ∫ x dx =
, m ≠ −1
m +1
x = (x 2 + r 2 )
R
R
⎡ ( x 2 + r 2 )1 / 2 ⎤
2
2 −1 / 2
, allora ∫ (r + x ) (2r )dr = ⎢
m = −1 / 2
⎥
1/ 2
⎣
⎦0
0
dx = 2rdr
se poniamo
e dunque
σ
V=
4ε 0
R
∫
0
2rdr
x2 + r 2
=
[
σ
⋅ 2 (x 2 + r 2 )
4ε 0
]
R
0
=
σ
2ε 0
( (x
2
Per x = 0, cioè al centro dell’anello, si ha che V max =
per x >> R -> V =
q
)
+ r2) − x )
σR
;
2ε 0
(come se la carica fosse tutta nel centro)
4πε 0 x
Calcoliamo il campo elettrostatico come gradiente del potenziale:
⎛
x
⎜1 −
⎜
2
R + x2
⎝
della prima lezione)
Ex = −
σ
∂V
=
∂x 2ε 0
⎞
⎟
⎟
⎠
,
E y = Ez = 0
(come già trovato nell’esercizio 6
Esercizio 4
Un guscio sferico di raggio a porta una distribuzione di carica continua uniforme
avente densità di carica superficiale σ . Calcolare il campo elettrico generato da tale
distribuzione di carica in un punto qualsiasi P esterno al guscio stesso, sia V(R = ∞ ) = 0
-> Soluzione
O
4
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Si può suddividere il guscio sferico in tante “rondelle” ognuna delle quali possiede una
carica
dq = σdA , dove dA è l’area infinitesima individuata dal prodotto della
circonferenza della rondella per il suo spessore.
Quindi: dq = σ ⋅ dA = σ 2π (a sin θ ) ⋅ a{
dθ (a sinθ è il raggio della “rondella”)
14243
circonferenza rondella
arcoAA '
Nel punto P il potenziale infnitesimo generato della carica dq è:
dV =
1
4πε 0
⋅
dq
1 2πa 2
=
⋅
σ sin θ dθ + cos t
r
4πε 0
r
Considerando il triangolo ACP, per il teorema di Carnot:
r 2 = a 2 + R 2 − 2 Ra cos θ
derivando rispetto a r e a θ:
2rdr = −(2 Ra sin θ )dθ
e quindi
dV =
1
4πε 0
->
⋅
sin θ dθ dr
=
r
aR
2πσ ⋅ a
dr + cos t
R
dove cost = 0 se V = 0 a R = ∞ .
Integrando su tutto il guscio:
V =
1
4πε 0
⋅
2πσ ⋅ a OP + 2 a
1 4πσ ⋅ a 2
1
q
dr
=
⋅
=
⋅
∫
OP
R
4πε 0
R
4πε 0 R
Dove q è la carica totale distribuita sul guscio q = σ 4π ⋅ a 2 .
Il campo elettrico ha simmetria radiale rispetto al centro del guscio:
∂V
1 4πσ ⋅ a 2
1
q
=
⋅
=
⋅ 2
Er = −
2
∂r 4πε 0
4πε 0 R
R
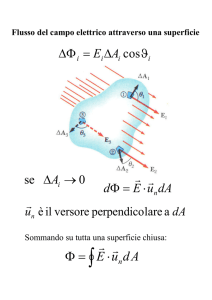
Determiniamo ora il campo elettrico utilizzando il teorema di Gauss:
5
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Il campo elettrico è radiale in quanto dato da contributi simmetrici a due a due
rispetto all’asse x, la risultante è dunque radiale. Il campo elettrico ha modulo
constante sul guscio ed ha verso entrante o uscente a seconda del segno della carica.
r
E = E (r ) uˆ r ,
(r = distanza dal guscio a P)
Applichiamo il teorema di Gauss:
r
r r
φ ( E ) = ∫ E ⋅ u n dS = ∫ E (r ) ⋅ uˆ r ⋅ uˆ n dS = E (r ) ∫ dS =E (r ) ⋅ 4πr 2 =
qint
ε0
, dove q int = 4πa 2σ
quindi
E (r ) =
4πa 2σ
a 2σ
q
=
=
2
2
4πr ε 0 r ε 0 4πr 2 ε 0
()
->
r
E=
q
4πε 0 r 2
uˆ r
r
All’interno del guscio, φ E = E S ' , dove S’ è il guscio sferico di raggio r < a. All’interno
()
del guscio non c’è carica, cioè E = 0 e dunque φ E = 0 .
Cosa succede al tendere di r ad a?
Dall’interno il campo è sempre nullo ( lim r − > a − E (r ) = 0 ), mentre lim r − > a +
σ
a 2σ
=
2
r ε0 ε0
->
punto discontinuità
6
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Per il potenziale V =
q
4πε 0 r
se r = a ,
V =
q
4πε 0 a
a
Esercizio 5
r
Un elettrone viene immesso con velocità v0 in una regione limitata in cui agisce un
r
campo elettrostatico uniforme perpendicolare a v0 . Uscito della regione l’elettrone
colpisce uno schermo S nel punto C. Calcolare l’angolo di deflessione α , l’energia
cinetica e la velocità finali dell’elettrone e la distanza d del punto C dall’asse x.
y
-> Soluzione
Scriviamo l’equazione del moto dell’elettrone:
eE
diretta lungo
m
l’asse y quando attraversa la regione in cui c’è campo elettrostatico. Il moto lungo x è
r
rettilineo uniforme con velocità v0 , il moto lungo y è uniformemente accelerato.
Fe=F cioè eE=mea. L’elettrone è soggetto a una accelerazione a =
7
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
1 eE 2 1
⋅
t = ⋅ at 2 .
2 m
2
La traiettoria dell’elettrone entro la regione di campo elettrostatico è un arco di
parabola (curva rossa nel disegno) di equazione
Le equazioni del moto lungo i due assi cartesiani sono: x = v 0 t , y =
1 eE x 2
y ( x) = ⋅
2 m v0 2
L’angolo di deflessione si calcola da:
eEl
⎛ dy ⎞
tgα = ⎜ ⎟ =
(la derivata di una funzione f in un punto x0 è la misura del
2
⎝ dx ⎠ x =l mv0
coefficiente angolare, cioè la tangente dell'angolo)
e la distanza h tra il punto in cui l’elettrone esce dalla zona di campo elettrico e l’asse
1 eE l 2
x sarà: h = y (l ) = ⋅
2 m v0 2
L’energia cinetica in B sarà data dall’energia cinetica iniziale più l’energia potenziale
acquistata nel passaggio della zona di campo elettrico:
1
1
1
e 2 E 2l 2
2
2
⋅ mv 2 = ⋅ mv 0 + E e h = ⋅ mv0 +
2
2
2
2
2mv0
Moltiplicando per due e dividendo per m:
v 2 = v0 +
2
e 2 E 2l 2
2
m v0
2
= v 0 + 2ah e quindi la velocità finale è v = v02 + 2ah .
2
Fuori dalla zona di campo elettrico, l’elettrone descrive una traiettoria rettilinea;
calcoliamo d:
d = h + L ⋅ tgα =
e E l ⎛1
⎞
+ L⎟
2 ⎜
mv 0 ⎝ 2
⎠
Questo è il principio di funzionamento di un tubo a raggi catodici.
Esercizio 6
Un elettrone entra con velocità v 0 = 10 7 m / s in una regione di lunghezza l = 4cm in cui
agisce un campo elettrico E = 10 4 V / m uniforme e perpendicolare a v0 . Calcolare (a) lo
spostamento d dopo l’attraversamento e (b) l’energia cinetica acquisita ∆E (in eV).
8
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
-> Soluzione
(a) Le equazioni del moto dell’elettrone sono:
eE
diretta lungo
m
l’asse y quando attraversa la regione in cui c’è campo elettrostatico. Il moto lungo x è
r
rettilineo uniforme con velocità v0 , il moto lungo y è uniformemente accelerato.
Fe=F cioè eE=ma. L’elettrone è soggetto a una accelerazione a =
Le leggi orarie lungo gli assi cartesiani sono:
x = v0t
1
1 qE 2
y = ⋅ at 2 = ⋅
t
2
2 m
La traiettoria dell’elettrone sarà dunque
y=
1 eE x 2
⋅
2 me v0 2
A questo punto, è possibile determinare d:
d = y (l ) =
1 eE l 2
1 1.6 ⋅ 10 −19 ⋅ 10 4 ⋅ 16 ⋅ 10 −4
⋅
=
⋅
= 1.4cm = 0.014m
2 me v 0 2 2
9.1 ⋅ 10 −31 ⋅ 10 7
(b) Come visto nell’esercizio precedente
v 2 = v0 + 2ad
2
v = v0
2
2
eE
2 ⋅ 1.6 ⋅ 10 −19 ⋅ 10 4 ⋅ 0.014
14
d = 1 ⋅ 10 +
= 1 ⋅ 1014 + 0.49 ⋅ 1014 = 1.49 ⋅ 1014 m 2 / s
+2
−31
m
9.1 ⋅ 10
9
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE
A. Chiodoni – esercizi di Fisica II
Quindi, l’energia cinetica finale è Ef =
(
1
1
me v 2 = ⋅ 9.1 ⋅ 10 −31 ⋅ 1.49 ⋅ 1014
2
2
)
2
= 6.79 ⋅ 10 −17 J
Infine, l’energia acquisita è pari a
∆E = Ef − Ei =
1
2
me (v 2 − v 0 ) = eEd = 2.24 ⋅ 10 −17 J = 140eV
2
Esercizio 7
Con il riferimento alla figura, q1 = q = -10-8C e il flusso del campo elettrostatico E
attraverso le superfici indicate S1, S2 e S3 risulta: φ S1 (E ) = φ S 2 (E ) = 0 ,
φ S (E ) = 2.26 ⋅ 10 3 Vm . Calcolare q2 e q3.
3
S3
S2
S1
-> Soluzione
Calcoliamo il flusso del campo E attraverso le tre diverse superfici, utilizzando il
teorema di Gauss:
φ S (E ) =
q1 + q 4
φ S (E ) =
q 2 + q3
φ S (E ) =
q1 + q3
1
2
3
ε0
ε0
ε0
=0
->
q1 = −q 4 = 10 −8 C
=0
->
q 2 = −q3
= 2.26 ⋅ 10 3
Quindi, possiamo ora determinare le due cariche incognite.
(
)
(
)
q 3 = ε 0 2.26 ⋅ 10 3 − q1 = 8.8 ⋅ 10 −12 ⋅ 2.26 ⋅ 10 3 + 10 −8 = 3 ⋅ 10 −8 C
q 2 = − q 3 = −3 ⋅ 10 −8 C
10
Corsi a distanza – corso di laurea in INGEGNERIA LOGISTICA E DELLA PRODUZIONE