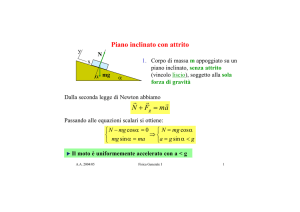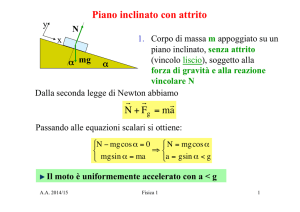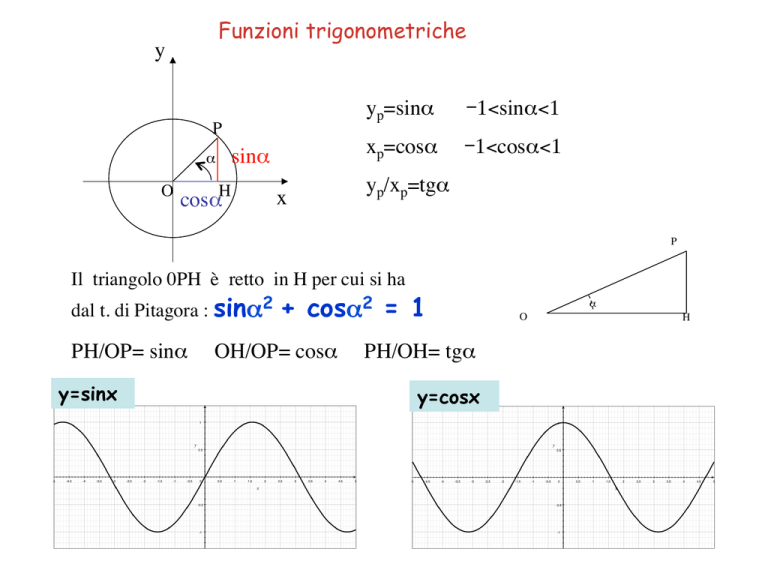
Funzioni trigonometriche
y
P
sinα
α
O
H
cosα
x
yp=sinα
-1<sinα<1 xp=cosα
-1<cosα<1 yp/xp=tgα
P
Il triangolo 0PH è retto in H per cui si ha dal t. di Pitagora : sinα2
PH/OP= sinα
y=sinx
+ cosα2 = 1
OH/OP= cosα
PH/OH= tgα
y=cosx
O
α
H
€
y
y = senα
+1
ο
€ –1
90°
180°
270°
360°
π/
2
π
y = cosα
3
π/
2
2
π
5
π/
2
3
π
radianti
senα=cos(α-90o)
α
y=tagx
Periodicità
Le funzioni sinx e cosx sono periodiche con periodo 2π , la funzione tagx è
periodica con periodo π Simmetria
sin(-x)=-sinx
antisimmetria rispetto all’asse y ( x=0)
cos(-x)=cosx
simmetria rispetto all’asse y (x=0)
tag(-x)=-tagx
antisimmetria rispetto all’asse y ( x=0)
Alcune relazioni tra queste funzioni trigonometriche cos x = sin(x +
π
)
2
sin x
cos x
(cos x)2 + (sin x)2 = 1
tagx =
Il valore medio della funzione sinx e cos x in un intero periodo è 0 perché per ogni
valore positivo vi è un corrispondente valore negativo .
Sono funzioni periodiche anche sin2x e cos2x e in un periodo (2π) il loro valor
medio è 1/2 come si può vedere dal grafico
1
sin2x
0.5
0
-0.5
-1
0
1
2
x
3
4
5
6
7
1
0.5
2
cos x
cos2x
0
-0.5
-1
0
1
2
3
4
x
5
6
7
La funzione y=sinx cosx ha periodo π e il valor medio è 0
1
sinx cosx
0.5
0
-0.5
-1
0
1
2
3
x
4
5
6
7
Per un angolo α piccolo (minore di 0.1rad) con buona approssimazione potremmo
scrivere: sinα≈tgα ≈α e cosα ≈1
Altre relazioni sin(α+β)=sinα cosβ+cosα sinβ
• Disegnare il grafico di y=sin2x, y=2+sinx
• La velocità di propagazione del suono è di circa (onda che si propaga y=sin(kx-ωt))
340m/s in aria
1450m/s in acqua 5000m/s nel ferro
Si calcoli le lunghezze d’onda nei tre mezzi di un onda sonora di frequenza ν=440Hz e di
un onda di un ultrasuono di frequenza ν=5MHz.
y=sin2x
1
Periodo π
y
0.5
0
-0.5
-1
0
0.5
1
1.5
2
x
2.5
3
3.5
y=2+sinx
Data
1
3
Periodo 2π
y
2.5
2
1.5
1
0
1
2
3
4
x
5
6
7
8
Periodo e Frequenza
Il Moto di una molla, di un pendolo ecc. si ripetono periodicamente nel tempo.
y = Asenα = Asen(ωt)
€ 2π
ω (t + T) − ωt = 2π → ωT = 2π → ω =
T
ω = Pulsazione
= 2πν
T = Periodo
ν = 1/T Frequenza