Piano inclinato con attrito

Piano inclinato con attrito
y
N
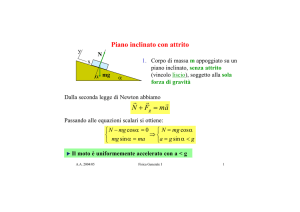
1.  Corpo di massa m appoggiato su un
piano inclinato, senza attrito
(vincolo liscio), soggetto alla
α
mg α
forza di gravità e alla reazione
vincolare N
Dalla seconda legge di Newton abbiamo
x
 

N + Fg = ma
Passando alle equazioni scalari si ottiene:
€
⎧N − mg cos α = 0 ⎧ N = mg cos α
⇒ ⎨
⎨
⎩ mgsin α = ma
⎩a = gsin α < g
"   Il moto è uniformemente accelerato con a < g
A.A. 2014/15
€
Fisica 1
1
2.  Ora consideriamo il caso in cui c’è attrito tra il corpo ed il piano
inclinato (vincolo scabro), affinché il corpo stia fermo deve
essere
 max  
N
Fs
Fs + N + Fg ≤ 0
y
α
mg
α
⎧−F max + mgsin α ≤ 0
⎨ s
⎩N − mg cos α = 0
x
Fsmax = µ s N
mgsinα ≤µ sN =µ s mgcosα
€
La reazione vincolare ha due componenti una verticale (N) ed una
orizzontale
costituita dalla forza di attrito statico (Fs).
€
Dalla relazione precedente si ottiene che il corpo è in equilibrio
statico se
tgα ≤ µ s
A.A. 2014/15
Fisica 1
2
Quando il corpo si muove si ha

 

Fd + N + Fg = ma
mgsinα−µdmgcosα=ma
a= sinα−µ cosα g
⎧N − mg cos α = 0
⎨
⎩−Fd + mgsin α = ma
Fd = µ d N
⎛
⎜
⎜⎜
⎝
d
⎞
⎟
⎟⎟
⎠
sinα−µd cosα>0
€
µd <tgα
€
Se µd = tgα ⇒ a = 0 ⇒moto è uniforme ⇒c’è equilibrio dinamico
€
A.A. 2014/15
Fisica 1
3
Riassumendo
perα ≤ α s
∴Il corpo resta fermo
tgα s = µ s
perα > α s
∴ Il corpo scende
α può diminuire ed essere inferiore ad α s ;
per α d < α < α s dove α d /tgα d = µ d si ha
∴ Il corpo si muove di moto uniformemente accelerato se
tgα > µ
d
∴ Il corpo prosegue con v 0 se
tgα = tgα d = µ
d
∴ Il corpo si muove con v 0 ,si ferma se
mgsinα < µ mg cos α ⇒ tgα < µ
d
d
A.A.
€2014/15
Fisica 1
4