Esercizio 1

ESERCITAZIONE DEL 13 GIUGNO 2007
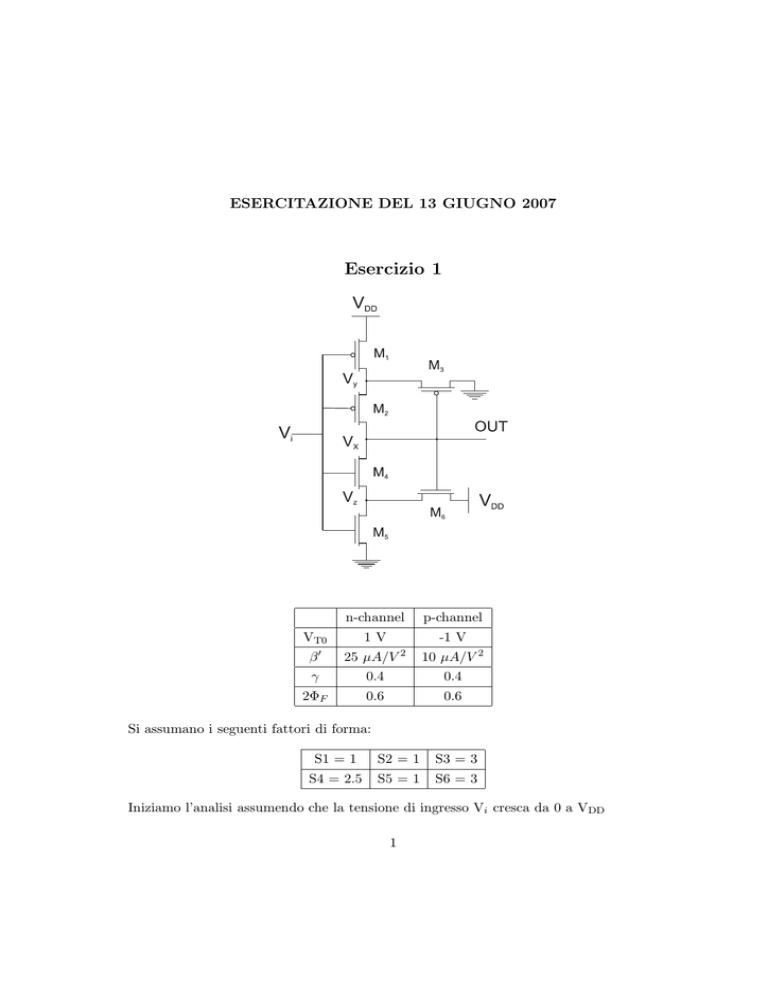
Esercizio 1
n-channel
p-channel
VT0
1V
-1 V
β′
25 µA/V 2
10 µA/V 2
γ
0.4
0.4
2ΦF
0.6
0.6
Si assumano i seguenti fattori di forma:
S1 = 1
S2 = 1
S3 = 3
S4 = 2.5
S5 = 1
S6 = 3
Iniziamo l’analisi assumendo che la tensione di ingresso Vi cresca da 0 a VDD
1
Corso di Circuiti Elettronici Digitali LA
2
1. Per Vi = 0
M1 ed M2 sono accesi e Vx = Vy = 5 V.
Al tempo stesso M4 e M5 sono spenti. M3 è OFF mentre M6 è ON ed opera in
saturazione con corrente nulla:
1 ′
β S6 (VDD − VZ − VT6 )2 = 0
2 n
p
p
= VT0 + γ( 2ΦF + VZ − 2ΦF )
I6 =
VT 6
VZ
= VDD − VT 6 = 3.5V
Vout = 5V
2. Per Vi = 1V
M1 ed M2 sono ON. M5 è alla soglia della conduzione. M4 è OFF, per cui
VZ = 3.5V
Vout = VDD = 5V
3. Per Vi =2V
M1, M2 ed M5 sono ON. M6 è acceso e opera nella regione di saturazione. Per M4
non possiamo dirre nulla per cui ipotizziamo che sia OFF ed M5 saturo. Come
conseguenza
I6 = I5
1 ′
1 ′
βn S5 (Vi − VTN0 )2 =
β S6 (VDD − Vz − VTn )2
2
2 n
Ricordando che M5 soffre di effetto body, si ottiene che
Vz = 2.976V.
Verfichiamo ora se la scelta di M4 spento è ben posta:
VGS (M 4) = Vi − Vz = −0.98 < VT0 ⇒ M 4 OFF
4. Per Vi =3.5V
Vz continua a diminuire. M1, M5 sono ON. Anche M6 è ON ed opera in saturazione. Facciamo le seguenti ipotesi: M4 OFF, M5 ON operante in zona lineare,
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
3
mentre M6 on e saturo. Con questa scelta:
I5 = I6
1 ′
1 ′
β S5 [2(Vi − VTn0 )Vz − Vz2 ] =
β S6 (VDD − Vz − VT6 )2
2 n
2 n
Risolvendo in Vz si ottiene
Vz = 2.2 V
Verifichiamo l’ipotesi si M4
VGS (M 4) = Vi − Vz = 3.5 − 2.2 = 1.3 > VT0 ⇒ M 4 ON
M4 è ON, per cui l’analisi fatta in precedenza non è piú valida e la tensione del
nodo x è 0.
Ciò è dovuto all’innesco di una retroazione positiva che coinvolge i transistori
M4 ed M6. Infatti se M4 conduce, tenderà ad abbassare la tensione del nodo di
uscita. Dato che M6 è in configurazione a Drain comune, la tensione al nodo x
tenderà a seguirla. Come conseguenza aumenta la tensione VGS del transistore
M4. Dato che la sua corrente non può aumentare più di tanto visto che è vincolata
del transistore M5, dovrà abbassarsi la sua tensione di drain e dunque V0 .
Si conclude che la soglia logica superiore Vth + è approssimativamente 3.5 V.
Tale tensione dipende esclusivamente dal rapporto dei fattori di forma di M6 ed
M4.
5. Per Vi =5V
M4 ed M5 sono ON e Vx è 0. I pMOS M1 ed M2 sono sicuramente spenti mentre
M3 opera in saturazione, cosı́:
IDS (M 3) = 0
1 ′
IDS (M 3) =
β S3 (−Vy − VTp )2 = 0
2 p
p
p
VTp = VTp0 − γ( 2ΦF + Vy − 2ΦF )
Vy = 1.5V
Vout = 0
6. Per Vi = 4V
M1 è alla soglia della conduzione, M2 è OFF mentre M3 opera in saturazione.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
4
L’uscita non cambia
7. Per Vi = 3V
M1 è ON ed opera in saturazione, come M3.
Ipotizziamo M2 OFF:
IDS (M 1) = IDS (M 3)
1 ′
1 ′
β S1 (Vi − VDD − VT p0 )2 =
β S3 (−Vy − VTp )
2 p
2 p
Vy = 2.02V
VGS (M 2) = Vi − Vy = −0.98 > VT 0 > M 2 OFF
8. Per Vi =1.5
M1 è ON ed opera in regione lineare, mentre M3 è saturo:
IDS (M 1) = IDS (M 3)
1 ′
1 ′
β S1 (2(Vi − VDD − VT p0 )(Vy − VDD ) − (Vy − VDD )2 ) =
β S3 (−Vy − VDD )2
2 p
2 p
Vy = 2.79V
Con tale valore di Vy il transistore M2 deve essere già acceso. Come conseguenza
l’uscita si porta a VDD .
Come nel caso precedente questo è dovuto all’innesco una retroazione positiva
che coinvolge i transistori M1 ed M3, che porta all’innesco del circuito.
Si può dunque assumere la tensione di soglia logica bassa Vth - approssimativamente pari a 1.5 V e dipende esclusivamente dali fattori di forma dei transistori
M1 ed M3.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
5
Esercizio 2
1. Assumendo la configurazione VA =VB =0, VC =VDD , V D =0 determinare la tensione ad ogni nodo.
VX
VDD
VY
VDD − VTN
VZ
Alta impedenza
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
6
2. A partire dalla configurazione indicata nel punto precedente, si consideri ora la
transizione istantanea di VA da 0 a VDD . Determinare la tensione ad ogni nodo
a transitorio esaurito
VX
VDD
VY
VDD − VTN
VZ
0
3. A partire dalla configurazione VA =VD , V B =0, VC =VDD , VD =0 si consideri la
transizione istantanea di VA da VDD a 0 e VB da 0 a VDD . Determinare la
tensione ad ogni nodo a transitorio esaurito.
VX
VDD
VY
VDD − VTN
VZ
VDD − VTN
4. A partire dalla configurazione indicata nel punto precedente, si consideri ora la
transizione istantanea di VD da 0 VDD e VA da 0 a VDD . Determinare la tensione
ad ogni nodo a transitorio esaurito.
A.A. 2006/2007
VX
0
VY
0
VZ
0
Corso di Circuiti Elettronici Digitali LA
7
Esercizio 3
VDD
2.5 V
VT N
0.5 V
βn
100 µA/V 2
λ
0
Φf
0.6 V
γ
0.2 V1/2
Con riferimento al circuito in figura, assumendo S(MM N 1 )=4, R1 =150 KΩ, R2 =100
KΩ, R3 =50 KΩ, I0 =10µA, si risponda ai seguenti quesiti:
1. Determinare i valori delle tensioni Vi e Vo nel punto di riposo
Vi = VDD
R3
= 0.625 V
R3 + R1
Si faccia l’ipotesi di MM N 1 saturo. Si ottiene
ID + I0 =
VDD − V0
R2
1
VDD − V0
βn (Vi − VTN )2 + I0 =
2
R2
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
8
da cui si ottiene
V0 = 1.1875
che è consistente con l’ipotesi di nMOS saturo fatta.
2. Si scriva l’espressione analitica ed il valore numerico dei parametri differenziali
nel punto di lavoro calcolato in precendenza
gm = βn′ Sn (Vi − VTN ) = 50µA/V
gd = 0
gmb = 2√2Φ γ +V gm = 0.13gm = 5.45µA/V
F
SB
3. Si disegni il circuito ai piccoli segnali nel punto calcolato precedentemente
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
9
Esercizio 4
VDD
2.5 V
VT N
0.5 V
βn′
100 µA/V 2
λ
0
Φf
0.6 V
γ
0.2 V1/2
Cox
4 fF/µm2
Con riferimento al circuito in figura e alle forme d’onda in figura graficare qualitativamente l’andamento della tensione Vx . Si considerino già esauriti i transitori agli istanti
di tempo t1, t2, t3.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
10
Esercizio 5
Con riferimento al circuito in figura, considerando I0 = 20 µA
1. Trascurando l’effetto di modulazione di canale e quello body per entrambi i transistori, determinare il valore del tensione V0 considerando Vi =1V.
Il transistore MN1 lavora sicuramente in saturazione. Ipotizziamo che anche MN2
lavori in saturazione:
ID(M N 1) = ID(M N 2)
1 ′
1 ′
βn S1 (VDD − V0 − VTN )2 =
β S2 (Vi − VTN )2 + I0
2
2 n
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
11
da cui si ottengono i valori:
V0 = 1.59 V, 2.4 V
Il secondo valore non è corretto perchè trattandosi di un invertitore a carico
saturo, la tensione VOH è pari a VDD -VTN =2V. Con V0 pari a 1.59 V il transistore
MN2 è effettivamente in saturazione.
2. Calcolare l’espressione analitica ed il valore numerico dei parametri differenziali
dei transistori nel punto di lavoro precedente senza trascurare l’effetto body
ma trascurando la modulazione di canale.
gm (M N 1)
gm (M N 2)
gd (M N 1)
gd (M N 2)
gmb (M N 1)
=
=
=
=
=
βn′ S1 (VDD − V0 − VTN ) = 161µS
βn′ S2 (Vi − VTN ) = 50µS
0
0
√ γ
gm (M N 1) = 10.8µS
2 Φ +V
gmb (M N 2)
=
√γ g (M N 2)
2 ΦF m
F
SB
= 6.45µS
3. Disegnare i circuito equivalente ai piccoli segnali e calcolare il guadagno di tensione Av = vvoi , considerando i parametri differenziali calcolati nel punto precedente.
Av =
vo
gm (M N 2)
=−
vi
gm (M N 1) + gmb (M N 2)
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
12
Esercizio 6
VDD
2.5 V
VT 0
0.5 V
βn′
100 µA/V
2.5 V
0.5 V
2
50 µA/V 2
λ
0
0
Φf
0.6 V
0.6 V
γ
Cox
0.2
V1/2
4 fF/µm2
0.2 V1/2
4 fF/µm2
1. Calcolare il valore minimo della tensione VS che garantisce il funzionamento del
tansistore MN2 in saturazione.
I transistori MN1 e MP1 formano un invertitore CMOS pienamente complementare polarizzato sulla soglia logica VTL =VX :
p
√
βp (VDD + VTp ) + βn VTn
p
VTL =
= 0.891 V
√
βp + βn
Il transistore MN2 è saturo se VDS >VGS -VTN , quindi:
VS > 0.891 − 0.5 = 0.391 V
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
13
2. Un difetto nel processo tecnologico porta ad una variazione del valore della resistenza R. Indicare in che modo tale variazione modifica il valore della tensione
VS calcolato nel punto precedente.
Essendo nulla la corrente di gate dei transistori, la resistenza R non modifica il
valore della tensione.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
14
Esercizio 7
Con riferimento al circuito in figura e assumendo le seguenti condizioni iniziali:
VOUT = VDD = 2.5V
VZ = VY = 0V
VA = VB = 0V
si calcoli il valore finale di tensione ai nodi Y, Z, OUT in seguito alla transizione
dell’ingresso VA da 0 a VDD . Si consideri γn = 0.
M2 rimane spento: non si crea nessun cammino conduttivo attraverso cui si possa
caricare/scaricare la capacità CY . Quindi VY,fin = VY,in = 0.
Il valore finale di tensione ai nodi OUT e Z si trova imponendo la conservazione della
carica. La condivisione di carica si interrompe in seguito a due possibili eventi:
• MN1 è acceso con VDS nulla, ovvero quando Vz =Vout
• MN1 si spegne perchè VGS ≤VTN , ovvero se VZ,fin =VTN =2V.
Quale delle due condizioni si verifica prima dipende dal rapporto tra le due capacità
C1 e CZ.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
15
Ipotizziamo che sia vero il primo caso. Applichiamo la legge di conservazione della
carica:
C1VOUT,in = C1VOUT,fin + C2VZ,in
C1VDD = C1VOUT,fin + 0.1C1VZ,fin
da cui si ottiene VZ,fin =VOUT,fin =2.27 V. Questa ipotesi non è però corretta, dato che
per questo valore di VZ , MN1 deve essere già spento. Per cui l’ipotesi corretta è la
seconda, ovvero la condisione tra le capacità continua finchè non si spegne MN1.
Applicando ancora la legge di conservazione della carica:
C1 VOUT,in = C1 VOUT,fin + C2 VZ,in
C1 VDD = C1 VOUT,fin + 0.1C1 (VDD − VTN )
da cui si ottiene:
VOUT,fin = 2.3V
VZ,fin = 2 V
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
16
Esercizio 8
VT0
β′
γ
γ
ΦF
n-channel
p-channel
0.5 V
-0.5 V
100 µA/V
2
50 µA/V 2
0
0.01
V−1
0.6
0
0.01 V−1
0.6
VDD = 2.5 V
Con riferimento al circuito in figura e assumendo VGG =1.5V, SM1 = 8, S M2 = 1 si
risponda ai seguenti quesiti.
1. Individuare la tensione di soglia logica VTL del circuito considerando λ = 0.
Alla soglia logica M1 opera in regione di saturazione. Ipotizziamo che anche il
transistore M2 lavori in saturazione:
ID (M 1) = ID (M 2)
1 ′
1 ′
βn Sn (VGG − VTN )2 =
β Sp (VTL − VDD − VTP )2
2
2 p
VTL = 1.5 V
Il valore ottenuto conferma M2 in saturazione.
A.A. 2006/2007
Corso di Circuiti Elettronici Digitali LA
17
2. Calcolare l’espressione analitica ed il valore numerico dei parametri differenziali
dei transistori nel punto di lavoro precedente assumendo λ = 0.01 V−1 .
gm2 = βn′ Sn (VGG − VTN )(1 + λVTL ) = 101.5µS
gm1 = βp′ Sp (VTL − VDD − VTP )[1 − λ(VTL − VDD )] = 202µS
gd2 = 12 βn′ Sn λ(VGG − VTN )2 = 0.5µS
gd1 = 12 βp′ Sp λ(VTL − VDD − VTP )2 = 0.5µS
3. Disegnare il circuito equivalente ai piccoli segnali e calcolare il guadagno di tensione Av = vout /vin , considerando i parametri differenziali calcolati nel punto
precedente.
Av = −
gm1
∼
= 202
gd1 + gd2
A.A. 2006/2007