lezioni 17-18

Trasp. 173
Correnti alternate
Correnti alternate
Forza elettromotrice del generatore
E  V cost 

2
 2  (rad s 1 )
T

1
T
( s1 )
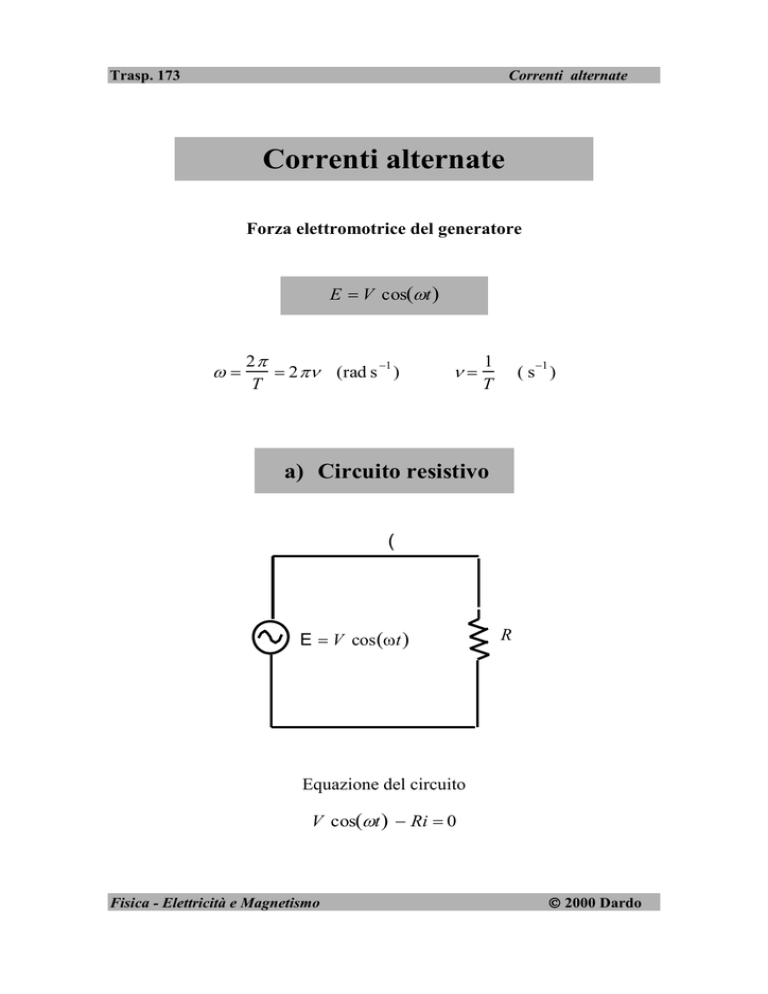
a) Circuito resistivo
(
E  V cos t 
R
Equazione del circuito
V cost   Ri  0
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 174
Correnti alternate
i
V
cost 
R
v R  V cost 
i  I cost 
I
v
V
R
i
vR
i
t
La corrente i e la tensione vR ai capi del resistore sono in fase
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 175
Correnti alternate
b) Circuito capacitivo
E  V cos t 
C
Equazione del circuito
V cost  
q
0
C
q  C V cost 
i
dq
dt

 

i   C V sin t    C V cost  

2 
Reattanza capacitiva ()
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 176
Correnti alternate
XC 
1
C
v C  V cost 
i  I sin t 
I
v
V
XC
i
vC
i
t
La corrente i è sfasata (in anticipo di T/4) rispetto
alla tensione vC ai capi del condensatore
c) Circuito induttivo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 177
Correnti alternate
L
E  V cos t 
Equazione del circuito
V cost   L
di
0
dt
di V
 cost 
dt L

i
di 
V
L
 cost  dt
V
V
 


sin t  
cos

t

L
 L 
2 
Reattanza induttiva ()
XL   L
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 178
Correnti alternate
v L  V cos t 
i  I sin t 
I
v
V
XL
i
vL
i
t
La corrente i è sfasata (in ritardo di T/4) rispetto
alla tensione vL ai capi dell’induttore
Circuito RLC
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 179
Correnti alternate
C
(
R
E  V cos t 
L
Equazione del circuito
L
di
q
 R i   V cos t 
dt
C
d 2i
di 1
L 2  R  i    V sin  t 
dt
dt C
Risoluzione dell’equazione differenziale
e jt  cost   j sin t 
i  I e j t  
Fisica - Elettricità e Magnetismo
j  1
E  V e jt
 2000 Dardo
Trasp. 180
Correnti alternate
di
j t  
 j Ie
dt
d 2i
2
j t  
2   Ie
dt

  2 L I  j  R I  1 I 
 e j   j  V

C 
 1

R
j  V  j

  2  I  j  I 
e
 L C

L
L
R 
V  j
 2
2

   j  I  j  e

0


L 
L
R 
V
 2
2




j

I

j

cos  j sin  


0



L 
L

V
sin    02   2  I
L

V
R
cos    I
L
L
L  20   2
tan  
R

1/ 2
2


1  
2
I  V R   L 
 


C
 

Circuito RLC
E  V cost 
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 181
Correnti alternate
i  I cos t   
I
V
Z
Impedenza del circuito ()
2

1 
Z  R   L 


 C 
2
Reattanza del circuito()
X  L
1
 X L  XC
C
Angolo di fase
tan  

1  1

  L
R  C

Circuito RLC in oscillazione forzata
Corrente in ritardo rispetto alla f.e.m. applicata (<0)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 182
E
Correnti alternate
i
E
i
t
Corrente in anticipo rispetto alla f.e.m. applicata (>0)
E
i
E
i
t
Casi particolari
a) Circuito LC
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 183
Correnti alternate
C
(
E  V cos t 
L
R0
 

2

Z  X  X L  XC
XC  XL 


2
XC  X L 
E  V cost 
 

i  I cost     Isin  t 

2 
XC  XL 
 

i  I cost    I sin t 

2 
XC  XL 
I
V
XL  XC
 L
Fisica - Elettricità e Magnetismo
1
C
 2000 Dardo
Trasp. 184
E
Correnti alternate
i
E
i
t
Corrente i sfasata (in anticipo di T/4) rispetto alla f.e.m. applicata
 L
E
1
C
i
E
i
t
Corrente i sfasata (in ritardo di T/4) rispetto alla f.e.m. applicata
b) Circuito RL
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 185
Correnti alternate
(
R
E  V cos t 
L
C
Z  R2  XL2

tan   
L
R
E  V cost 
i  I cost   
I
  0 
V
Z
Circuito RL
Corrente in ritardo rispetto alla f.e.m. applicata (<0)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 186
E
Correnti alternate
i
E
i
t
c) Circuito RC
C
(
E  V cos t 
L0
Fisica - Elettricità e Magnetismo

R
Z  R 2  XC2
 2000 Dardo
Trasp. 187
Correnti alternate
tan  
1
R C
E  V cost 
i  I cost   
I
  0 
V
Z
Circuito RC
Corrente in anticipo rispetto alla f.e.m. applicata (>0)
E
i
E
i
t
Risonanza
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 188
Correnti alternate
Frequenza angolare
massima
  0 
1
LC

L
1
C

Impedenza minima
ZR

Ampiezza della corrente
massima
V
I
R
Corrente in fase con
la f.e.m. applicata
 0
Circuito RLC in risonanza
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 189
Correnti alternate
E  V cos 0t 
i  I cos 0 t 
I
V
R
0 
1
LC
 1 
E  V cos
t 
 LC 
 1 
i  I cos
t 
 LC 
E
i
i
E
t
Potenza nei circuiti a corrente alternata
Potenza istantanea fornita dal generatore di f.e.m.
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 190
Correnti alternate
p  E i  V I cost  cost   
p  V I cos2 t  cos  V I sin t cost sin 
Potenza media fornita dal generatore di f.e.m.
1
P  p t  
T
1
cos t  
T
2

T
0

T
0
p t  dt
cos 2 t  dt 
1
2
Potenza attiva
P
1
V I cos 
2
Fattore di potenza
cos  
R
Z
Potenza istantanea dissipata nella resistenza
pR  R I 2 cos2 t   
Potenza media dissipata nella resistenza
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 191
Correnti alternate
1
R I2
2
PR  p R t  
P
1
1V
1
V I cos  
R I  RI 2
2
2 Z
2
Potenza attiva = Potenza dissipata in R
P  PR
Condizione di risonanza
  0 
1
LC

ZR

Potenza attiva massima
cos  1
Valori quadratici medi
(Valori efficaci)
Ee 
Fisica - Elettricità e Magnetismo
E2
Ie 
i2
 2000 Dardo
Trasp. 192
Correnti alternate
E
i
2
2

1

T

1
T
T
T
0

0
1
E t  dt 
T
2
i  t  dt 
2
Ee 
V
2
1
T

T
0

V2
V cos t  dt 
2
T
2
0
2
I cos t    dt 
2
Ie 
2
I2
2
I
2
P  Ee Ie cos
P  PR  R Ie2
Trasformatori
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 193
Correnti alternate
i
(
E1  V1 cos t 
L1
L2
N1
N2
V1 cos t   L1
E1e 
di1
0
dt
V1
sin t 
 L1
i1 
E2  M
E2 t 
di1
V
  M 1 cos t 
dt
L1
V1
=
2
=E2e 
M V1
L1 2

E2e M

E1e L1
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 194
Correnti alternate
Flussi concatenati
Primario
Secondario
N1  B 1  L1 i1
N 2  B 2   L2 i2
N 2  B 1  M i2
N1  B  2  M i1

M L2 N2


L1 M N1

E2e N 2

E1e N1
N2
 rapporto di trasformazione
N1
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 195
Onde elettromagnetiche
Equazioni di Maxwell
Legge di Ampère generalizzata
-
-
-
+
+
+
E t 
S1
S2
i t 
flusso del campo elettrico E attraverso la superficie S1:
E  E A
E
q
0 A

E 
Fisica - Elettricità e Magnetismo
q
0
 2000 Dardo
Trasp. 196
Onde elettromagnetiche
0
d E dq

i
dt
dt
Corrente di spostamento (ampère (A))
id   0
d E
dt
Corrente di conduzione (ampère (A))
i
dq
dt
Legge di Ampère generalizzata
CB   0 i   0  0

l
d E
dt
B  dl   0 i   0  0
d E
dt
Campo B indotto da variazioni di E
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 197
Onde elettromagnetiche
(E aumenta al variare di t)
E
B
Campo E indotto da variazioni di B
(B aumenta al variare di t)
B
E
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 198
Onde elettromagnetiche
Equazioni di Maxwell
(forma integrale)
(nel vuoto)
E 
E 
Q
Teorema di Gauss per E
0
d B
dt
Legge di Faraday
B  0
Teorema di Gauss per B
CB   0 i   0  0
d E
dt
Legge di Ampère generalizzata

Q

E  dS 

E  dl  

B  dS  0

B  dl   0 i   0  0
S
l
S
l
Fisica - Elettricità e Magnetismo
0
d
dt
 B  dS
S
d
dt
 E  dS
S
 2000 Dardo