lezioni 5-6

Trasp. 33
Il potenziale elettrico
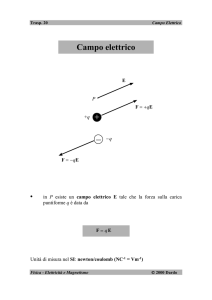
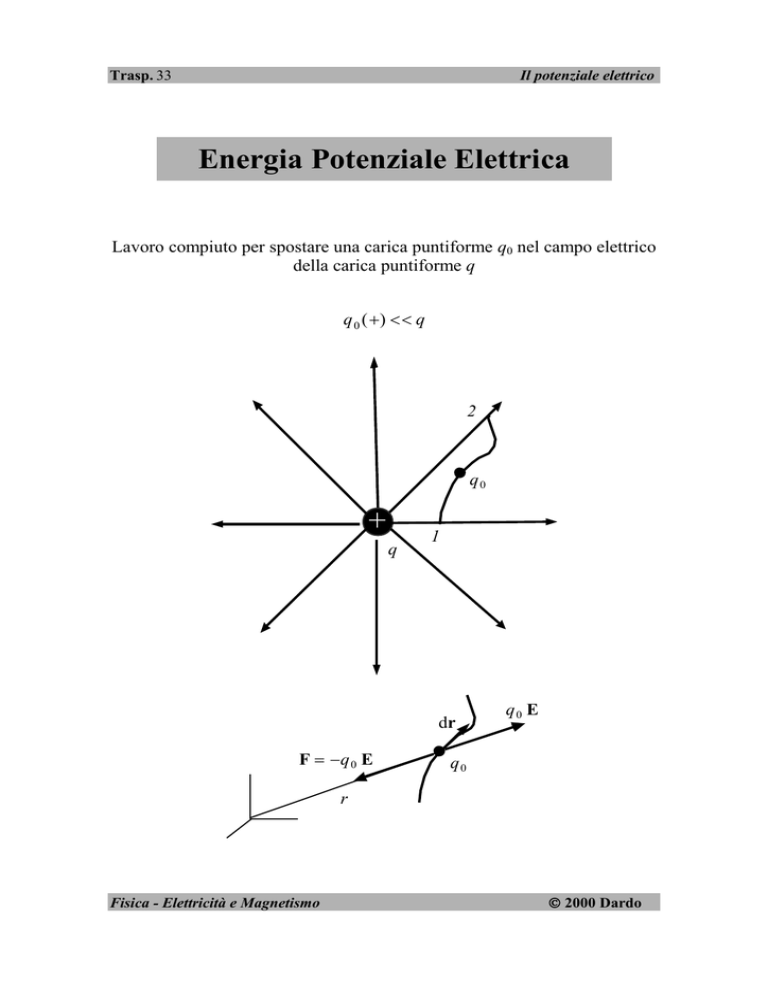
Energia Potenziale Elettrica
Lavoro compiuto per spostare una carica puntiforme q0 nel campo elettrico
della carica puntiforme q
q 0 ()  q
2
.
q0
.
+
q
1
dr
F  q 0 E
q0 E
q0
r
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 34
Il potenziale elettrico
Lavoro compiuto da F
dW  F dr  q0E dr
W12
qq0

4  0

2
1
rˆ  dr
r2
rˆ dr  dr
dr
r+dr
r̂
r
W12
qq0

4  0
W12 

r2
r1
dr
r2
qq0  1 1 
  
4  0  r 2 r1 
Non dipende dal cammino di integrazione
ma solo dagli estremi
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 35
Il potenziale elettrico
W12  U2  U1
U2 = energia potenziale del punto 2
U1 = energia potenziale del punto 1
Unità di misura di U nel sistema SI: joule (J)
Caso generale
U 2  U1  q0
2
 E  dr
1
F
1
.
.
q0
E
2
E
La Forza elettrica è conservativa
W12 non dipende dal cammino di integrazione
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 36
Il potenziale elettrico
(percorso della carica q0 nel campo
generato dalla carica q)
Se il punto P1 coincide con P2 (percorso chiuso)
W12  U2  U1  0

W12  l F dr 0

C(F)  l F dr 0

Circuitazione di F = 0  Forza elettrica conservativa
Il Campo elettrico è conservativo

l F dr   q 0 l E dr  0

Circuitazione di E = 0  Campo elettrico conservativo
Potenziale Elettrico
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 37
Il potenziale elettrico
Energia potenziale per unità di carica

U
q0
Unità di misura nel sistema SI: volt=joule/coulomb (V = J C-1)
Differenza di potenziale elettrico
2  1 
W12 U2  U1

q0
q0
Carica puntiforme
Differenza di potenziale
2  1 
q  1 1 
  
4  0  r2 r1 
1  0
r1  

Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 38
Il potenziale elettrico
Potenziale di una carica puntiforme

1
q
4  0 r
Potenziale di una distribuzione discreta di cariche

1
4  0
qi
r
i
i
Potenziale di una distribuzione continua di carica

1
4  0

dq
r
(dq   dV; dq   dS; dq   dl)
Superficie equipotenziale
Luogo dei punti per cui  = costante
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 39
Il potenziale elettrico
Carica puntiforme
E
Superfici
equipotenziali
+
Campo elettrico uniforme
E
Superfici equipotenziali
Esempi
Campo elettrico uniforme
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 40
Il potenziale elettrico
.
1
F
2
.
E
q0
q0 E
dr
d
x1
x2
x
E dr  E cos dr  E dx

2
 2   1   E  dr  E
1

x2
x1
dx  E  x2  x1 
V  2  1  E d
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 41
Condensatori
Capacità elettrica
Esempio: sfera conduttrice con carica Q
+
+
   0  cost
+
.P
+
+
r
S
+
+
+
+
+
+
+
All’interno della sfera e sulla superficie:
  0 
1 Q
4  e0 R
(R = raggio della sfera)

Q  4   0 R 0

Q  C 0
C = capacità del conduttore
Unita di misura nel SI: farad = coulomb/volt (F = CV-1)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 42
Condensatori
Esempio: Sfera Conduttrice
Carica Q distribuita uniformemente sulla superficie della sfera
(R = raggio della sfera)
Er  
 r  
1
Q
4  0 r 2
(r  R)
1
Q
40 r
  R 
C
(r  R)
1
Q
4  0 R
Q
 4 0 R
  R
Esempio: R = 1 m
C  4 0 
1
1
10

F = 0.1 nF
9  10
k 0 9  10
Farad  F =
Fisica - Elettricità e Magnetismo
C
C
C2
 1 
V JC
Nm
 2000 Dardo
Trasp. 43
Condensatori
Condensatore
sistema di due conduttori
Esempio: condensatore piano
+Q
+ + + ++ + ++ +++
2
E
d
1 - - - - - - - - - - -Q
V  2  1
E

Q

 0 A 0
V  Ed  Q
C
0 A
Q
V
C  0
Fisica - Elettricità e Magnetismo
d
A
d
 2000 Dardo
Trasp. 44
Condensatori
Condensatori in serie e in parallelo
Simbolo di condensatore
1.
Condensatori in serie
V2
V1
V3
C2
C1
-Q
+Q
C3
+Q -Q
-Q
+Q
V
V1 
Q
C1
Q
C2
V2 
V3 
Q
C3
 1
1
1 
V  V1  V 2  V3  Q  
 
C1 C2 C3 
Q
C
V

N condensatori in serie:
1
1
1
1



C C1 C2 C3
1

C
1.
1
C
i
i
Condensatori in parallelo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 45
Condensatori
Q1
C1
Q2
C2
Q3
C3
V
Q1  C1V
Q2  C2V
Q3  C3V
Q  Q1  Q2  Q3  C1  C2  C3 V
Q
V
C

C  C1  C 2  C3
N condensatori in parallelo:
C
C
i
i
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 46
Dielettrici
Dielettrici
• Omogenei
DIELETTRICI
• Isotropi
• Lineari
1. Q non varia
+Q + + + + + + + + + + +
V0
-Q
- - - - - - - - - - -
+Q + + + + + + + + + + +
V  V0
-Q
- - - - - - - - - - -
V
C
V0
r
r  1
Q
Q
Q

 r
  r C0
V V 0 / r
V0
2. V0 non varia
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 47
Dielettrici
+Q + + + + + + + + + + +
V0
-Q
- - - - - - - - - - -
+Q' + + + + + + + + + + +
V0
-Q'
- - - - - - - - - - -
Q'  Q
C
Q'   rQ
Q'  r Q

  r C0
V0
V0
C  C0
C   r C0
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 48
Dielettrici
Suscettività elettrica
e   r  1
Valori di capacità (F)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 49
Dielettrici
10-4 F
5 10-5
10-5
10-9
8 10-11
- Condensatore per motore elettrico
- Condensatore per illuminazione auto
- Condensatore per flash elettronico (potenza 106 W)
- Condensatore ad aria per la ricezione di onde radio
- 1 m di cavo coassiale per la televisione
Valori della costante dielettrica relativa
- Titanato di bario
- Biossiodo di titanio
- Acqua (25 C)
- Porcellana
- Teflon
- Aria (760 mm Hg, 0 C)
- Vuoto (definizione)
5000
100
78
10
2
1.00059
1
Rigidità dielettrica (105 Vm-1)
(Campo elettrico massimo sopportato dal dielettrico)
- Teflon
- Vetro
- Carta
- Titanato di bario
- Aria
800
500
150
40
30
Polarizzazione del dielettrico
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 50
Dielettrici
+Q + + + + + + + + + + +
E0
-Q
V0
- - - - - - - - - - -
- - - - - - - - - - E1
+ + + ++ + ++ +++
E1
V
+ + + + + + + + + ++ - - - - - - - - - - -
E0 = campo presente in assenza di dielettrico
E1 = campo prodotto dalle densità di cariche indotte sulle superfici del
dielettrico (cariche di polarizzazione)
E = campo risultante
E  E0  E1

E  E0
V  V0
Fisica - Elettricità e Magnetismo
 2000 Dardo