lezioni 15-16

Trasp. 143
Proprietà magnetiche della materia
Proprietà Magnetiche della Materia
• Omogenei
MATERIALI
• Isotropi
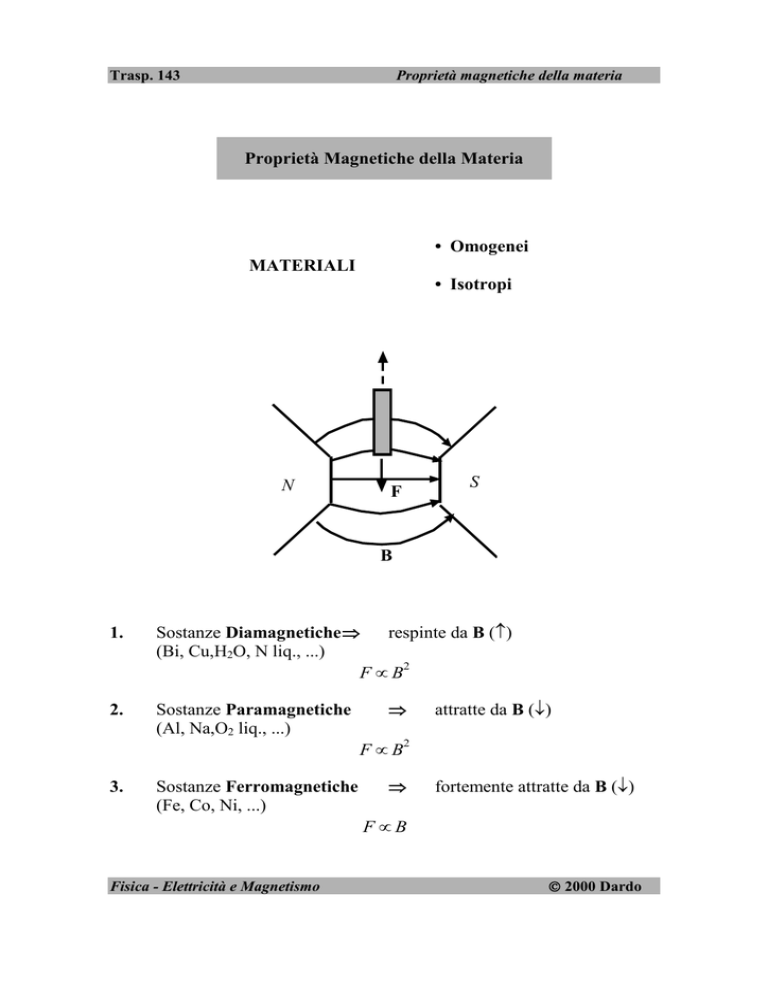
N
F
S
B
1.
Sostanze Diamagnetiche 
respinte da B ()
(Bi, Cu,H2O, N liq., ...)
F  B2
2.
Sostanze Paramagnetiche
(Al, Na,O2 liq., ...)
3.
Sostanze Ferromagnetiche
(Fe, Co, Ni, ...)

attratte da B ()
F  B2

fortemente attratte da B ()
FB
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 144
Proprietà magnetiche della materia
I
1.
B0
B
L0
L   r L0
Sostanze Diamagnetiche
L  L0
2.
 r  1 (cost)
Sostanze Paramagnetiche
L  L0
3.
I
 r  1 (cost)
Sostanze Ferromagnetiche
L  L0
 
 r  1 (dipende da i)
 = permeabilità magnetica
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 145
Proprietà magnetiche della materia
 
 
0 = permeabilità magnetica del vuoto
r = permeabiltà magnetica relativa
  r 0
r  1   m
 m  suscettività magnetica
m
Materiale
Diamagnetico
- 9.1 10-6
- 9.6 10-6
Acqua
Rame
Paramagnetico
7.2 10-6
2.2 10-5
Sodio
Alluminio
Ferromagnetico
5.5 103
105
Ferro
Mu-metal
B  B0  B1
B1 = campo magnetico indotto nel materiale da B0
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 146
Proprietà magnetiche della materia
Diamagnetismo
B 0 B1
B0
B0

momenti di dipoli magnetici atomici indotti

campo magnetico B1 opposto a B0
B  B0

 0
r 1
m  0
Paramagnetismo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 147
Proprietà magnetiche della materia
B 0 B1
B0
B0

allineamento dei momenti di dipoli magnetici atomici permanenti

campo magnetico B1 stesso verso di B0
B  B0

 0
r 1
m  0
Ferromagnetismo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 148
Proprietà magnetiche della materia
B 0 B1
B0
Curva di magnetizzazione
B1
B1max
B0
Ciclo di isteresi
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 149
Proprietà magnetiche della materia
B
B0
Domini magnetici
B0  0
Fisica - Elettricità e Magnetismo
B0
 2000 Dardo
Trasp. 150
Circuiti con correnti variabili
Circuiti con correnti lentamente
variabili
Correnti lentamente variabili (quasi stazionarie)
(Campi elettrici e magnetici lentamente variabili)
 
2 c
l
(l = dimensioni lineri del circuito)
(rad s-1)
 = 2  c/ (m)
linea elettrica
314 (50 Hz)
6 106
onde radio
5 106
300




Analisi dei circuiti

Estensione dei principi di Kirchhoff
con l’inclusione delle forze elettromotrici indotte
Regime transitorio
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 151
2.
Circuiti con correnti variabili
Circuito RC
a) Carica di un condensatore
i
C
E(
R
t 0 
 q0
inserimento di E
Equazione del circuito
E 
E 
q
 Ri
C
q
dq
R
C
dt
dq E C  q

dt
RC

q
0
dq
1

EC q
RC
Fisica - Elettricità e Magnetismo
t
 dt
0
 2000 Dardo
Trasp. 152
Circuiti con correnti variabili
ln E C  q   
t
RC


q t   Q 1  e t/ 
C

 C  RC
Q EC
(C = costante di tempo capacitiva del circuito (s))
(t = 5C

q = 0.993Q)
q
Q
t
Intensità di corrente
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 153
Circuiti con correnti variabili
t
dq E  
i
 e
dt R
C

i I e
I

t
C
E
R
i
I
t
(t = 5C

q = 0.006I)
b) Scarica di un condensatore
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 154
Circuiti con correnti variabili
i
C
R
t=

q =Q
Equazione del circuito


q
 Ri
C
q
dq
R
C
dt
dq
q

dt
RC

q
Q
Fisica - Elettricità e Magnetismo
dq
1

q
RC

t
0
dt
 2000 Dardo
Trasp. 155
Circuiti con correnti variabili
ln
q
t

Q
RC

q Qe

t
C
q
Q
t
(t = 5C

q = 0.006Q)
Intensità di corrente
t
dq
Q 
i

e
dt
RC
Fisica - Elettricità e Magnetismo
C
 2000 Dardo
Trasp. 156
Circuiti con correnti variabili

i  I e
I
V
R

t
C
V
Q
C
i
t
-I
Energia nel circuito RC
Energia dissipata nella resistenza R
durante la scarica del condensatore
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 157
Circuiti con correnti variabili
U

U


0
2
RI e
0


2
Ri dt
2
t
RC
dt 
1
CV2
2

Energia accumulata nel campo E del condensatore
Energia fornita dal generatore
durante la carica del condensatore
U
E2
U
R

Q

0
0
 E dq   E i dt
 
0
e
t
C
dt  C E 2  C V 2

1
CV 2
2
1
CV2
2
1.

accumulata nel condensatore

dissipata nella resistenza
Circuito RL
a) Crescita della corrente
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 158
Circuiti con correnti variabili
i
L
E(
R
t 0 
inserimento di E
 i0
Equazione del circuito
E  L
di
 Ri
dt
di E  Ri

dt
L

i
0
di
1

E  Ri
L
t
 dt
0
1
t
ln E  Ri   
R
L

(extracorrete di chiusura)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 159
Circuiti con correnti variabili

i t   I 1  e t/ 
I
E
R
L
L 

L
R
(L = costante di tempo induttiva del circuito (s))
(t = 5L

i = 0.993I)
i
I
t
b) Decadimento della corrente
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 160
Circuiti con correnti variabili
i
L
R

t=0
i=I
Equazione del circuito
L
di
 Ri
dt
di E  Ri

dt
L
di
Ri

dt
L

i
I
Fisica - Elettricità e Magnetismo
di
R

i
L
t
 dt
0
 2000 Dardo
Trasp. 161
Circuiti con correnti variabili

(extracorrete di apertura)
i t   I e t / 
L
i
I
t
(t = 5L

i = 0.006I)
Energia nel circuito RL
Energia dissipata nella resistenza R durante la diminuzione di i
U
Fisica - Elettricità e Magnetismo


0
2
Ri dt
 2000 Dardo
Trasp. 162
Circuiti con correnti variabili
U


0
2
RI e

2R
t
L
dt 
1 2
LI
2

Energia accumulata nel campo B dell’induttanza
Energia fornita dalla pila dopo la chiusura del circuito
E i dt  Ri 2 dt  Li di
Potenza fornita dalla pila
di
E i  Ri 2  L i
dt
E2
R
Ei
R i2
Li
di
dt
t
Circuiti RLC
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 163
Circuiti con correnti variabili
C
(
i
R
E
L
t 0
 q0
i 0
Equazione del circuito
L
di
q
 Ri   E
dt
C

L
d 2i
di
1

i0
2  R
dt
dt
C
 
Fisica - Elettricità e Magnetismo
R
2L
 20 
1
LC
 2000 Dardo
Trasp. 164
Circuiti con correnti variabili
d 2i
di
2
 0 i  0
2  2
dt
dt
i  e t

i  C1e a t  C2 e a t
1
2
1,2      2   20
1.
Sovrasmorzamento
 2   20

R2 

e t
1
e  t  esponenziali
2
4L
C
decrescenti
i
t
2.
Smorzamento crictico
 2   02


R2 
4L
C
andamento della corrente come nel caso precedente
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 165
3.
Circuiti con correnti variabili
Sottosmorzamento
 2   20
i 

R2 
4L
C
E t
e sin t
L
   20   2 =
i
t

1
R2

LC 4 L2
(frequenza naturale del circuito)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 166
Circuiti con correnti variabili
Circuito oscillante
R0

 0
(smorzamento nullo)
+Q
C
V
E max
-Q
t 0
L
 qQ
vV
i 0
Equazione del circuito
L
di q
 0
dt C
d2 q
q

0
dt 2 L C
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 167
Circuiti con correnti variabili
d2 q
2
2  0 q  0
dt

(Equazione differenziale tipo quella del moto armonico)

Integrale generale
q  A cos 0t   
Carica sulle armature del condensatore
q  Q cos 0t 
Differenza di potenziale tra le armature del condensatore
v  V cos 0t 
V
Fisica - Elettricità e Magnetismo
Q
C
 2000 Dardo
Trasp. 168
Circuiti con correnti variabili
i
dq
dt

Intensità di corrente
i  I sin  0t 
I   0 Q
Frequenza caratteristica
0 
1
LC
Andamento della carica q e della corrente i in funzione del tempo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 169
Circuiti con correnti variabili
q
Q
t
i
I
t
Energia accumulata nel campo elettrico E del condensatore
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 170
Circuiti con correnti variabili
1
1 Q2
2
2
UE  C v 
cos  0 t 
2
2 C
Energia accumulata nel campo magnetico B dell’induttore
UB 
1
1
1 Q2
2
2
2
2
2
L i  L  0 Q sin  0 t  
sin  0 t 
2
2
2 C
1 Q2 1
2
U  UE  UB 
 CV
2 C 2
UE
UB
U
t
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 171
Circuiti con correnti variabili
+Q
C
V
-Q
E
L
t=0
max
I
B
max
t=T/4
(
-Q
t=T/2
-V
E
max
+Q
Fisica - Elettricità e Magnetismo
 2000 Dardo