lezioni 13-14

Trasp. 119
Induzione elettromagnetica
Induzione elettromagnetica
Base sperimentale
(Esperimenti di Faraday - 1831)
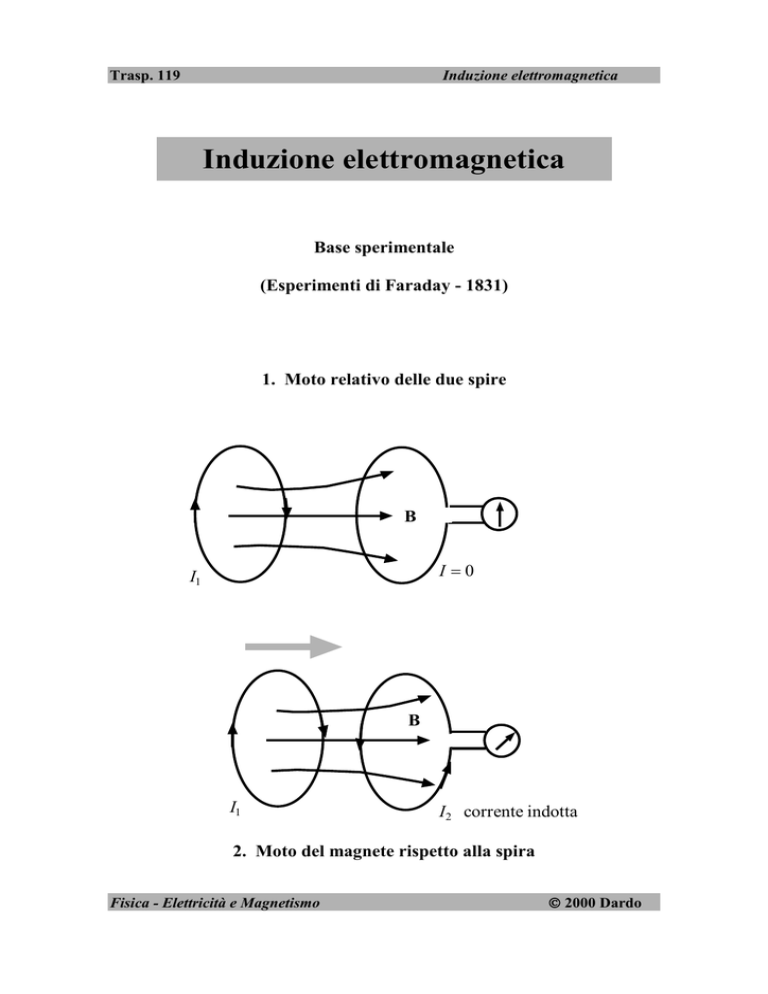
1. Moto relativo delle due spire
B
I0
I1
B
I1
I2 corrente indotta
2. Moto del magnete rispetto alla spira
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 120
Induzione elettromagnetica
B
S
N
I corrente indotta
3. Mutua induzione
t0 I0
t  0 I  I1
t  0 I  I1
B
t0
I0
t0
I  I2
t0
I0
corrente indotta
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 121
Induzione elettromagnetica
Legge di Faraday dell’induzione elettromagnetica
Variazione di B nel tempo

forza elettromotrice indotta nella spira
B
I
S
E
Legge di Faraday
E=

d B
dt
E = forza elettromotrice indotta nella spira (volt)
B = flusso del campo magnetico attraverso una superficie di cui la spira
è contorno (weber)
Osservazioni
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 122
1.
Induzione elettromagnetica
Il flusso B può variare in seguito ad una variazione:
a) del campo magnetico;
b) della superficie attraverso cui si calcola B.
2.
Flusso tagliato:
a)
il circuito si muove o si deforma in una regione delle spazio dove
esiste B;
b)
la sorgente di B si muove rispetto al circuito.
3.
Flusso concatenato:
Circuito sorgente di B (primario) e circuito secondario fissi
variazione di corrente nel primario

variazione di B

variazione di B
Il campo elettrico indotto non è conservativo
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 123
Induzione elettromagnetica
E = fem indotta (non localizzata)

Lavoro per unità di carica (volt) necessario
per portare una carica lungo un percorso chiuso

E=
  E  dl
l

Legge di Faraday


l
E  dl  
d B
dt

E = campo elettrico indotto non conservativo

In ogni regione dello spazio dove il
campo magnetico B varia nel tempo
è presente un campo elettrico E non conservativo
Intensità della corrente indotta
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 124
Induzione elettromagnetica
(R = resistenza della spira)
i
E
R

i 
1 d B
R dt
Bobina formata da N spire in serie
B
I
E=
N
d B
dt
Segno della fem e verso della corrente indotta
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 125
Induzione elettromagnetica
B
B
I
I
B  0
d B
0
dt
E 0
B  0
E 0
I
I
B
B  0
d B
0
dt
B
d B
0
dt
E 0
B  0
d B
0
dt
E 0
Legge di Lenz
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 126
Induzione elettromagnetica
La corrente indotta genera, a sua volta, un campo
magnetico che si oppone alla variazione di flusso
che l’ha prodotta.
B inducente (crescente)
I
E
B indotto
B  0
d B
0
dt
E 0
Il segno (-) nella legge di Faraday esprime la legge di Lenz
Applicazioni
1.
Spira ruotante in un campo magnetico uniforme
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 127
Induzione elettromagnetica
A = area della spira
 = velocità angolare = costante
 B  A B cos  A B cos t 
E=

2.
d B
 A B  sin  t 
dt
Generatore di corrente alternata
Bobina con N spire ruotante in un campo magnetico uniforme
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 128
Induzione elettromagnetica
fem alternata

E=
 N
d B
 N A B  sin  t 
dt
i
R
E(
corrente alternata

i
E NAB

sin  t 
R
R
E t   E0 sin  t 
i t   I sin  t 
Fisica - Elettricità e Magnetismo
V
E0  N A B 
I
E0
R
 A
 2000 Dardo
Trasp. 129
Induzione elettromagnetica
Potenza erogata dal generatore

pt   E i  E0 I sin 2  t 
Forza elettromotrice (V)
E
E0
t
Intensità di corrente (A)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 130
Induzione elettromagnetica
i
I
t
Potenza erogata (W)
p
E0 I
t
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 131
Induzione elettromagnetica
Autoinduzione
Coefficiente di autoinduzione
i  B
Flusso attraverso il circuito del campo B
creato dalla corrente i che circola nel circuito stesso
B 
iB
 B  dS
S
(legge di Biot  Savart)

B  i
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 132
Induzione elettromagnetica
B  L i
L = coefficiente di autoinduzione (induttanza) del circuito
Unità di misura di nel sistema SI: henry (H = T m2 A-1 = V s A-1)
Forza elettromotrice di autoinduzione
E=

d B
dt

E=
 L
di
dt
Osservazioni
1.
L costante nel tempo (circuiti fermi e in deformabili);
2.
E = forza controelettromotrice:
di
0
dt

E  0 <<
di
0
dt

E  0 <<
Mutua Induzione
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 133
Induzione elettromagnetica
Campo magnetico generato dalla spira 1 concatenato alla spira 2
I1
B
1
2
Campo magnetico generato dalla spira 2 concatenato alla spira 1
I2
B
1
2
Circuiti accoppiati magneticamente
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 134
Induzione elettromagnetica
Flussi concatenati
(B(1) con la spira 1, B(2) con la spira 2)
 B 1  L1i1  M12i2
 B 2   L2i2  M21i1
Coefficienti di mutua induzione
M12  M21  M
Unità di misura: henry (H)
Forze elettromotrici indotte
(E1 con la spira 1, E2 con la spira 2)
di1
di
M 2
dt
dt
di
di
E2 1 = M 1  L2 2
dt
dt
E1 1 =
 L1
Applicazioni
1.
Coefficiente di autoinduzione di un solenoide (l >> R)
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 135
Induzione elettromagnetica
i
B (uniforme)
A R
2
Flusso attraverso A
 B   R2 B
B  0 n i

 B   0  R2 n i
Flusso concatenato con il solenoide
N  B   0  R2 n N i   0  R 2 n 2 l i
L
N B
i

Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 136
Induzione elettromagnetica
L   0 n 2 R2 l
2.
Coefficiente di autoinduzione di un cavo coassiale (lunghezza l)
B
R1
R2
Campo magnetico tra i due conduttori:
B
Fisica - Elettricità e Magnetismo
0 i
2 r
 2000 Dardo
Trasp. 137
Induzione elettromagnetica
d B  B l dr 
B 
0
il
2

R2
R1
 0 dr
il
2
r
dr  0
R

i l ln 2
r 2
R1
Coefficiente di autoinduzione (H)
L
0
R
l ln 2
2
R1
Coefficiente di autoinduzione per unità di lunghezza (H m-1)
Ll 
Fisica - Elettricità e Magnetismo
 0 R2
ln
2
R1
 2000 Dardo
Trasp. 138
3.
Induzione elettromagnetica
Coefficiente di mutua induzione di una spira e di un solenoide
l
i1
R1
R2
(superficie della spira perpendicolare all’asse del solenoide)
Campo magnetico nel solenoide
B   0 n1 i1
flusso di B attraverso la spira
 B  B  R22   0  R22 n1 i1
M
Fisica - Elettricità e Magnetismo
B
i1
 2000 Dardo
Trasp. 139
Induzione elettromagnetica
M   0  R22 n1
Induttori collegati in serie e in parallelo
Simbolo di induttanza
Fisica - Elettricità e Magnetismo
 2000 Dardo
Trasp. 140
Induzione elettromagnetica
Induttori in serie
(senza accoppiamento magnetico)
i
L1
 L1
L3
L2
di
di
di
di
 L2  L3  L
dt
dt
dt
dt
L  L1  L2  L3
N induttori collegati in serie (non accoppiati magneticamente):
L
L
i
i
Induttori in parallelo
(senza accoppiamento magnetico)
E
Fisica - Elettricità e Magnetismo
L1
L2
L3
 2000 Dardo
Trasp. 141
Induzione elettromagnetica
i  i1  i2  i3
di di1 di2 di3



dt dt dt
dt

E
E E E
 

L
L1 L2 L3
1 1
1
1



=
L L1 L2 L3
N induttori collegati in parallelo (non accoppiati magneticamente):
1

L
1
L
i
i
Energia del campo magnetico
energia magnetica di una corrente
dW  E dq  L
Fisica - Elettricità e Magnetismo
di
dq  L i di
dt
 2000 Dardo
Trasp. 142
Induzione elettromagnetica
U

I
0
L i di 
U
1
L I2
2
1 2
LI
2
Esempio: solenoide(lunghezza l)
L   0 n 2 R2 l
U
1
20
B  0 n I
B2  R2 l 
Densità di energia magnetica (J m-3)
uB 
Fisica - Elettricità e Magnetismo
1
20
B2
 2000 Dardo