DEFINIZIONE DI ASINTOTO
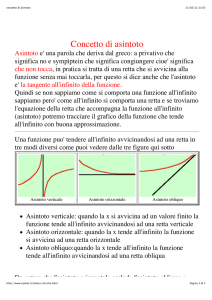
Un asintoto è una retta alla quale la funzione “tende”.
Essendo una retta può essere di tre tipi:
VERTICALE (retta parallela all’asse delle y) di equazione x=k
ORIZZONTALE (retta parallela all’asse delle x) di equazione y=k
OBLIQUO (retta non parallela agli assi) di equazione y= mx+q
ASINTOTO VERTICALE
Si dice che la funzione y=f(x) ha per asintoto verticale la retta x=K se nel punto K
escluso dal dominio, il limite destro e/o il limite sinistro tendono ad infinito.
e/o
Una funzione razionale fratta ha sicuramente un asintoto verticale in un punto escluso
dal dominio, purchè in tale punto il limite tenda ad infinito.
Esempio
y=
D: x
1
e
Pertanto la funzione ha per asintoto verticale la retta x=1.
ASINTOTO ORIZZONTALE
Si dice che la funzione y=f(x) ha per asintoto orizzontale la retta y=K se il limite, per
x che tende a infinito della funzione, tende a K .
o
Una funzione razionale fratta ha sicuramente un asintoto orizzontale se il grado del
numeratore è minore o uguale al grado del denominatore.
Esempio
y=
D: x
1
e
Pertanto la funzione ha per asintoto orizzontale la retta di equazione y=1.
ASINTOTO OBLIQUO
Condizione necessaria affinchè una funzione abbia un asintoto obliquo è che
ovvero che non abbia un asintoto orizzontale.
In tal caso occorre calcolare i valori m e q per poter scrivere l’equazione della retta
y=mx+q.
m=
q=
Tali limiti devono essere finiti e m≠0
Una funzione razionale fratta ha sicuramente un asintoto obliquo se il grado del
numeratore supera di 1 il grado del denominatore.
Esempio
y=
(condizione necessaria soddisfatta)
Calcolo adesso m e q:
m=
q=
1
=
=1
Pertanto l’equazione dell’asintoto obliquo è: y=x+1