x-3

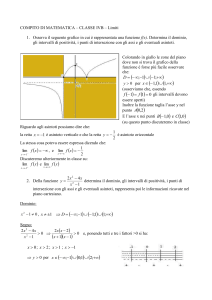
Definizione:
Un asintoto è una retta tangente la curva all’infinito
Verticale
orizzontale
obliquo
ASINTOTI VERTICALI
Essendo una retta verticale e parallela
all’asse delle y (ordinate) la sua equazione
è sempre del tipo «x= K» con K numero reale
RICORDA che nelle funzioni fratte gli asintoti
verticali sono tutti i punti esclusi dal campo di esistenza
Esempio y=2x
x-1 il dominio R-{1} tutto R escluso 1; x≠1
Asintoto verticale x=1
Lim f(x) = - ∞
x->1-
Lim f(x) = + ∞
x->1+
Esempio di studio di funzione con asintoto verticale
Y= 2x
x-2
X=2
È asintoto verticale
1. Funzione razionale fratta di grado 2
2. Dominio x-2≠0 x ≠2 (-∞;2)U(2; ∞)
3. Simmetrie f(-x)= 2(-x)/(-x)-2 = - 2(x)/-x-2 f(x) ne pari ne dispari
4. Intersezioni con assi
y=f(x)
y=f(x) O(0,0)
x=0
y=0
5. Studio del segno 2x >0 N. >0 2x>0
x>0
0
2
x-2
D.>0
x-2>0 x>2
+
- +
Asintoti verticali
x=2
NO
Lim f(x) = - ∞
lim f(x) = + ∞
x->2x->2+
Asintoti orizzontali
Si ha un asintoto orizzontale (retta parallela asse x quindi di equazione y=l)
quando, al crescere della x la y si avvicina ad un valore ben determinato.
C'e' l'asintoto se
Lim f(x)= l con l numero finito
x->∞
Esempio y= x-3
x2-9
Ricerco gli asintoti orizzontali: calcolo se esiste il limite……
Lim x-3 = ∞ questa è una forma indeterminata
x->∞ x2-9
∞
per eliminare l’indeterminazione procedo ricordando che x2-9=(x-3)(x+3)
Lim
x-3
= 1 =0
x->∞ (x-3)(x+3)
∞
Ho trovato che il limite è uguale ad un numero finito “0” quindi l’asintoto orizzontale
è y=0 che coincide con l’equazione dell’asse delle x