Circuiti con due generatori di tensione – esercizio n. 1
metodo dei potenziali di nodo
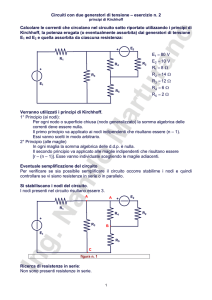
Calcolare le correnti che circolano nel circuito sotto riportato utilizzando il metodo
dei potenziali di nodo, la potenza erogata (o eventualmente assorbita) dai generatori
di tensione E1 ed E2 e quella assorbita da ciascuna resistenza:
+
E1
E1 = 40 V
R1
E2 = 10 V
R4
R1 = 8 Ω
R3
R2 = 4 Ω
R3 = 40 Ω
R 4 = 10 Ω
R5
R2
R5 = 8 Ω
E2
+
Verrà utilizzato il metodo dei potenziali di nodo che sfrutta il 1° principio di Kirchhoff.
1° Principio (ai nodi):
Per ogni nodo o superficie chiusa (nodo generalizzato) la somma algebrica delle
correnti deve essere nulla.
Il primo principio va applicato ai nodi indipendenti che risultano essere (n – 1).
Essi vanno scelti in modo arbitrario.
Eventuale semplificazione del circuito
Per verificare se sia possibile semplificare il circuito occorre stabilirne i nodi e quindi
controllare se vi siano resistenze in serie o in parallelo.
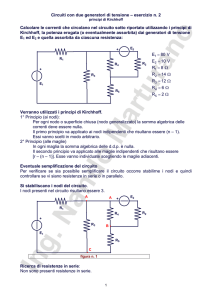
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano essere 2.
A
+
E1
R4
R1
R3
B
B
R2
A
R5
E2
+
A
figura n. 1
1
Circuiti con due generatori di tensione – esercizio n. 1
metodo dei potenziali di nodo
Ricerca di resistenze in serie:
Non sono presenti resistenze in serie.
Ricerca di resistenze in parallelo:
Le resistenze R3, R4, R5 risultano essere in parallelo perché ciascuna di esse è compresa
fra gli stessi nodi A e B.
Calcolo della resistenza equivalente;
1
1
R AB =
=
=4Ω
1
1
1
1
1 1
+
+
+
+
R3 R 4 R5 40 10 8
Disegno del circuito:
Si disegna un nuovo circuito in cui vengono sostituite le tre resistenze R3, R4 R5 con la sola
resistenza RAB.
+
A
E2
E1
+
R1
RAB
R2
B
figura n. 2
Tale circuito non può essere ulteriormente semplificato
Si stabiliscano i nodi, i nodi indipendenti ed i rami del circuito.
In tale circuito si individuano n = 2 nodi, (n – 1) = (2 – 1) = 1 nodo indipendente ed r = 3
rami.
Si disegnino, come in figura 3, in modo arbitrario, le correnti di ramo che risulteranno
essere 3, perchè tanti sono i rami.
+
A
E1
E2
IAB
R1
+
RAB
I1
I2
R2
B
figura n. 3
Si fissi il potenziale di riferimento per un nodo scegliendolo in modo arbitrario: VB = 0
Si proceda nella scrittura di tutte le d.d.p. presenti ai capi di ciascun ramo tra i nodi del
circuito tenendo conto che VB = 0 e si ricavino le rispettive correnti:
2
Circuiti con due generatori di tensione – esercizio n. 1
metodo dei potenziali di nodo
AB ⎧ VA = E1 − R1 ⋅ I1
⎪
AB ⎨ VA = R AB ⋅ IAB
AB ⎪⎩ VA = −E2 + R2 ⋅ I2
⎧
E1 − VA
= G1 ⋅ (E1 − VA )
⎪I1 =
R
1
⎪
VA
⎪⎪
= GAB ⋅ VA
⎨IAB =
R
AB
⎪
⎪
V + E2
= G2 ⋅ ( VA + E2 )
⎪I2 = A
R2
⎪⎩
Si applichi il primo principio di Kirchhoff all’unico nodo indipendente A:
•A
I1 = I2 + IAB
Sostituendo i valori delle correnti ricavate in precedenza si ottiene:
G1 ⋅ (E1 − VA ) = G2 ⋅ ( VA + E2 ) + GAB ⋅ VA
Semplificando:
G ⋅ E − G2 ⋅ E 2
VA = 1 1
G1 + G2 + GAB
Tale formula, particolarmente semplice da ricordare e da scrivere, è valida solo nel caso di
circuiti a due nodi; essa prende il nome di Teorema di Millman. Tale teorema costituisce
un caso particolare (2 nodi) del metodo dei potenziali di nodo.
Sostituendo i valori noti:
1
1
⋅ 40 − ⋅ 10
4
=4V
VA = 8
1 1 1
+ +
8 4 4
E quindi le tre correnti richieste:
E − VA 40 − 4
I1 = 1
=
= 4,5A
R1
8
IAB =
I2 =
VA
4
= = 1,0 A
R AB 4
VA + E2 4 + 10
=
= 3,5 A
R2
4
Calcolo delle correnti I3, I4 ed I5:
Per determinare tali correnti, circolanti rispettivamente nelle resistenze R3, R4 ed R5, in
parallelo tra loro perché fra i nodi A e B, occorre determinare la d.d.p. VAB.
VAB = R AB ⋅ IAB = 4 ⋅ 1,00 = 4,00 V
I3 =
VAB 4,00
=
= 0,10 A
R3
40
I4 =
VAB 4,00
=
= 0,40 A
R4
10
I5 =
VAB 4,00
=
= 0,50 A
R5
8
In conclusione le correnti nel circuito risultano essere quelle riportate in figura n. 4:
3
Circuiti con due generatori di tensione – esercizio n. 1
metodo dei potenziali di nodo
A
+
E1
I4
I1
R1
I1 = 4,50 A
R4
I2 = 3,50 A
R3
B
B
R2
I5
I2
A
R5
I3 = 0,10 A
I4 = 0,40 A
I3
I5 = 0,50 A
E2
A
+
figura n. 4
Calcolo della potenza erogata dai generatori:
Poiché in entrambi i generatori il verso della corrente ed il verso positivo della d.d.p.
concordano, allora entrambi erogano potenza.
PE1 = E1 ⋅ I1 = 40 ⋅ 4,50 = 180,00 W
PE2 = E2 ⋅ I2 = 10 ⋅ 3,50 = 35,00 W
PET = PE1 + PE2 = 180,00 + 35,00 = 215,00 W
Calcolo delle potenze assorbite dalle resistenze;
PR1 = R1 ⋅ I12 = 8 ⋅ 4,502 = 162,00 W
PR2 = R2 ⋅ I2 2 = 4 ⋅ 3,502 = 49,00 W
PR3 = R3 ⋅ I3 2 = 40 ⋅ 0,102 = 0,40 W
PR4 = R 4 ⋅ I4 2 = 10 ⋅ 0,402 = 1,60 W
PR5 = R5 ⋅ I5 2 = 8 ⋅ 0,502 = 2,00 W
PRT = PR1 + PR2 + PR3 + PR4 + PR5 = 162,00 + 49,00 + 0,40 + 1,60 + 2,00 = 215,00 W
NB: Si noti come la somma algebrica delle potenze erogate o assorbite dai generatori è
pari alla somma delle potenze dissipate su ciascuna resistenza presente nel circuito.
4