Formulario geometria analitica da studiare
2C/2E
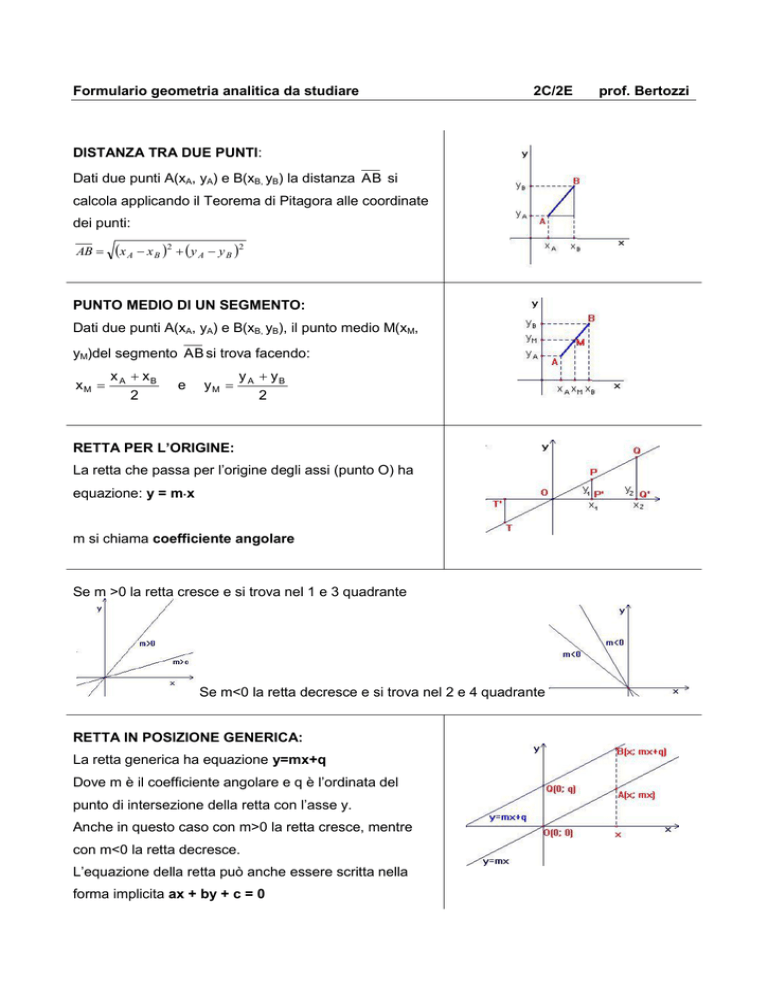
DISTANZA TRA DUE PUNTI:
Dati due punti A(xA, yA) e B(xB, yB) la distanza AB si
calcola applicando il Teorema di Pitagora alle coordinate
dei punti:
AB
x A x B 2 y A y B 2
PUNTO MEDIO DI UN SEGMENTO:
Dati due punti A(xA, yA) e B(xB, yB), il punto medio M(xM,
yM)del segmento AB si trova facendo:
xM
x A xB
2
e
yM
y A yB
2
RETTA PER L’ORIGINE:
La retta che passa per l’origine degli assi (punto O) ha
equazione: y = mx
m si chiama coefficiente angolare
Se m >0 la retta cresce e si trova nel 1 e 3 quadrante
Se m<0 la retta decresce e si trova nel 2 e 4 quadrante
RETTA IN POSIZIONE GENERICA:
La retta generica ha equazione y=mx+q
Dove m è il coefficiente angolare e q è l’ordinata del
punto di intersezione della retta con l’asse y.
Anche in questo caso con m>0 la retta cresce, mentre
con m<0 la retta decresce.
L’equazione della retta può anche essere scritta nella
forma implicita ax + by + c = 0
prof. Bertozzi
RETTE PARALLELE E RETTE PERPENDICOLARI:
Date le rette r: y=mx+q e s: y=m’x+q’
1) r è parallela a s se m m' (vuol dire che hanno lo
stesso coefficiente angolare)
2) r è perpendicolare a s se m
1
cioè m m' 1 (il
m'
m m'
m
1
m'
prodotto dei coefficienti angolari è 1).
RETTE PARTICOLARI:
1) equazione dell’asse x: y=0
2) equazione dell’asse y: x=0
3) equazione di una retta parallela all’asse x: y=k
4) equazione di una retta parallela all’asse y: x=h
5) equazione della bisettrice del 1° e del 3° quadrante:
y=x
6) equazione della bisettrice del 2° e del 4° quadrante:
y=–x
EQUAZIONE DELLA RETTA PASSANTE PER DUE
PUNTI:
Dati i punti A(xA; yA) e B(xB; yB) per trovare l’equazione
della retta passante per A e B prima si deve trovare il
coefficiente angolare della retta usando la formula
m
yB y A
e successivamente per trovare l’equazione si
xB x A
usa y y A mx x A
Dal tuo libro di testo ritrovi una sintesi di questi argomenti a pag 525 – 526 – 527 (solo
paragrafo 8)










