Rs R1 R2

Prova scritta di fine corso di Meccanica Applicata alle Macchine, modulo da 5CFU
1
1
Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC
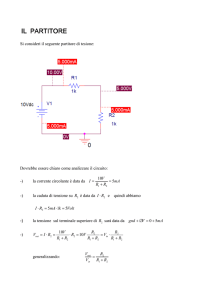
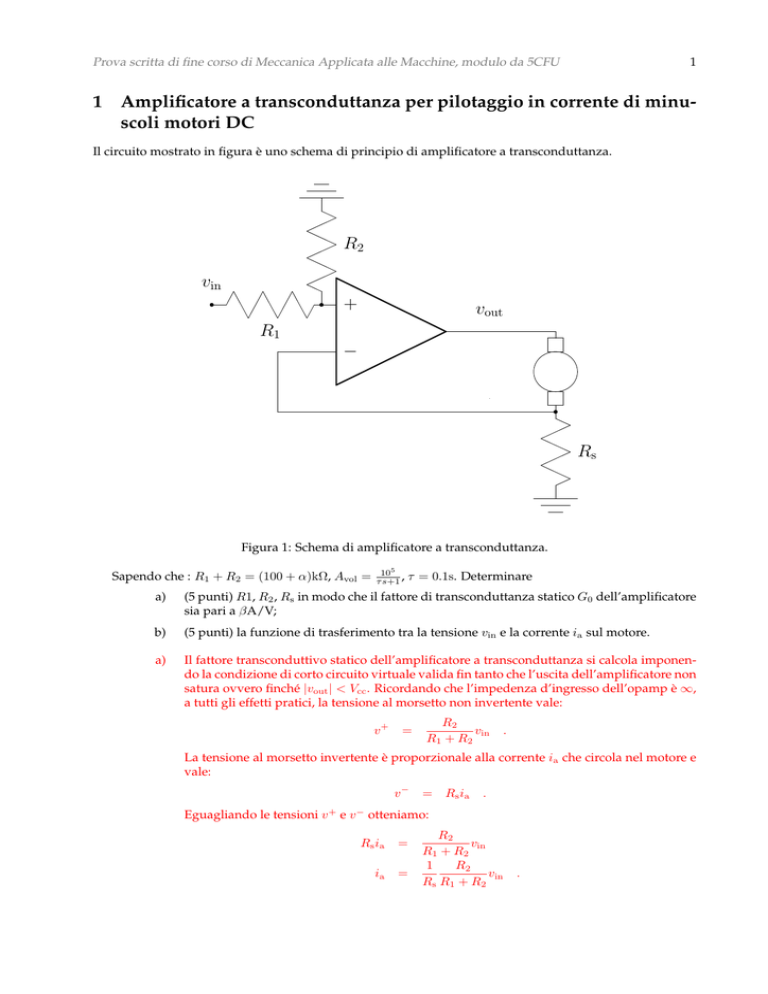
Il circuito mostrato in figura è uno schema di principio di amplificatore a transconduttanza.
R2
vin
+
vout
R1
−
Rs
Figura 1: Schema di amplificatore a transconduttanza.
Sapendo che : R1 + R2 = (100 + α)kΩ, Avol =
105
τ s+1 ,
τ = 0.1s. Determinare
a)
(5 punti) R1, R2 , Rs in modo che il fattore di transconduttanza statico G0 dell’amplificatore
sia pari a βA/V;
b)
(5 punti) la funzione di trasferimento tra la tensione vin e la corrente ia sul motore.
a)
Il fattore transconduttivo statico dell’amplificatore a transconduttanza si calcola imponendo la condizione di corto circuito virtuale valida fin tanto che l’uscita dell’amplificatore non
satura ovvero finché |vout | < Vcc . Ricordando che l’impedenza d’ingresso dell’opamp è ∞,
a tutti gli effetti pratici, la tensione al morsetto non invertente vale:
v+
=
R2
vin
R1 + R2
.
La tensione al morsetto invertente è proporzionale alla corrente ia che circola nel motore e
vale:
v−
= Rs ia
.
Eguagliando le tensioni v + e v − otteniamo:
Rs ia
=
ia
=
R2
vin
R1 + R2
1
R2
vin
Rs R1 + R2
.
1 AMPLIFICATORE A TRANSCONDUTTANZA PER PILOTAGGIO IN CORRENTE DI MINUSCOLI MOTORI DC2
Il fattore transconduttivo statico vale quindi:
G0
=
1
R2
Rs R1 + R2
Il dimensionamento di R1, R2 , Rs può essere fatto con buon senso tenendo presente che la
somma R1 + R2 è assegnata, che le resistenze devono essere tutte maggiori di zero (altrimenti avremmo inventato il moto perpetuo!) e che è opportuno che Rs sia piuttosto piccola
(dell’ordine di grandezza di 1Ω o frazione.
b)
La corrente del motore dipende dall’ingresso di riferimento vin e dalla velocità angolare
del motore che agisce come un disturbo. Per calcolare la F.d.T. del riferimento si sfrutta il
principio di sovrapposizione degli effetti imponendo ω = 0. In tal modo il motore diventa
un semplice carico ohmico-induttivo e l’impedenza vista da vout vale La s + (Ra + Rs ), da
cui:
Ia (s)
V − (s)
1
Vout (s)
La s + (Ra + Rs )
Rs
= Rs Ia (s) =
Vout (s)
La s + (Ra + Rs )
=
(1)
(2)
Sul morsetto non invertente abbiamo:
V + (s) =
R2
Vin (s)
R1 + R2
,
(3)
mentre Vout (s) vale:
¡
¢
= Avol (s) V + (s) − V − (s) .
Vout (s)
(4)
Sostituendo le equazioni (2) e (3) nella (4) otteniamo:
Vout (s)
= Avol (s)
Rs
R2
Vin (s) − Avol (s)
Vout (s) ,
R1 + R2
La s + (Ra + Rs )
(5)
da cui:
¡
Vout (s) 1 +
¢
Rs
Avol (s)
La s + (Ra + Rs )
= Avol (s)
R2
Vin (s) .
R1 + R2
(6)
Ricavando Vout (s) dall’equazione precedente e sostituendo nella (1) otteniamo:
Vout (s)
=
R2
R1 + R2
1+
Ia (s)
=
R2
R1 + R2
1
La s + (Ra + Rs )
Avol (s)
Vin (s)
Rs
La s+(Ra +Rs ) Avol (s)
Avol (s)
1+
Rs
La s+(Ra +Rs ) Avol (s)
(7)
Vin (s) ,
(8)
quindi la funzione di trasferimento cercata è:
Avol (s)
G(s) =
R2
R1 + R2
1
La s + (Ra + Rs )
=
R2
R1 + R2
Avol (s)
=
La s + (Ra + Rs ) + Rs Avol (s)
=
R2
R1 + R2
=
=
R2
R1 + R2
R2
R1 + R2
1+
Rs
La s+(Ra +Rs ) Avol (s)
A0
τ s+1
0
La s + (Ra + Rs ) + Rs τ A
s+1
=
A0
¢
=
La s + (Ra + Rs ) (τ s + 1) + Rs A0
A0
,
(Ra + Rs )(τe s + 1)(τ s + 1) + Rs A0
¡
=
(9)
(10)
(11)
(12)
(13)
2 AMPLIFICATORE CON RETROAZIONE DI TENSIONE PER PILOTAGGIO IN TENSIONE DI MINUSCOLI MOTOR
a
dove τe = RaL+R
è la costante di tempo elettrica della rete RL motore + resistenza di
s
sensing. Presumibilmente la costante di tempo τe sarà molto minore di τ quindi, in prima
approssimazione:
G(s) '
=
R2
R1 + R2
R2
R1 + R2
A0
=
(Ra + Rs )(τ s + 1) + Rs A0
A0
'
(Ra + Rs )τ s + (Ra + Rs + Rs A0 )
|
{z
}
(14)
(15)
'Rs A0
'
2
R2
R1 + R2
1
Rs
1
Ra +Rs
Rs A0 τ s
(16)
+1
Amplificatore con retroazione di tensione per pilotaggio in tensione
di minuscoli motori DC
Il circuito mostrato in figura è uno schema di principio di un amplificatore a di tensione retroazionato per
il pilotaggio in tensione di un motore DC.
R2
vin
+
vout
R1
−
Rs
Figura 2: Amplificatore di tensione retroazionato.
Sapendo che : R1 + R2 = (100 + α)kΩ, Avol =
105
τ s+1 ,
τ = 0.1s. Determinare:
a)
(5 punti) R1, R2 in modo che il guadagno statico dell’amplificatore sia pari a βV/V;
b)
(5 punti) la funzione di trasferimento tra la tensione vin e la tensione va sul motore.
a)
L’amplificatore operazionale è montato in configurazione di “buffer,” ovvero di retroazione
unitaria (fattore di retroazione = 1) quindi la tensione d’uscita, in condizioni statiche, si
3 INTEGRATORE
4
calcola come segue:
µ
vout
vout (1 + A0 )
vout
= A0 (v + − v − ) = A0
R2
vin − vout
R1 + R2
¶
(17)
R2
vin
R1 + R2
A0
R2
R2
vin '
vin
R1 + R2 1 + A0
R1 + R2
= A0
(18)
=
(19)
2
Il guadagno statico vale R1R+R
≤ 1. Non esistono quindi valori di R1 ed R2 che permettano
2
di ottenere un’amplificazione β ≥ 1.
b)
Vout (s) =
=
Vout (s)(1 + Avol (s))
=
Vout (s) =
3
Avol (s)(V + (s) − V − (s)) =
µ
¶
R2
Avol (s)
Vin (s) − Vout (s)
R1 + R2
R2
Avol (s)
Vin (s)
R1 + R2
Avol (s)
R2
Vin (s)
1 + Avol (s) R1 + R2
(20)
(21)
(22)
(23)
Integratore
Il circuito mostrato in figura può essere utilizzato per calcolare analogicamente l’integrale di un segnale.
C
R
−
vin
+
vout
Figura 3: Circuito integratore.
Sapendo che : R = (10 + α)kΩ, C = 100nF, Vcc = 15V (tensioni di alimentazione), Avol =
Determinare:
105
τ s+1 ,
τ = 0.1s.
a)
(5 punti) la funzione di trasferimento (quindi in regime lineare) tra vin e vout ;
b)
(5 punti) l’andamento temporale di vout (con condensatore inizialmente scarico) se vin (t) =
1(t).
4 AMPLIFICATORE A TRANSCONDUTTANZA PER PILOTAGGIO IN CORRENTE DI MINUSCOLI MOTORI DC5
a)
L’amplificatore retroazionato negativamente quindi vale il corto circuito virtuale e v − (t) '
v + (t) = 0. La corrente che circola in R vale i = vRin e rimane costante finché l’amplificatore
lavora in regime lineare (uscita non saturata). La tensione d’uscita vale:
q(t)
=
C
µ
¶
Z t
1
i(τ )dτ =
= −
q0 +
C
0
Z t
1
1
= − q0 −
vin (τ )dτ =
C
RC 0
1
1
Vout (s) = −
Vin (s) −
q0 .
RCs
Cs
vout (t) = −
Vout (s)
Vin (s)
La funzione di trasferimento vale quindi G(s) =
b)
4
(24)
(25)
(26)
(27)
1
= − RCs
Finché l’amplificatore non satura, la corrente in R è costante e vale i = vinR(t) = 1(t)
R . Se
il condensatore è inizialmente scarico (q0 = 0) la carica accumulata vale q(t) = i × t fino
1
a quando vout non va in saturazione. Di conseguenza vout (t) = − RC
t fino a quando non
raggiungerà la saturazione ' −vcc al tempo t∗ = vcc RC.
Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC
Il circuito mostrato in figura è uno schema di principio di amplificatore a transconduttanza.
Vin
+
Rs
Vout
−
R2
+
R1
−
R1
R2
Figura 4: Schema di amplificatore a transconduttanza.
Sapendo che : R1 + R2 = (100 + α)kΩ, Rs = 1Ω Avol =
105
τ s+1 ,
τ = 0.1s. Determinare
a)
(5 punti) R1, R2 , in modo che il fattore di transconduttanza statico G0 dell’amplificatore sia
pari a βA/V;
b)
(5 punti) la funzione di trasferimento tra la tensione vin e la corrente ia sul motore.
a)
Il fattore transconduttivo statico vale circa
G0
=
1
2
Rs R
R1
.
(28)
5 CARRO COMANDATO DA COPPIA VITE DI MANOVRA/CHIOCCIOLA
6
I tre resistori vanno calcolati con buon senso tenendo presente che Rs deve essere piccola
(rispetto alla resistenza d’armatura del motore Ra ) e rispettando il vincolo assegnato R1 +
R2 = (100 + α)kΩ.
b)
La F.d.T. tra tensione di riferimento Vin (s) e corrente d’armatura Ia (s) si può calcolare
imponendo che la velocità angolare del motore, che agisce come un disturbo, sia nulla
(principio di sovrapposizione degli effetti). Si ottiene allora:
Ia (s) =
=
=
da cui:
µ
Ia (s) 1 +
Vout (s)
=
La s + Ra + Rs
1
Avol (s)(V + (s) − V − (s))
La s + Ra + Rs
µ
¶
1
R2
Avol (s) Vin (s) − Rs Ia (s)
,
La s + Ra + Rs
R1
1
R2
Rs Avol(s)
La s + Ra + Rs
R1
¶
=
G(s) =
5
1
Avol (s)Vin (s)
La s + Ra + Rs
1+
1
La s+Ra +Rs Avol (s)
R2
1
La s+Ra +Rs Rs R1 Avol(s)
(29)
(30)
(31)
(32)
(33)
Carro comandato da coppia vite di manovra/chiocciola
Un carro di una macchina utensile viene comandato da una coppia vite di manovra/chiocciola a ricircolo
di sfere a sua volta comandato da un motoriduttore con motore DC. Sulle guide lineari del carro è presente
un attrito di tipo coulombiano fs sign(ẋ). Siano noti i seguenti parametri:
• numero di denti z1 ;
• numero di denti z2 ;
• passo della vite p;
• massa del carro m;
• momento d’inerzia del motore Ja (comprensivo della ruota 1);
• momento d’inerzia della vite Jv (comprensivo della ruota 2);
• forza d’attrito coulombiano fs ;
• costante di coppia del motore kt .
Calcolare:
a)
la corrente necessaria ad accelerare il carro con un’accelerazione desiderata ẍdes nel caso in
cui fs = 0;
b)
la corrente necessaria ad accelerare il carro con un’accelerazione desiderata ẍdes nel caso in
cui fs 6= 0.
a)
La coppia del motore viene trasformata in una spinta sul carro dal rapporto di trasmissione
z2 2π
totale zz21 2π
p , quindi la spinta sul carro vale z1 p kt ia . L’inerzia totale del sistema, ridotta
¡ z2 ¢2
¡ ¢2
+ Ja 2π
. La corrente necessaria ad
all’asse di moto del carro, vale: M = m + Jv 2π
p
p z1
accelerare il carro si trova risolvendo l’equazione:
z2 2π
kt ia
z1 p
= M ẍdes
,
(34)
5 CARRO COMANDATO DA COPPIA VITE DI MANOVRA/CHIOCCIOLA
7
z1
DC motor
z2
ẋ
-
−fs sign(ẋ)
+
¾
+
Figura 5: Carro comandato da una coppia vite di manovra/chiocciola.
ovvero:
ia
b)
M ẍdes
z2 2π
z1 p kt
=
,
(35)
Nel caso in cui sia presente l’attrito coulombiano, l’equazione (34) si modifica in:
z2 2π
kt i a
z1 p
=
M ẍdes + fs
,
(36)
e la corrente si calcola in modo analogo al caso a):
ia
=
M ẍdes + fs
z2 2π
z1 p kt
,
(37)
INDICE
8
Indice
1
Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC
1
2
Amplificatore con retroazione di tensione per pilotaggio in tensione di minuscoli motori DC
3
3
Integratore
4
4
Amplificatore a transconduttanza per pilotaggio in corrente di minuscoli motori DC
5
5
Carro comandato da coppia vite di manovra/chiocciola
6