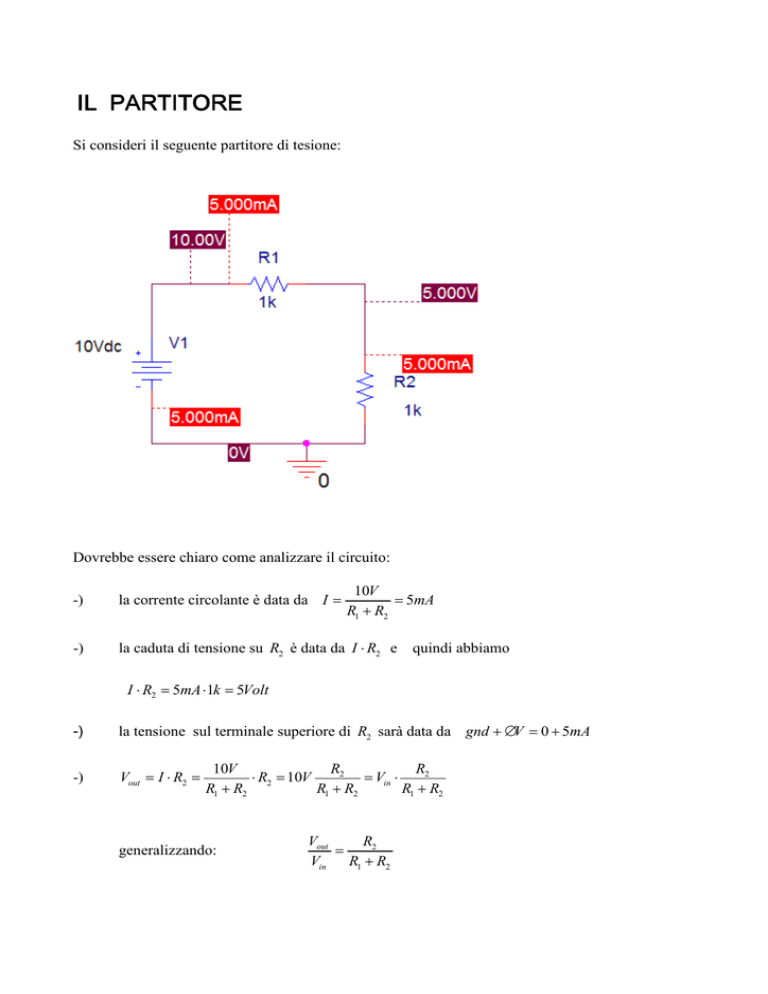
IL PARTITORE
Si consideri il seguente partitore di tesione:
Dovrebbe essere chiaro come analizzare il circuito:
10V
= 5mA
R1 + R2
-)
la corrente circolante è data da I =
-)
la caduta di tensione su R2 è data da I ⋅ R2 e quindi abbiamo
I ⋅ R2 = 5mA ⋅1k = 5Volt
-)
la tensione sul terminale superiore di R2 sarà data da gnd + ∆V = 0 + 5mA
-)
Vout = I ⋅ R2 =
10V
R2
R2
⋅ R2 = 10V
= Vin ⋅
R1 + R2
R1 + R2
R1 + R2
generalizzando:
Vout
R2
=
Vin R1 + R2
Si consideri il seguente partitore di tesione, generalizzazione di quello precedente:
Si possono applicare i passaggi della pagina precedente senza nessuna modifica.
Quindi avremo:
Vout
Z2
=
Vin Z1 + Z 2
Questa è la “formula del partitore” che verrà applicata estesamente nelle pagine seguenti.
________________________________________________________________________
N.B.
spesso si dovrà considerare la seguente situazione circuitale:
Obbligatoriamente a Z 2 andrà sostituita Z equivalente = Z 2 Z 3
Z eq
Vout
=
Vin Z1 + Z eq
N.B.
Z 3 spesso sarà l’impedenza di ingresso di uno stadio successivo.
FdT
(da saper ricavare con la massima fluidità)
Sono forniti i circuiti, le FdT finali, un punto di passaggio intermedio per le fdt complesse.
1)
2)
Filtro passa basso passivo
Risposta:
Vout
1
=
Vin 1 + sRC
Risposta:
Vout
sRC
=
Vin 1 + sRC
Filtro passa alto passivo
3)
Filtro passa basso attivo
Risposta:
4)
Filtro passa alto attivo
5)
Rete anticipatrice passiva
6)
Rete anticipatrice attiva
R2
Vout
R1
=
Vin 1 + sR2C
7)
Rete ritardatrice passiva
Risposta:
8)
(1 + s ⋅ R5 ⋅ C )
Vout
=
Vin 1 + s ( R4 + R5 )C
Rete ritardatrice attiva
fig. 1
Risposta:
Vout
=
Vin
(1 +
R1
) ⋅ (1 + s ⋅ R1 R2 ⋅ C )
R2
1 + sR1C
Per i valori del circuito in fig. 1 il diagramma di Bode del modulo è:
fig. 2
N.B. Pspice fornisce in ascissa le frquenze in hertz, nelle FdT s si esprime in pulsazioni, 2π
volte più grande della frequenza.
Con
MATLAB: