ANALISI: LIMITI E ASINTOTI
11
CONCETTO DI ASINTOTO
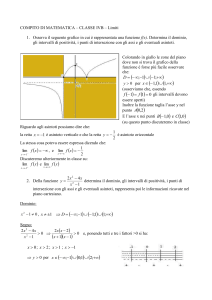
Asintoto è una retta a cui la funzione si avvicina senza mai toccarla. Una funzione può tendere all'infinito avvicinandosi
ad una retta in tre modi diversi come si può vedere dalle tre figure qui sotto
Asintoto verticale
Asintoto orizzontale
Asintoto obliquo
Asintoto verticale: quando per x che tende ad un valore finito la funzione tende all'infinito avvicinandosi ad una retta
verticale
Asintoto orizzontale: quando per x che tende all'infinito la funzione si avvicina ad una retta orizzontale
Asintoto obliquo:quando per x che tende all'infinito la funzione tende all'infinito avvicinandosi ad una retta obliqua
Osservazione: Da notare che l'asintoto orizzontale esclude l'asintoto obliquo e viceversa perché al crescere della x la
funzione può andare all'infinito in un solo modo
Asintoto verticale
Si ha un asintoto verticale quando, all'avvicinarsi della x ad un valore finito, il
valore della y cresce all'infinito
La funzione avrà valore infinito dove la non è definita, quindi per valori di x non
appartenenti al campo di esistenza
Quindi per trovare gli asintoti verticali dovremo calcolare il limite per x che tende
ai valori escludi nel dominio: supponendo che nel punto x = c la funzione non sia
definita dovremo calcolare
lim f(x) . Se il risultato vale ∞ allora la retta x = c
x →c
sarà l'asintoto verticale.
È bene, al fine di calcolare esattamente come la funzione si comporta all'infinito, calcolare sia il limite destro che il
limite sinistro per trovare il segno dell'infinito a destra e a sinistra dell'asintoto
I quattro casi possibili sono rappresentati qui sotto:
A cura della Prof.ssa Francesca Grandinetti
ANALISI: LIMITI E ASINTOTI
lim f(x) = +∞
12
lim f(x) = - ∞
x →c −
lim f(x) = + ∞
x →c −
lim f(x) = +∞
x →c −
lim f(x) = - ∞
x →c +
lim f(x) = - ∞
x →c +
x →c +
ESEMPIO: Cerchiamo, se esistono, gli asintoti verticali della funzione y =
lim f(x) = - ∞
x →c −
lim f(x) = + ∞
x →c +
3x
:
x −1
il campo di esistenza è tutti i valori reali di x tranne x = 1, valore per cui si annulla il denominatore.
calcolo lim
x →1
3x
3
= = ∞ , quindi la retta x = 1 è un asintoto verticale.
x −1 0
Per stabilire il segno di ∞, studiamo il segno della funzione y =
3x
:
x −1
3x
≥0
x −1
+
0 −
1
+
Notiamo che il segno della funzione cambia a destra e a sinistra di 1,
quindi:
lim−
x →1
3x
= −∞
x −1
e
lim+
x →1
3x
= +∞ ,
x −1
e la funzione, intorno a x=1, avrà il seguente andamento:
Asintoto orizzontale
Si ha un asintoto orizzontale quando, al crescere della x la y si avvicina ad un
valore ben determinato.
in pratica c'é l'asintoto se
lim f(x) = ℓ e l'asintoto
x →∞
sarà la retta orizzontale y = ℓ.
ESEMPIO: calcoliamo, se esiste, l'asintoto orizzontale per la funzione y =
3x
.
x −1
Calcolo il limite della funzione per x tendente ad infinito:
numeratore e denominatore hanno lo stesso grado ed il rapporto fra le x di grado
maggiore è 3, quindi lim
x →∞
3x
=3
x −1
→ La retta y = 3 sarà l'asintoto orizzontale
La funzione è la stessa che abbiamo usato per l'asintoto verticale e con i dati che
abbiamo possiamo cominciare ad abbozzarne un eventuale grafico (per tracciarlo
effettivamente mancano ancora molti dati):
A cura della Prof.ssa Francesca Grandinetti
ANALISI: LIMITI E ASINTOTI
13
Asintoto obliquo
Si ha un asintoto obliquo quando la funzione, tendendo ad infinito si avvicina
ad una retta obliqua.
Ovviamente se all’infinito la funzione ammette asintoto
orizzontale, non esisterà quello obliquo.
Vediamo quali sono le condizioni perché una funzione ammetta asintoto obliquo
della forma y = mx + q:
Prima di tutto la funzione deve tendere all'infinito per x che tende all’infinito:
lim f ( x ) = ∞
x →∞
Devono poi esistere m e q, cioè devono esistere finiti i due limiti
lim
x →∞
f (x )
=m
x
lim [f ( x ) − m ⋅ x ] = q
e
x →∞
Esempio:
Cerchiamo l’asintoto obliquo della funzione y =
3x 2 − 1
.
x
Calcolo il limite all’infinito della funzione: essendo il numeratore di grado superiore al denominatore si ha
3x 2 − 1
=∞.
x →∞
x
lim f ( x ) = lim
x →∞
Ha dunque senso chiedersi se esiste l’asintoto obliquo y = mx + q.
Cerco, se esiste, il valore del coefficiente angolare m:
f (x)
3x 2 − 1 1
3x 2 − 1
= lim
⋅ = lim
=3
x →∞ x
x →∞
x
x x →∞ x 2
m = lim
Cerco quindi q:
3x 2 − 1
3x 2 − 1 − 3x 2
−1
q = lim [f ( x ) − mx ] = lim
− 3x = lim
= lim
=0
x →∞
x →∞
x
→
∞
x
→
∞
x
x
x
Si ha quindi m = 3 e q = 0: l’asintoto obliquo è la retta y = 3x.
Nota sulla determinazione degli asintoti orizzontali od obliqui
È possibile capire se la funzione ha un asintoto orizzontale, obliquo oppure non ha asintoti di quel genere,
semplicemente osservando la forma di una funzione e riflettendo sull’ordine d’infinito:
Si avrà l’asintoto orizzontale se il numeratore e il denominatore della funzione hanno lo stesso ordine di infinito. In
questo caso il limite è uguale al rapporto tra i coefficienti dei due termini di grado più alto. Nel seguente esempio
l'ordine di infinito del numeratore e del denominatore sono entrambe uguali ad 1 (ricordiamo che la funzione log x ha
3x − 2 log x 3
=
x →∞
4x
4
ordine di infinito inferiore a qualunque x n) quindi lim
→
y=
3
è asintoto orizzontale.
4
Si avrà asintoto orizzontale anche se il numeratore ha ordine di infinito inferiore al denominatore. In questo caso il
limite vale 0: lim
x →∞
x 3 + log x
ex
=0
→
A cura della Prof.ssa Francesca Grandinetti
y = 0 è asintoto orizzontale.
ANALISI: LIMITI E ASINTOTI
14
Si avrà l’asintoto obliquo y = mx + q se nella funzione l'ordine del numeratore è superiore di uno a quello del
denominatore. Infatti per calcolare m dobbiamo fare il limite di f(x)/x : in questo modo il denominatore diventa un
infinito di un ordine superiore rispetto al denominatore di f(x), avrà quindi lo stesso ordine del numeratore ed il limite
sarà finito.
Sia, ad esempio, y =
1− x 2
. Le funzioni (1 –x2) e (x) hanno rispettivamente ordine d’infinito 2 e 1. si avrà, quindi
x
1− x 2 1
1− x 2
1− x 2 + x 2
1− x 2
1
⋅ = lim
=
−
1
,
q
=
lim
−
(
−
x
)
=
lim
= lim = 0
2
x →∞ x
x →∞
x →∞
x →∞
x
x x →∞ x
x
x
l’asintoto obliquo: m = lim
→
y = − x è l’asintoto obliquo.
Non si avranno asintoti orizzontali né obliqui se l'ordine del numeratore è superiore a quello del denominatore di più di
uno.
ESEMPI:
•
y=
3x
x −1
ha un asintoto orizzontale perché numeratore e denominatore hanno entrambi grado uno ed il rapporto
fra i coefficienti dei termini di grado più alto è 3/1 = 3 quindi y = 3
è l’asintoto orizzontale
•
y=
•
y=
x −1
x2
3x 2 − 1
2x
ha asintoto orizzontale y = 0 poiché il grado del numeratore è inferiore a quello del denominatore
ha un asintoto obliquo perché il grado del numeratore è due e quello del denominatore è uno
quindi quando farò f(x)/x otterrò una frazione con lo stesso grado al numeratore e al denominatore (m = 3/2)
•
y=
3x 4 + 5
2x
non ha asintoto orizzontale né obliquo
ESERCIZI
Dopo aver determinato il dominio, il segno e le intersezioni con gli assi delle seguenti funzioni, determinare gli
eventuali asintoti, verticali e orizzontali o obliqui:
y=
y=
y=
x +3
x + 4x + 4
2
x +3
x
x2 −4
x
y=
y=
y=
x3
1− x
2
x 2 −1
2x + 3
ln(4 − 2x )
x + 3x + 4
2
y=
y=
5+ x2
x −4
2
x 2 − 4x + 1
2x
x +3
y=e
A cura della Prof.ssa Francesca Grandinetti
x 2 −4
x2
y=
y = x 2 −1
x2 −9
y = ln
x +1
x−2
y=
2
y=
ex
ln( x + 2)
y=
9 − 3x
ex
2x + 4
ln(2x + 5)