COMPITO DI MATEMATICA – CLASSE IVB – Limiti
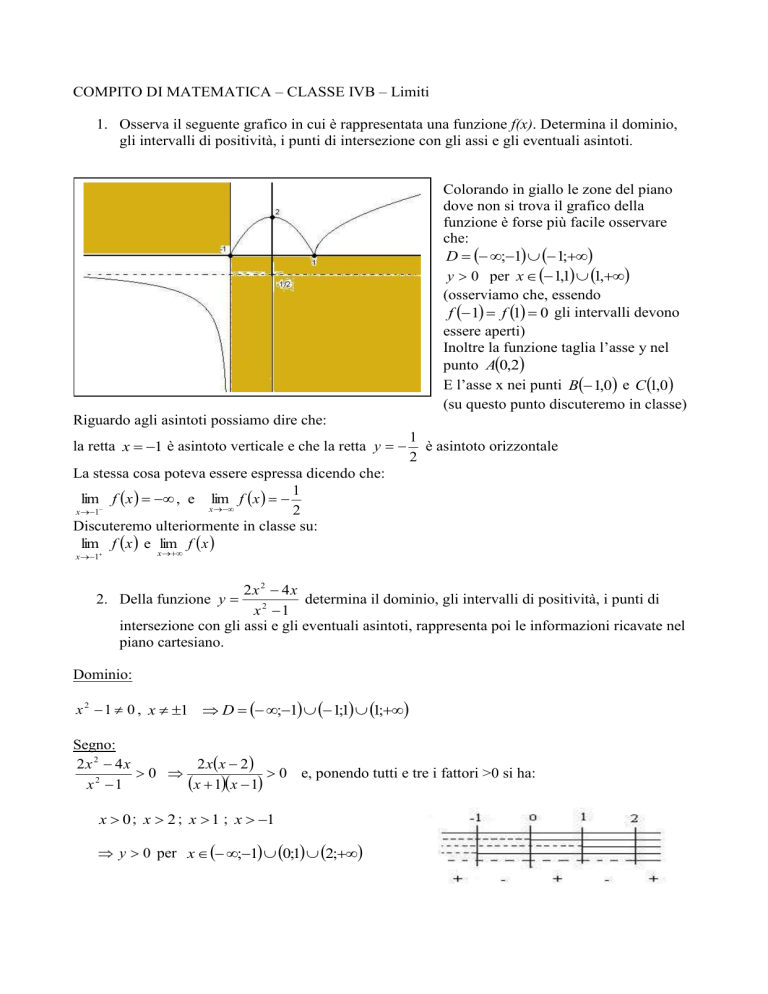
1. Osserva il seguente grafico in cui è rappresentata una funzione f(x). Determina il dominio,
gli intervalli di positività, i punti di intersezione con gli assi e gli eventuali asintoti.
Colorando in giallo le zone del piano
dove non si trova il grafico della
funzione è forse più facile osservare
che:
D ;1 1;
y 0 per x 1,1 1,
(osserviamo che, essendo
f 1 f 1 0 gli intervalli devono
essere aperti)
Inoltre la funzione taglia l’asse y nel
punto A0,2
E l’asse x nei punti B 1,0 e C 1,0
(su questo punto discuteremo in classe)
Riguardo agli asintoti possiamo dire che:
la retta x 1 è asintoto verticale e che la retta y
1
è asintoto orizzontale
2
La stessa cosa poteva essere espressa dicendo che:
1
lim f x , e lim f x
x
2
x 1
Discuteremo ulteriormente in classe su:
lim f x e lim f x
x
x 1
2x 2 4x
determina il dominio, gli intervalli di positività, i punti di
x2 1
intersezione con gli assi e gli eventuali asintoti, rappresenta poi le informazioni ricavate nel
piano cartesiano.
2. Della funzione y
Dominio:
x 2 1 0 , x 1 D ;1 1;1 1;
Segno:
2 x x 2
2x 2 4x
0
0 e, ponendo tutti e tre i fattori >0 si ha:
2
x 1x 1
x 1
x 0 ; x 2 ; x 1 ; x 1
y 0 per x ;1 0;1 2;
Intersezioni con gli assi:
2x 2 4x
y
Con l’asse x:
x 2 1 dai passaggi precedenti si hanno i punti di coordinate B2,0 e O
y 0
Con l’asse y non è necessario calcolarlo poiché risulta essere l’origine che abbiamo già individuato
sopra. (Vi ricordo che una funzione può avere un solo punto d’incontro con l’asse delle ordinate.
Perché?)
Riportiamo sul piano cartesiano le informazioni ottenute, con la convenzione che risultano colorate
le zone dove non si troverà in grafico della funzione:
Passiamo ora allo studio dei limiti per conoscere il comportamento della funzione agli estremi del
dominio.
2x 2 4x
x
x2 1
lim
, dunque dovremmo procedere al calcolo come visto in classe,
ma, sempre per quanto abbiamo visto in classe, si può anche dire che, essendo il grado del
numeratore uguale a quello del denominatore si ha:
il limite si presenta nella forma
2x 2 4x
2x 2 4x
2
lim
2
e,
analogamente,
x
x
x2 1
x2 1
lim
cioè il limite è il rapporto tra i coefficienti dei termini di grado massimo.
Siamo dunque nel caso in cui la funzione ha un asintoto orizzontale (è quindi esclusa la ricerca di
un asintoto obliquo).
numero
Passiamo ora al calcolo degli altri quattro limiti che si presentano nella forma
, per cui
0
abbiamo:
lim
x 1
lim
x 1
2x 2 4x
x2 1
2x 2 4x
x2 1
lim
2x 2 4x
x2 1
lim
2x 2 4x
x2 1
x 1
x 1
(per il segno di ci rifacciamo al precedente studio del segno)
Dai due limiti sopra possiamo dedurre che le rette x 1 e x 1 sono asintoti verticali per la
funzione.
Aggiungiamo anche queste informazioni nel grafico:
E qui l’esercizio per voi era finito. Per soddisfare la curiosità di alcuni, riporto il grafico completo
della funzione, che fra non molto anche voi sarete in grado di disegnare:
3. Spiega quali sono le condizioni per cui una funzione y f x ha un asintoto verticale, un
asintoto orizzontale o un asintoto obliquo. Una funzione il cui dominio è l’insieme
D 2;9 può avere asintoti? E se il dominio fosse l’insieme D 2;9 ? Motiva la tua
risposta.
Questo esercizio andava svolto in due parti: la prima parte chiedeva semplicemente di riassumere le
condizioni per l’esistenza di asintoti per una funzione, che sono le seguenti:
lim f x la funzione ha un asintoto verticale di equazione x x0
x x0
lim f x l la funzione ha un asintoto orizzontale di equazione y l
x
Vi faccio notare, per n-esima volta che le due condizioni sopra esposte sono sufficienti per
l’esistenza di un asintoto verticale o orizzontale, mentre la seguente è solo necessaria per l’esistenza
di un asintoto obliquo!
lim f x
x
la certezza dell’esistenza dell’asintoto obliquo è data dalla possibilità che esistano (cioè che il loro
valore sia un numero) i due seguenti limiti, che ci danno i coefficienti della retta asintoto
y mx q :
m lim
x
f x
x
q lim f x mx
x
La seconda parte del quesito chiedeva di mettere in gioco le vostre conoscenze.
Consideriamo prima il caso di asintoti orizzontali o obliqui.
In entrambi i casi si tratta di capire il comportamento della funzione all’infinito, ma la funzione
dell’esercizio è definita in D 2;9 o in D 2;9 che sono due intervalli limitati, il primo
contiene anche gli estremi, x 2 e x 9 , il secondo no. Questo significa che la nostra funzione
sta tutta nella striscia tra –2 e 9, niente a destra, niente a sinistra di tale striscia, dunque non ha senso
andare a studiarne il comportamento all’infinito e dunque nessun asintoto orizzontale o obliquo.
Consideriamo il caso degli asintoti verticali.
Se D 2;9 è ovvio che non può esserci asintoto verticale, perché, se ci fosse, dovrebbe esserci
un punto x0 D in cui lim f x , ma i punti del dominio, vi ricordo, sono punti in cui si può
x x0
calcolare il valore della funzione, cioè, tutti quei punti in cui f(x) assume un valore ben definito, un
numero, ma non è un numero! Dunque in questo caso non potevano esserci asintoti verticali.
Se invece D 2;9, potevano succedere che gli asintoti verticali ci fossero. Infatti per tutti i
punti interni al dominio, valgono le considerazioni viste sopra, ma negli estremi x 2 e x 9 , la
funzione non è definita e dunque potrebbe verificarsi che
lim f x e/o lim f x
x 2
x 9