Il multivibratore astabile con trigger di Schmitt invertente Frequenza

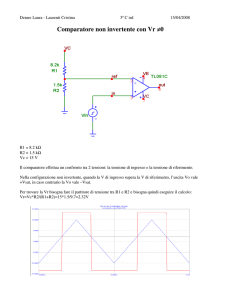
Il multivibratore astabile con trigger di Schmitt invertente
I multivibratori sono circuiti che si possono trovare in uno di due stati possibili: livello logico alto o
livello logico basso. Nei multivibratori astabili nessuno dei due stati è stabile quindi l’uscita
commuta continuamente tra uno stato e l’altro. Si utilizza come generatore di onda quadra.
Il circuito di figura rappresenta un multivibratore astabile con trigger di Schmitt invertente.
Figura 1 Il multivibratore astabile con trigger di Schmitt invertente.
Il segnale applicato al morsetto invertente deriva dalla carica e scarica del condensatore C attraverso
la resistenza R. Per analizzare il funzionamento di questo circuito supponiamo che il condensatore
sia scarico e che l’uscita sia +VSAT. Il condensatore inizia a caricarsi attraverso la resitenza R per
raggiungere la tensione +VSAT ma, non appena Vc (tensione ai capi del condensatore e tensione di
ingresso del trigger) supera la tensione di soglia superiore del trigger data da:
𝑉𝑇𝐻 =
𝑅2
𝑉 = 𝛽𝑉𝑆𝐴𝑇
𝑅1 + 𝑅2 𝑆𝐴𝑇
l’uscita Vout commuta a –VSAT ed il condensatore si scarica per raggiungere il valore della tensione
–VSAT. Non appena Vc diventa minore della tensione inferiore del trigger data da:
𝑉𝑇𝐿 = −
𝑅2
𝑉 = −𝛽𝑉𝑆𝐴𝑇
𝑅1 + 𝑅2 𝑆𝐴𝑇
l’uscita Vout commuta a +VSAT e il condensatore comincia nuovamente a caricarsi.
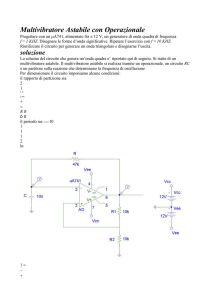
In uscita otteniamo un’onda quadra (vedi figura 2).
Frequenza dell’onda quadra in uscita.
Per prima cosa calcoliamo il tempo che impiega un condensatore per caricarsi da una tensione V1 ad
una tensione V2 con V1<V2.
Ricordiamo che un condensatore scarico si carica alla tensione VC seguendo la seguente legge
esponenziale:
𝑡
𝑉𝐶 = 𝑉𝑖𝑛 (1 − 𝑒 −𝜏 )
dove Vin è la tensione di ingresso del condensatore, si trova:
𝑡1
𝑉1 = 𝑉𝑖𝑛 (1 − 𝑒 − 𝜏 )
1
Troviamo t1:
𝑡1
𝑉1 = 𝑉𝑖𝑛 − 𝑉𝑖𝑛 𝑒 − 𝜏
−
→
𝑡1
𝑉1 − 𝑉𝑖𝑛 = −𝑉𝑖𝑛 𝑒 − 𝜏
𝑡1
𝑉𝑖𝑛 − 𝑉1
= 𝑙𝑛
𝜏
𝑉𝑖𝑛
→
→
𝑡1 = −𝜏 𝑙𝑛 (1 −
𝑡1
𝑉𝑖𝑛 − 𝑉1
= 𝑒− 𝜏
𝑉𝑖𝑛
𝑉1
)
𝑉𝑖𝑛
Con lo stesso procedimento determiniamo:
𝑡2 = −𝜏 𝑙𝑛 (1 −
𝑉2
)
𝑉𝑖𝑛
Ma allora il tempo impiegato dal condensatore per caricarsi dalla tensione V1 alla tensione V2 vale:
𝑇 = 𝑡2 − 𝑡1 = −𝜏 𝑙𝑛 (1 −
𝑉2
𝑉1
𝑉𝑖𝑛 − 𝑉1
𝑉𝑖𝑛 − 𝑉2
) + 𝜏 𝑙𝑛 (1 − ) = 𝜏 [𝑙𝑛 (
) − 𝑙𝑛 (
)] =
𝑉𝑖𝑛
𝑉𝑖𝑛
𝑉𝑖𝑛
𝑉𝑖𝑛
= 𝜏 𝑙𝑛 (
𝑉𝑖𝑛 − 𝑉1
𝑉𝑖𝑛 − 𝑉1
) = 𝑅𝐶 𝑙𝑛 (
)
𝑉𝑖𝑛 − 𝑉2
𝑉𝑖𝑛 − 𝑉2
Figura 2 Segnale di uscita del condensatore (ingresso del triggre) e segnale in uscita del circuito.
Utilizzando la relazione appena trovata calcoliamo il periodo dell’onda quadra.
Il tempo impiegato dal condensatore per caricarsi dalla tensione –βVSAT alla tensione βVSAT si trova
sostituendo all’espressione appena trovata:
Vin=VSAT
V1=-β VSAT
V2=β VSAT
2
𝑇1 = 𝑅𝐶 𝑙𝑛
𝑉𝑆𝐴𝑇 + 𝛽𝑉𝑆𝐴𝑇
1+𝛽
= 𝑅𝐶 𝑙𝑛
𝑉𝑆𝐴𝑇 − 𝛽𝑉𝑆𝐴𝑇
1−𝛽
analogamente si trova il tempo impiegato dal condensatore per scaricarsi dalla tensione βVSAT alla
tensione -βVSAT si trova sostituendo all’espressione già utilizzata1:
Vin=VSAT
V1=-β VSAT
V2=β VSAT
𝑇2 = 𝑅𝐶 𝑙𝑛
𝑉𝑆𝐴𝑇 + 𝛽𝑉𝑆𝐴𝑇
1+𝛽
= 𝑅𝐶 𝑙𝑛
𝑉𝑆𝐴𝑇 − 𝛽𝑉𝑆𝐴𝑇
1−𝛽
Finalmente troviamo il periodo dell’onda quadra:
𝑇 = 𝑇1 + 𝑇2 = 2𝑅𝐶 𝑙𝑛
1+𝛽
1−𝛽
Di conseguenza la frequenza del segnale vale:
𝑓=
1
1
=
𝑇 2𝑅𝐶 𝑙𝑛 1+𝛽
1−𝛽
Questo file può essere scaricato gratuitamente. Se pubblicato citare la fonte.
Matilde Consales
1
Ricordiamo che deve essere sempre V1<V2
3