Circuito capacitivo in corrente alternata
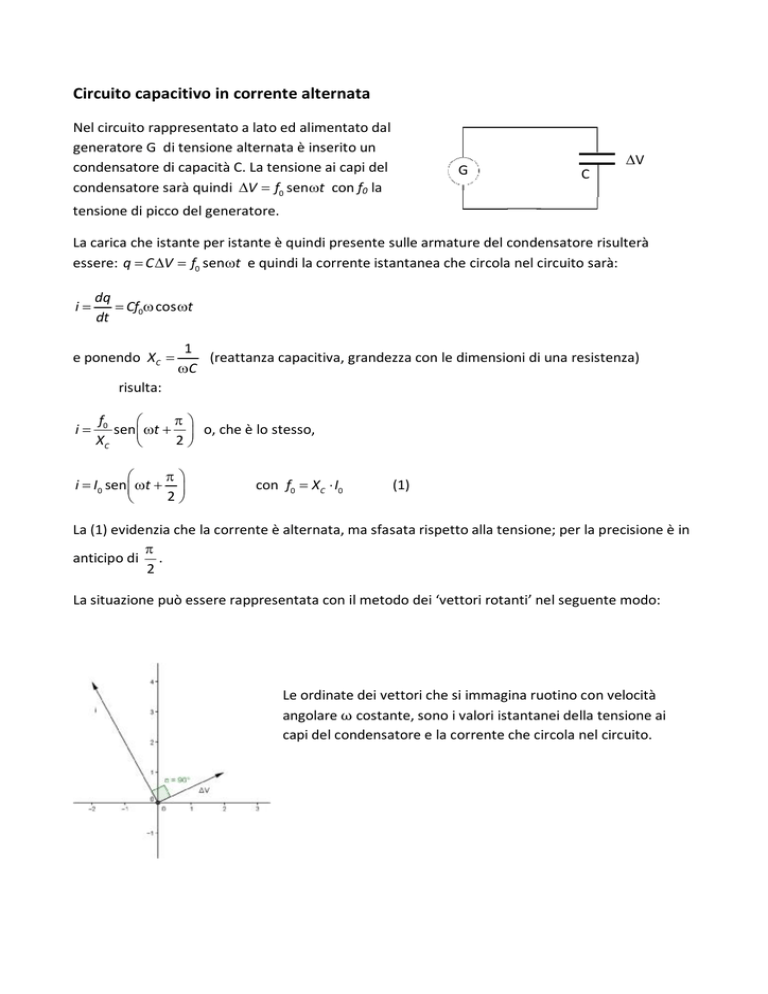
Nel circuito rappresentato a lato ed alimentato dal
generatore G di tensione alternata è inserito un
condensatore di capacità C. La tensione ai capi del
condensatore sarà quindi ∆V = f0 senωt con f0 la
G
C
∆V
tensione di picco del generatore.
La carica che istante per istante è quindi presente sulle armature del condensatore risulterà
essere: q = C ∆V = f0 senωt e quindi la corrente istantanea che circola nel circuito sarà:
i=
dq
= Cf0ω cos ωt
dt
e ponendo XC =
1
(reattanza capacitiva, grandezza con le dimensioni di una resistenza)
ωC
risulta:
i=
f0
π
sen ωt + o, che è lo stesso,
XC
2
π
i = I0 sen ωt +
2
con f0 = XC ⋅ I0
(1)
La (1) evidenzia che la corrente è alternata, ma sfasata rispetto alla tensione; per la precisione è in
π
anticipo di .
2
La situazione può essere rappresentata con il metodo dei ‘vettori rotanti’ nel seguente modo:
Le ordinate dei vettori che si immagina ruotino con velocità
angolare ω costante, sono i valori istantanei della tensione ai
capi del condensatore e la corrente che circola nel circuito.












