la soluzione a cura del prof. ing. Zefferino Pavanelli

Soluzione SECONDA PROVA SCRITTA di ELETTRONICA, TELECOMUNICAZIONI E APPLICAZIONI per gli Istituti
Professionali Statali (IPSIA)
Prof. Zefferino Pavanelli docente di elettronica presso ITIS Gastaldi – Giorgi di Genova.
Per rendere possibili le specifiche richieste la tensione di alimentazione duale è +12V e -12V
Dato che le resistenze R1,R2,R3 ed R4 sono tutte uguali ad R l’amplificatore A1 ha un guadagno pari a 2
Dovendo la tensione di uscita da A1 variare da +3V a +9V la tensione sull’ingresso non invertente di A1 che
è anche la tensione sul condensatore C dovrà variare da 1,5V a 4,5V
La corrente fornita dal generatore Vin è espressa dalla relazione:
i1 
(5  Vc)
R1
La corrente fornita dal generatore all’A.O1 tramite R2 è espressa dalla relazione:
i2 
2Vc  Vc
R2
La corrente totale di carica del condensatore, sapendo che i denominatori R1 ed R2 sono uguali risulta non
dipendere dalla tensione Vc assunta dal condensatore nel tempo, ed è espressa dalla relazione:
i
5  Vc  2Vc  Vc 5

R
R
Sapendo che la tensione a capi del condensatore è legata alla corrente in ingresso dalla rlazione:
dV 
dQ 1
 idt
C
C
e che la variazione complessiva da 1,5V a 4,5V si ottiene durante l’intero periodo della forma d’onda
triangolare pari a 0,002 secondi si ottiene la relazione:
4,5  1,5 
5
0,002
CR
Posto R=10K il valore della capacità C necessario per ottenere la frequenza di 500 Hz risulta:
C
5
* 2 *10 3  3,33 *10 7  333nF
4
3 *10
L’A.O2 è un comparatore con memoria (trigger di Schmitt) dimensionato in moto tale che quando la
tensione di uscita dall’A.O1 V1 arriva a +9V la tensione sull’ingresso non invertente di A.O2 supera la Vrif
determinando il passaggio di Vout da –Vsat a + Vsat che agendo sul transistor BJT provoca la scarica rapida
del condensatore C fino ala tensione minima di +1,5V; a quel punto la tensione in uscita da A.O.1 si abbassa
a +3V e lo stesso circuito dell’A.O.2 deve a quel punto commutare l’uscita a –Vsat bloccando la scarica del
condensatore che può quindi ricaricarsi.
Al punto iniziale della rampa (V1=+3V) vale seguente la relazione sul partitore di tensione costituito dalle
esistenza R7 ed R8:
93
* R7  3  Vrif
R7  R8
Al punto finale superiore della rampa (V1=+9V) sullo stesso partitore di tensione costituito dalle esistenza
R7 ed R8 vale seguente la relazione:
9
9  (9)
* R7  Vrif
R7  R8
Tale sistema di equazioni è risolvibile rispetto alle incognite X e Vrif essendo l’incognita X pari a:
X 
R7
R7  R8
La soluzione porta ad un valore di Vrif=4,5V e ad un valore di X=0,25; posto R8=10K il valore di R7 risulta
pari a 3,3 K
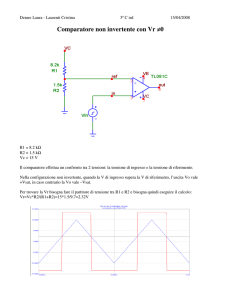
Le forme d’onda risultano:
Genova 27 Giugno 2009