Soluzioni

Seconda puntata della gara a squadre.
8 Gennaio 2004
Soluzioni.
Quesito 1
Un cubo K di volume 1 contiene un poliedro convesso M. La proiezione perpendicolare
di M su ogni faccia di K coincide con la faccia stessa. Qual è il più piccolo volume
possibile di M?
Soluzione
La proprietà, che la proiezione perpendicolare di M coincida con la faccia di V su cui si
proietta, è equivalente al fatto che M intersechi ogni spigolo di K. Si scelga un punto
appartenente a M su ogni spigolo di K, e sia M′ la chiusura convessa di questi 12 (non
necessariamente distinti) punti. M′ è quindi un poliedro convesso contenuto in M e
soddisfacente la stessa proprietà. Si osservi che M′ è ottenuto da K asportando, per ogni
vertice V di K, la piramide avente vertici in V e in quelli, tra i 12 punti individuati
precedentemente, che si trovano sui tre spigoli di K concorrenti in V (si noti che alcune di
queste piramidi possono essere degeneri, nel caso che alcuni dei 4 punti così individuati
vengano a coincidere). Sia pari a 1 la lunghezza dello spigolo e siano F e G due facce
opposte di K. Il volume totale di tutte le piramidi escisse da K e aventi base giacente su F
può essere maggiorato nel modo seguente: poichè le piramidi in questione sono disgiunte,
la somma delle aree delle loro basi è al più uguale all’area di F, cioè 1, e l’altezza di ogni
piramide è al più 1, quindi il volume totale di dette piramidi è al più 13 . La stessa
maggiorazione vale ovviamente per le piramidi aventi base su G; poichè ogni piramide
escissa da K per ottenere M′ ha base su F o su G, il volume totale di tutte queste piramidi è
al più 23 , dunque il volume di M′ è almeno 13 . Infine, un M con volume 13 è dato dalla
chiusura convessa di 4 vertici non adiacenti di K: in questo caso M è un tetraedro regolare
ed è facile vedere, o mediante un argomento simile a quello dato precedentemente, o
calcolando direttamente la lunghezza dello spigolo di M, che il suo volume è infatti 13 , che
è anche la risposta al problema.
Quesito 2
Determinare la minima area di un pentagono convesso avente i vertici con coordinate
intere.
Puó essere utile sfruttare la seguente formula, chiamata Teorema di Pick: se un
poligono ha i vertici con coordinate intere la sua area coincide con A  B/2 − 1 dove A
indica il numero di punti interni al poligono con coordinate intere e B il numero di punti
che stanno sulla frontiera del poligono e hanno coordinate intere.
Soluzione.
Riportiamo la soluzione che ci ha inviato la squadra del Liceo Scientifico Galileo
Galilei di Dolo (Venezia).
Dimostriamo innanzitutto che un poligono di 5 lati contiene al suo interno almeno un
punto del reticolo (chiamiamo reticolo l’insieme dei punti del piano aventi coordinate
intere).
Chiamiamo x 1 , x 2 , x 3 , x 4 , x 5 le ascisse (intere) dei 5 punti e y 1 , y 2 , y 3 , y 4 , y 5 le rispettive
ordinate. Consideriamo ora le congruenze modulo 2 delle ascisse. Per il "principio dei
cassetti", possiamo trovare 3 ascisse appartenenti alla stessa classe di resto modulo 2. Ma
sempre per lo stesso principio, considerando le rispettive ordinate di questi 3 punti, posso
trovare 2 ordinate appartenenti alla stessa classe di congruenza modulo 2.
Ciò sta a indicare che possiamo trovare una coppia di punti (diciamo A e B) che hanno
le ascisse e le ordinate con la stessa parità e questo significa che il punto medio del
segmento che li unisce appartiene al reticolo e appartiene anche al poligono grazie alla
convessità.
Distinguiamo ora due casi. Il punto medio può appartenere ad un lato del pentagono o
può essere interno al pentagono.
Se il punto è interno al pentagono, ossia appartiene a una delle diagonali, abbiamo
dimostrato ciò che intendevamo dimostrare. Se esso appartiene invece a un lato,
consideriamo il pentagono avente vertici MBCDE (M è il punto medio di AB) . Esso è
convesso e ha area minore di ABCDE. Possiamo reiterare il procedimento fino ad ottenere
un pentagono convesso privo di lati aventi punti appartenenti al reticolo, eccettuati i vertici.
A questo punto certamente un punto è interno al pentagono per quanto visto sopra.
È ora banale risolvere il problema iniziale. Per il Teorema di Pick, poichè il pentagono
ha almeno 5 vertici appartenenti al reticolo e almeno un punto del reticolo ad esso interno,
l’area vale almeno 52  1 − 1  52 .
Quesito 3
Dimostrare che ogni potenza di 5 ha un multiplo nella cui rappresentazione decimale
non compare la cifra 0.
Soluzione.
Consideriamo una potenza di 5, sia 5 p . Se la sua rappresentazione decimale non
contiene zeri siamo a posto, nell’altro caso sia r ≥ 1 il numero di cifre che compaiono a
destra dell’ultimo zero di 5 p . Consideriamo ora il numero 5 p 10 r  1 : il numero di cifre
che compaiono a destra del suo ultimo zero è per lo meno r  1 dato che termina con le
stesse r cifre del precedente e la cifra al posto r  1 è non nulla in quanto è pari a 5.
Procediamo nello stesso modo fin quando troveremo un multiplo n5 p le cui ultime p cifre
sono tutte non nulle. Sia ora m il resto della divisione di n con 2 p , cioè valga n  k2 p  m
con 0 ≤ m  2 p . Si ha
m5 p  n5 p − k10 p
e quindi m5 p e n5 p hanno le stesse p cifre finali e dato che m5 p ha al massimo di p cifre
essendo minore di 2 p 5 p , abbiamo trovato un multiplo di 5 p senza zeri nella sua
rappresentazione decimale.
Quesito 4
Consideriamo l’insieme A formato da tutti gli interi da 1 a p :
A  1 , 2 , … , p .
Eseguiamo cancellazioni successive, procedendo ad ogni passo secondo la seguente regola:
scegliamo un numero k in A fra quelli non ancora cancellati e cancelliamo tutti i numeri
che dividono k  p.
Determinare tutti i numeri primi p per i quali, seguendo questo procedimento, sia possibile
cancellare tutti i numeri di A.
Soluzione.
Dimostriamo che gli unici primi con la proprietà richiesta sono i numeri 2 e 3. Se
p ∈ 2, 3, scegliendo il numero p, vengono cancellati i divisori di 2p, cioè tutti gli
elementi di A.
Consideriamo ora un primo p ≥ 5 e dimostriamo che in questo caso non è possibile
cancellare tutti i numeri di A. Procedendo per assurdo, supponiamo che ciò sia possibile in
n passi, scegliendo successivamente i numeri k 1 , k 2 , … , k n . (Ovviamente possiamo
supporre che ad ogni passo sia stato cancellato almeno un numero, altrimenti quel passo
sarebbe stato inutile.)
Necessariamente n  1 perché altrimenti k 1  p dovrebbe essere multiplo di tutti gli
elementi di A, in particolare k 1  p sarebbe multiplo di 3p che è, però, maggiore di k 1  p.
L’ultima scelta, quella di k n , deve cancellare k n stesso, per cui k n divide k n  p. Ma ciò
implica che k n |p, da cui k n  p (ovviamente k n ≠ 1 perchè l’1 è stato cancellato subito nel
primo passo). Di conseguenza, l’ultima scelta può aver cancellato soltanto dei divisori di 2p
diversi da 1. In altre parole, dopo la penultima cancellazione è rimasto non cancellato p ed
eventualmente il 2. Consideriamo separatamente questi due casi.
(a) Se prima dell’ultima scelta fosse rimasto non cancellato soltanto il numero p, anche la
scelta di k n−1 avrebbe cancellato k n−1 stesso, da cui (come prima) k n−1 |p. Visto che
k n−1 ≠ p  k n , si avrebbe k n−1  1. In tal caso sarebbe n  2 (perché l’1 viene
cancellato nel primo passo) e tutti i numeri 1, 2, … , p − 1 dividerebbero p  1; ma
p1
2
p − 1 non può dividere p  1 perchè il numero p−1  1  p−1
non è intero se p ≥ 5.
(b) Dal punto (a) segue che, prima dell’ultima scelta sono rimasti non cancellati i due
numeri 2 e p, e la scelta di k n−1 non ha cancellato k n−1 stesso. Necessariamente
p2
3
non intero, il numero p − 1 è stato cancellato prima
k n−1  2. Essendo p−1  1  p−1
del penultimo passo, cioè con la scelta di un k i con i  n − 1. Essendo
p  ki
2p
1

 2  2  3,
p−1
p−1
p−1
necessariamente p  k i  2p − 1, ma ciò implica che, con la scelta di k i , è stato
cancellato anche il 2, una contraddizione.
Quesito 5
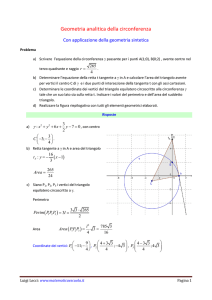
Dato un quadrato ABCD, sia k la circonferenza costruita sul diametro AB. Sia t 1 la retta
tangente a k dal punto C (diversa dalla retta BC); essa interseca AD nel punto P. Sia t 2 la
retta tangente comune esterna (diversa dalla retta AD) della circonferenza k e la
circonferenza inscritta nel triangolo CDP. Dimostrare che le rette t 1 e t 2 sono
perpendicolari.
Soluzione
La soluzione seguente è quella che ci ha inviato l’Istituto tecnico agrario statale di
Limbiate (Milano). Purtroppo questa "dimostrazione" presenta un grosso errore che mi ha
segnalato Giovanni Viglietta di Fossano (Cuneo) e che mi aveva completamente ingannato:
lascio al lettore il gusto di scoprire dove sta la pecca.
Tracciamo la bisettrice dell’angolo DJC, che passa per l’incentro O del triangolo DCJ;
tracciamo i raggi OM,OL perpendicolari a t 1 e t 2 nei punti di tangenza e i raggi ON e OK
perpendicolari ai lati nei punti di tangenza. I triangoli ONH e OLH sono uguali avendo i tre
lati uguali e analogamente i triangoli OKJ e OMJ sono fra loro uguali. Quindi i due
triangoli JDH e JXH risultano uguali avendo uguali gli angoli in J e in H e avendo il lato
JH in comune. Questo significa che l’angolo JXH è retto come lo è l’angolo in D, cioè le
rette t 1 e t 2 sono perpendicolari.
Vediamo ora una dimostrazione corretta e il corrispondente disegno.
Possiamo supporre che il quadrato sia di lato unitario. Determiniamo prima il raggio
della circonferenza k ′ inscritta nel triangolo CDP. Siano Q il punto del segmento BC tale
che PQ sia parallelo a AB, e T il punto comune di k e PC . Allora x : PA  PT e
CT  CB  1. Il triangolo PQC è rettangolo, per cui 1  1 − x 2  1  x 2 . Ne segue che
x  1/4.
È noto che l’area di un triangolo di lati a, b, c è uguale a 12 a  b  c , dove  è il
raggio della circonferenza inscritta nel triangolo. Applicando questa formula al triangolo
CDP, otteniamo facilmente che il raggio di k ′ vale 1/4.
Denotiamo con M e N il punto medio rispettivamente di AD e di BC, e con O e O ′ il
centro rispettivamente di k e di k ′ . Essendo il raggio di k ′ uguale a 1/4, la retta MN è
tangente a entrambe le circonferenze k e k ′ . Rispetto alla retta OO ′ , la retta t 1 è simmetrica
alla MN e la retta t 2 è simmetrica alla AD. Di conseguenza, l’angolo fra t 1 e t 2 ha la stessa
ampiezza dell’angolo fra MN e AD, cioè 90 ∘ .