Geometria analitica della circonferenza

Geometria analitica della circonferenza
Con applicazione della geometria sintetica
Problema
a) Scrivere l’equazione della circonferenza  passante per i punti A(1;0), B(0;2) , avente centro nel
265
.
4
terzo quadrante e raggio r 
b) Determinare l’equazione della retta t tangente a  in A e calcolare l’area del triangolo avente
per vertici il centro C di  e i due punti di intersezione della tangente t con gli assi cartesiani.
c) Determinare le coordinate dei vertici del triangolo equilatero circoscritto alla circonferenza 
tale che un suo lato sia sulla retta t. Indicare i valori del perimetro e dell’area del suddetto
triangolo.
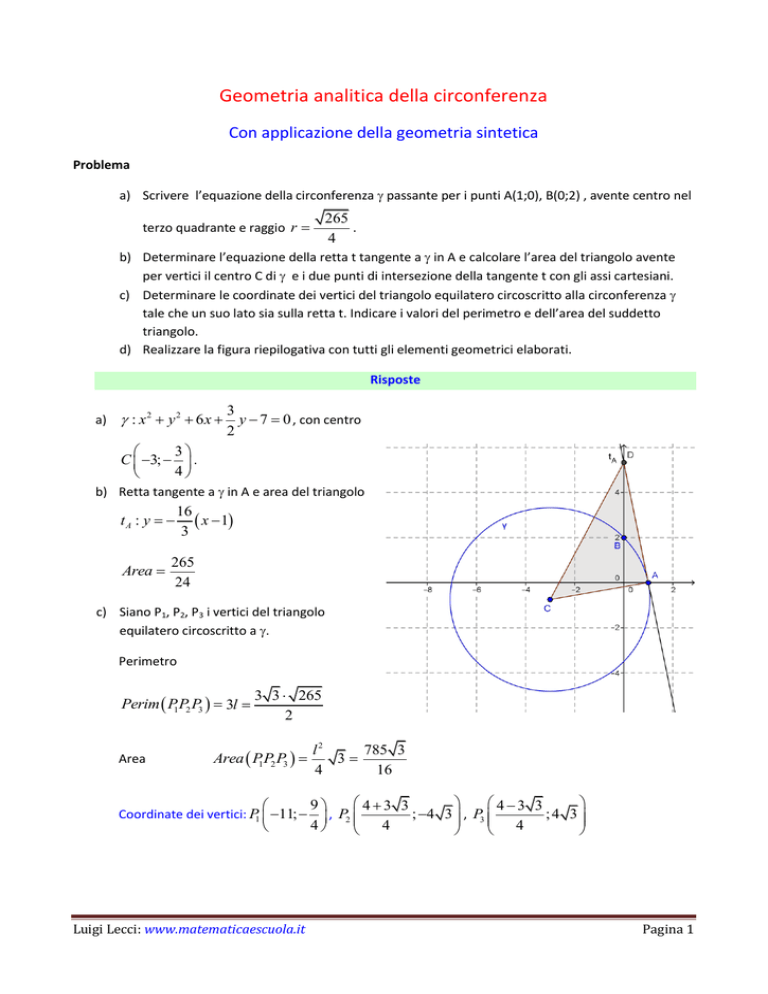
d) Realizzare la figura riepilogativa con tutti gli elementi geometrici elaborati.
Risposte
a)  : x 2  y 2  6 x 
3
y  7  0 , con centro
2
3

C  3;   .
4

b) Retta tangente a  in A e area del triangolo
tA : y  
Area 
16
 x  1
3
265
24
c) Siano P1, P2, P3 i vertici del triangolo
equilatero circoscritto a .
Perimetro
Perim  PP
1 2 P3   3l 
Area
3 3  265
2
Area  PP
1 2 P3  

l2
785 3
3
4
16
9
 43 3

 43 3

; 4 3  , P3 
; 4 3 
 4

 4

Coordinate dei vertici: P1  11;   , P2 

4

Luigi Lecci: www.matematicaescuola.it
Pagina 1