Chimica generale ed Inorganica Corso di Laurea in Chimica e

Chimica generale ed Inorganica
Corso di Laurea in
Chimica e Tecnologia Farmaceutiche (M-Z)
•
•
•
•
•
Docente: Prof. Maurizio Speranza, Prof.ssa Simonetta Fornarini
Sede: Aula Magna
Orario: Martedi (11-13), Mercoledi (9-11), Giovedi (14-16)
Spiegazioni supplementari: Studio 008, Martedi (9-11), Mercoledi (11-13)
Esercitazioni Numeriche (Dr.ssa C. Fraschetti):
Lunedì (11-13, ex-Ing), Giovedi (14-16, Magna), e Venerdi (15-17, ex-Ing),
Testi consigliati:
M. Speranza et al.: Chimica Generale ed Inorganica (edi.ermes Ed.)
J. C. Klots et al.: Chimica (Edises Ed.)
F. Cacace, M. Schiavello: Stechiometria (La Sapienza Ed.)
Esame
3 sessioni per A.A.
invernale (2 appelli), estiva (2 appelli), autunnale (1 appello)
Prova Orale
Prova Orale
<15/30 da sostenere entro 3 appelli
≥15/30
Prova Scritta
da sostenere entro 3 appelli
dalla prova scritta
3 esercizi numerici
dalla prova scritta
1 esercizio numerico
scheda +domande
scheda + domande
>18/30
<18/30
Rinuncia
<18/30
>18/30
Respinto sul libretto
La Chimica come valore
• Il signor X fa un giro in
macchina con la fidanzata !
La Chimica come valore
• Se non esistesse la
chimica della
combustione
• Se non esistesse
l’elettrochimica
La Chimica come valore
• Se non esistesse la
chimica del petrolio
• Se non esistesse la
vulcanizzazione della
gomma
La Chimica come valore
• Se non esistesse la
chimica del vetro
La Chimica come valore
• Se non esistesse la
chimica dei coloranti
La Chimica come valore
• Se non esistesse la
chimica dei polimeri
• Se non esistesse la
chimica della concia
La Chimica come valore
• Se non esistesse la
metallurgia
La Chimica come valore
• Se non esistessero le
trasformazioni
biochimiche
60000
50000
acqua
carbonio
azoto
calcio
fosforo
potassio
altri
40000
30000
20000
Non esisterebbe la vita!
10000
0
corpo umano
di 70 kg
Processo Logico Induttivo
Osservazione
del fenomeno
 Osservazione di un fenomeno
 Sua interpretazione
 Formulazione di una ipotesi
 Verifica sperimentale
 Formulazione di una teoria
Interpretazione
del fenomeno
Formulazione
di una ipotesi
Verifica
sperimentale
Formulazione
della teoria
Ipotesi
verificata ?
Verificata
più volte ?
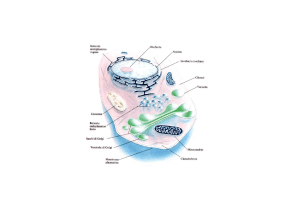
Materia
Natura della materia
Analisi elementare e strutturale
di ogni componente
Trasformazione
della materia
Separazione di
sistemi complessi
Non muta la natura
fenomeno fisico
della sostanza
fenomeno chimico
Studio dei rapporti ponderali in gioco
Studio della fattibilità di una reazione
Studio della velocità di una reazione
Muta la natura
della sostanza
STECHIOMETRIA
TERMODINAMICA
CINETICA
Proprietà della materia
Dipendenti dalle condizioni sperimentali (colore, tensione di vapore, densità, etc.)
Indipendenti dalle condizioni sperimentali (composizione, massa, etc.)
I sistemi si caratterizzano per:
-i componenti (entità chimiche con proprietà indipendenti dalla loro origine)
-le fasi (porzioni di materia che presentano le stesse proprietà in ogni loro parte)
Sistema omogeneo = una fase (uno o più componenti)
Sistema eterogeneo = più fasi (uno o più componenti)
Discriminazione fra fasi (dipende dal mezzo di osservazione; es. oro colloidale):
- occhio nudo (sistema apparentemente omogeneo)
- lente d’ingrandimento (sistema apparentemente omogeneo)
- microscopio (sistema apparentemente omogeneo)
- ultramicroscopio (sistema eterogeneo; 0.2-0.005 mm)
Stati di aggregazione della materia
Stato
gassoso
Stato
liquido
Stato
solido
• Stato gassoso
• Stato liquido
• Stato solido
Sistemi omogenei (una fase)
•
•
•
•
Miscele gassose
Soluzione (liquido in liquido)
Soluzione (solido in liquido)
Cristallo misto (solido in solido)
Sistemi eterogenei (più fasi)
•
•
•
•
•
•
•
Schiuma (gas + liquido)
Schiuma solida (gas + solido)
Nebbia (liquido + gas)
Fumo (solido + gas)
Emulsione (liquido + liquido)
Sospensione (solido + liquido)
Miscele solide (solido + solido)
Separazione dei
componenti di sistemi
eterogenei (più fasi)
•Filtrazione
•Cernita
•Flottazione
•Magnetismo
Separazione dei
componenti di sistemi
omogenei (una fase)
•Diffusione
•Distillazione
•Cristallizzazione
•Cromatografia
Separazione di sistemi complessi
ed analisi dei loro costituenti
decantazione, filtrazione, distillazione, cernita,…
trasformazioni fisiche
trasformazioni chimiche
acqua di mare
fasi solide
cristallizzazione
vapore
fasi liquide
diffusione
separazione
composto
elemento
composto
soluzione
distillazione
composto
composto
elementi
composto
elementi
elemento
Composti puri
Nome : Bromuro di Zinco
Formula : ZnBr2
Stato di aggregazione in condizioni normali : solido
Forma cristallina : cristalli rombici
Colore : nessuno
Odore : nessuno
Sapore : amaro astringente
Densità : 4.219 g/ml a 4°C
Solubilità : 447 g/100 ml acqua a 20°C
675 g/100 ml acqua a 100°C
solubile in alcool etilico ed in etere dietilico
Punto di fusione : +394°C
Punto di ebollizione : +650°C
Leggi fondamentali della chimica
Legge di Conservazione delle Masse (Lavoisier, 1789)
“La somma delle masse messe a reagire è uguale alla
somma delle masse dei prodotti di reazione”
111 mg di H si combinano con 889 mg di O per dare 1 g di H2O
1 g di N si lega con 1,142 g di O per dare 2.142 g di NO
«Alla folla è bastato un solo istante per tagliare la sua testa; ma alla Francia potrebbe non bastare un secolo per
produrne una simile» (Joseph-Louis Lagrange)
Leggi fondamentali della chimica
Legge delle Proporzioni semplici (Proust, 1799)
“Un dato composto contiene sempre gli stessi elementi nello
stesso rapporto ponderale, indipendentemente dalla sua
origine”
111 mg di H si combinano con 889 mg di O per dare 1 g di H2O
massa H/massa O = 1/8
100 g di H si combinano con 800 g di O per dare 900 g di H2O
massa H/massa O = 1/8
0.722 g di H si combinano con 5.778 g di O per dare 6.5 g di H2O
massa H/massa O = 1/8
Leggi fondamentali della chimica
Legge delle Proporzioni Multiple (Dalton, 1805)
“Quando due elementi si combinano per formare diversi
composti, le masse di un elemento che si combinano con
una data massa dell’altro stanno fra loro in rapporti che si
possono esprimere con numeri interi e semplici”
1 g di N si combina con 0.571 g di O per dare 1.571 g di N2O
1 g di N si combina con 1.142 g di O per dare 2.142 g di NO
1 g di N si combina con 2.284 g di O per dare 3.284 g di NO2
2.284 : 1.142 : 0.571 = 4 : 2: 1
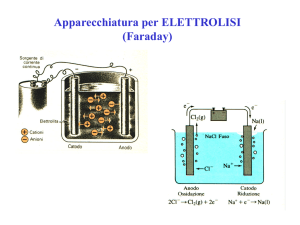
Scoperta dell’elettrone
Na+
Cl-
+
Faraday, 1834
Stoney, 1874
(M-e)+
e-
catodo anodo
deflessione verso
il polo positivo:
carica negativa ?
M Faraday
campo
elettrostatico
ombra netta del bersaglio:
fascio di particelle ?
bersaglio
metallico
W. Crookes
Esperienza di Thomson (1897)
"J.J. era piuttosto inabile manualmente e pensava di non
dover maneggiare direttamente gli strumenti. Ma egli era di
grande supporto nell’indirizzare ed organizzare gli
esperimenti dei suoi studenti”
H. F. Newall, assistente del Professor Thomson
Misura del rapporto m/e per l’elettrone
mv2/r = Hev, da cui : m/e = rH/v
campo elettrico
o magnetico
velocità v
forza agente sull’elettrone
= mv2/r
campo elettrico E
campo magnetico H
forza agente
sull’elettrone
= Ee
forza agente sull’elettrone
= Hev
Quando le due forze Ee e Hev si bilanciano : v = E/H
Misura della carica elettrica dell’elettrone
e/m = -1.76.108 Coulomb g-1 (Thomson, 1897)
radiazione ionizzante elettrone

atomizzatore di olio
N
+
-
E
telescopio
piatti del condensatore
elettricamente carichi
Massa della goccia: M
volume della goccia: V = 4pr3/3
densità dell’olio: d
accelerazione di gravità: g
catione
massa dell’elettrone (m) =
9.1.10-28
Ee
2r
g
Mg = Vdg
= 4pr3dg/3
all’equilibrio:
e = 4pr3dg/3E
Particelle elementari
Particella
Massa(g)
Carica(C)
Elettrone
Protone
Neutrone
9.106.10-28
1.6723.10-24
1.6745.10-24
-1.602.10-19
+1.602.10-19
0
Carica(e)
-1
+1
0
Raggio(m)
ca. 1.5.10-15
ca. 1.5.10-15
ca. 1.5.10-15
Numero atomico Z : numero di protoni nel nucleo (definisce l’elemento)
Numero di massa A : numero totale di protoni e neutroni nel nucleo.
Nuclide : classe omogenea di atomi tutti uguali, aventi stesso Z e A.
Nuclide :
A
60
Simbolo; es.
Co
Z
27
Gli elementi sono costituiti da uno o più nuclidi aventi lo stesso numero
atomico Z ma differente numero di massa A. Tali nuclidi si chiamano
isotopi.
Isotopi
Nuclidi con stesso Z (cioè con lo stesso numero di elettroni
nell’atomo neutro) e diverso A. Quindi, possiedono le stesse
proprietà chimiche e non possono essere separati con mezzi chimici.
11 12 13 14
C C C C
6
6 6
6
numero di atomi dell’isotopo .
abbondanza isotopica :
100
numero di atomi dell’elemento
Oltre 90 elementi con almeno un isotopo stabile
Oltre 17 elementi con tutti isotopi radioattivi
Circa 600 nuclidi stabili
Sostanze semplici conosciute da Lavoisier (1789) : Sb, As, Bi, C, Cu,
Au, H, Fe, Pb, Mn, Hg, Mo, Ni, N, O, P, Pt, Ag, S, Sn, W, Zn, CaO,
MgO, Al2O3, HCl, HF, B2O3, calore, luce. Oggi : 109 elementi.
Spettrometria di massa a tempo di volo (TOF)
elettroni veloci
rivelatore
-
+
camera di
ionizzazione
pompa da vuoto
lunghezza del tubo: L
differenza di potenziale alle estremità: V
Energia cinetica degli ioni : eV = mv2/2
Velocità degli ioni : v =  2eV/m
Tempo di volo degli ioni : t = L/v = L/  2eV/m
Tempo di volo direttamente proporzionale
alla radice quadrata della massa dello ione
Cloro naturale :
Isotopo a massa 35
Isotopo a massa 37
Difetto di massa ed energia nucleare
Difetto di massa dell’atomo 42 He
Due neutroni : 2•1.6754.10-24 g
Due protoni : 2•1.6723.10-24 g
______________________________
Totale : 6.6954.10-24 g
4
Massa del nucleo di He : 6.6461.10-24 g
2
Difetto di massa (Dm) : (6.6954-6.6461).10-24 g = 0.0513.10-24 g
Relazione di Einstein : Dm = DE/c2; DE = Dm•c2
(c: velocità della luce = 2.9979•108 m s-1)
DE = 0.0513•10-27 Kg . 8.9874•1016 m2 s-2 =
= 0.461•10-11 J = 28.77 MeV (1 MeV = 1.6022•10-15 J)
Energia nucleare
Fissione nucleare
Fusione nucleare
perchè il sole splende?
reazione netta
utilizzare la fusione per scopi bellici e pacifici
temperatura di innesco
40.000.000 °C
generare tritio da litio
Unità chimica di massa (ucm)
L’Unità Chimica di Massa (ucm) è definita come 1/12 della
massa dell’isotopo 12 del carbonio (C-12) espressa in grammi.
Massa di C-12 : 1.99252•10-23 g
Unità Chimica di Massa : 1.99252•10-23/12 g = 1.66043•10-24 g
La Massa Atomica o Peso Atomico (PA) di un nuclide è
definita come la massa del nuclide espressa in ucm.
La Massa Atomica o Peso Atomico (PA) di un elemento è definita
come la media ponderale dei PA dei nuclidi che lo compongono.
L’elemento Li è costituito da due isotopi stabili: Li-6 (PA=6.01497
ucm; 7.39%)) e Li-7 (PA=7.01590 ucm; 92.61%).
Il PA del Li è pari alla media ponderale dei PA dei suoi isotopi:
PA(Li) = 7.39•6.01497 + 92.61•7.01590= 6.940
100
Grammoatomo e Numero di Avogadro
Un grammoatomo (g-atomo) di un elemento è
definito come la massa dell’elemento pari al suo
PA espresso in grammi (es. 1 g-atomo di H (PA
1.008) = 1.008 g; 1 g-atomo di Hg (PA 200.6) =
200.6 g; 1 g-atomo di U (PA 238.06) = 238.06 g).
Quanti atomi (N) sono contenuti
in 1 g-atomo di un elemento ?
N=
1.008
23 atomi
N(H) =
=
6.023•10
1.008•1.66043.10-24
200.6
23 atomi
N(Hg) =
=
6.023•10
200.6•1.66043.10-24
238.06
23 atomi
N(U) =
=
6.023•10
238.06•1.66043.10-24
peso di 1 g-atomo
peso di 1 atomo
L’atomo secondo Thomson (1910)
Modello a “panettone”
elettroni
cariche
positive
disperse
processo di
ionizzazione
conduzione elettrica
ca. 1 Å
Struttura atomica – Raggi alfa
b
g
scatola
di piombo
campione di
U, Th, o Po
a
foglio di carta
lamina di Al
Proprietà delle particelle a (4He+2) :
-molto più massive dell’elettrone;
-cariche positivamente;
-impressionano pellicole fotografiche
Esperienza di Rutherford (1911)
lamina di Au (0.4 m)
Rutherford
Geiger
Mardsen
risultato aspettato
risultato ottenuto
particelle a
energetiche
(20000-30000 km/s)
pellicola fotografica circolare
Tracce dovute
a particelle a
rinculanti
Rutherford : “E’ stato l’avvenimento più incredibile capitatomi in tutta la mia esistenza.
Era come se avessimo sparato una cannonata contro un foglio di carta a quella ci fosse
rimbalzata addosso !”
Modelli atomici
L’atomo di Thomson: massa e carica
distribuite diffusamente nell’intero
volume dell’atomo
L’atomo di Rutherford:massa e carica
positiva concentrate nel nucleo; carica
negativa (elettroni) vagante nello
spazio circostante il nucleo.
particella a
rinculante
1 Angstrom
Antenna radio
10-4 Angstrom
tempo di vita :
ca. 10-10 s
Radiazioni elettromagnetiche
lunghezza d’onda l
ampiezza dell’onda
Profilo schematizzato di un’onda di mare in sezione
livello dell’acqua
di mare in quiete
Velocità della radiazione (v) : spazio percorso da una cresta nel tempo t
Frequenza (n) : numero di creste (n) che passano per un punto P nel tempo t
n = n/t = t’-1 ( prendendo t’ = t/n = tempo necessario per il transito di un’onda)
v = l/t’ =ln
n = v/l
variazione del
campo elettrico
carica vibrante
campo elettrico oscillante
distanza
dalla carica
vibrante
Radiazioni elettromagnetiche
variazioni del
campo elettrico
onda
elettromagnetica
variazioni del
campo magnetico
2.9977•108
distanza
dalla carica
vibrante
c = nl
n = c/l
c=
m/s (nel vuoto) (costante universale)
E = hn = hc/l (Planck, 1900) (h = 6.6262•10-34 Js (costante di Planck)
E = mc2 = hc/l (Einstein, 1905); quindi, l = h/mc
Spettri atomici
Analisi spettroscopica della luce solare
•
film
fotografico
sorgente
di luce
diaframma
Analisi spettroscopica dell’idrogeno
Gli atomi emettono
radiazioni a valori
di l discreti e non
uno spettro continuo
come la luce solare
idrogeno
gassoso
•
prisma
Spettri atomici
IR
visibile
l = 2•10-6 m;
l = 7•10-7 m;
Serie di Paschen Serie di Balmer
l = 5.9•10-7 m
l = 5.6•10-7 m
UV
l = 1.2•10-7 m;
Serie di Lyman
Raggi X (Roentgen, 1895) e Legge di Moseley
catodo
anodo
raggi X
Ka
Legge di Moseley
n(Ka) (s-1)
intensità
fascio di
elettroni
acqua di
raffreddamento
Kb
n=2.48.1015(Z-1)2
Sc
n0
E=hn
h=6.62•10-34 Js
n (cm-1)
Z2
energia degli
elettroni
intensità
di corrente
l (angstrom)
n0
n (cm-1)
Modello di Bohr (1913)
moto circolare uniforme
forza centrifuga (cinetica):
F1 = mv2/r
forza centripeta (potenziale elettrostatica):
F2 = q1q2/4per2 (e=8.85•10-12 F m-1)
Quando F1 = F2 : mv2/r = e2/r2
q1
q2 F1
elettrone
F2
nucleo
r
se la carica è espressa in ues
Bohr: “Sono stazionarie quelle orbite per le quali il momento
angolare dell’elettrone è un multiplo intero di h/2p, cioè:
mvr = nh/2p, con n = 1, 2, 3, …, 
mvr = nh/2p
v = nh/2prm
mv2/r = e2/r2
v2 = e2/mr
v2 = n2h2/4p2r2m2 = e2/mr
v2 = n2h2/4p2r2m2
mv2/2 = e2/2r
n2h2/4p2rm = e2
r = n2h2/4p2me2
En = -e2/r + e2/2r = -e2/2r = -2p2e4m/n2h2
mv2/r = q1q2/4per2 (e=8.85•10-12 F m-1) = e2/r2
carica elettrone = 4.8x10-10 ues
Modello di Bohr (1913)
r = n2h2/4p2me2
Poiché :
e = 4.8•10-10 ues
m = 9.11•10-28 g
h = 6.62•10-27 erg s
allora
[
r = 0.5292n2 (in Angstrom)
k = 2p2me4/h2 = 13.595 eV atomo-1
En = -13.595/n2 eV atomo-1
] [
1
1
DE = E2-E1 = hc/l = -k
=k
2
2
n2
n1
2n 2
3c
n
h
1 2
hc
l = hc/DE = k
= 2p2me4
2
2
n2 n1
[
n = 1, 2, 3, …, 
En = -2p2me4/n2h2 = -k/n2
]
2me4
2p
-1
RH =
=
109737.3
cm
3
hc
[
]
n22 n12
n12n22
n12n22
1
=
RH
n22 n12
]
[
n12n22
n22 n12
]
Modello di Bohr (1913)
UV(97551 cm-1)
E1/16
E1/9
En = -2p2me4/n2h2
vis(15233 cm-1)
E1/4
E1
n=4 n=3 n=2 n=1
r = n2h2/4p2me2
n = 1, 2, 3, …, 
IR(5331 cm-1)
°
r=0.53 A
DE = E2-E1 = hn
°
r=2.12 A
atomo di idrogeno
° E(eV) E(cm-1)
n r(A)
1 0.53 -13.6 -109737
2 2.12 -3.4 -27420
3 4.77 -1.5 -12186
4 8.48 -0.8
-6855
°
r=4.77 A
°
r=8.48 A
r = 0.5292n2 (in Angstrom)
En = -13.595/n2 eV atomo-1
Spettri atomici e transizioni elettroniche
n=
limite di ionizzazione
n=5
n=4
n=3
Pfund
Brackett
Paschen
Paschen
Balmer
n=2
6562.79
limite
3645.60
4101.74
4340.74
4861.33
Balmer
l in A°
n=1
[n
4
l=
109737.3
Lyman
= 3645.6
Lyman
[n
n2
2
2
n22
2
2
2
4
4
]
] A°
Modello di Sommerfield
doppietto
 Molte righe sono in realtà doppietti
 Molte righe diventano doppietti o
multipletti quando l’emissione ha
luogo in un campo elettrico (effetto
Stark) o magnetico (effetto Zeeman).
Orbita circolare (Bohr)
a=b
Orbite quantizzate
a
b
a>b

Orbita ellittica (Sommerfield)
Nucleo in uno dei due fuochi
dell’ellisse.
Eccentricità dell’ellisse : a-b
n (principale) 8 dimensioni dell’orbita
l (secondario) 8 eccentricità dell’orbita
m (magnetico) 8 effetti Stark e Zeeman
Transizioni elettroniche secondo Bohr-Sommerfield
doppietto
Effetto Stark ed effetto Zeeman
energia
n=2
E2,1
E2,0
l=1
l=0
DE = hn0
n=1
l=0
DE = hn1
E1,0
Numeri quantici
Notazione spettroscopica per i gusci
Notazione spettroscopica per i gusci
l = 0n-1
n guscio n guscio
•1
•2
•3
•4
•K
•L
•M
•N
•5
•6
•7
•O
•P
•Q
sottoguscio
•0
•1
•2
•3
•s(sharp)
•p(principal)
•d(diffuse)
•f (fundamental)
Possibili valori di m e numero di orbitali
l
m = - l + l
•0
•1
•2
•3
•0
•-1, 0, +1
•-2, -1, 0, +1, +2
•-3, -2, -1, 0, +1, +2, +3
numero di orbite
•1
•3
•5
•7
L’esperimento di Stern-Gerlach (1920)
lastra fotografica
Ag
Atomi con spin parallelo alle linee
di forza del campo magnetico
Ag
Atomi con spin antiparallelo alle
linee di forza del campo magnetico
campo magnetico disomogeneo
47Ag
“L’elettrone possiede la proprietà dello spin,
cioè si può considerare come una sfera rotante
o in senso destrorso o in senso sinistrorso”.
Numero di spin
N
N
N
S
S
S
S
N
s = +1/2
s = +1/2 s = +1/2
s = -1/2
repulsione magnetica
attrazione magnetica
N
S
N
N
S
S
S
N
Teoria dei quanti
Diffrazione di raggi X attraverso
una lamina d’alluminio
100 elettroni
Diffrazione di elettroni attraverso
una lamina d’alluminio
3000 elettroni
70000 elettroni
Onde materiali
E = hn = hc/l (Planck)
E = mc2 (Einstein)
Relazione per il fotone di Planck-Einstein : m = h/lc
Riarrangiando e generalizzando :
l = h/mv
De Broglie: “Ogni oggetto di massa m e velocità
v ha anche proprietà ondulatorie definite da una
lunghezza d’onda l ed una frequenza n”
Per oggetti pesanti, es. una pallottola di fucile con m = 25 g e v = 9•104 cm s-1:
6.6•10-27 erg s
(troppo piccola per
-33
l = h/mv =
= 2.9•10 cm avere senso fisico)
4
-1
25•9•10 g cm s
Per elettroni (m = 9.1•10-28 g e v = 3•109 cm s-1 (cioè 0.1 c)):
6.6•10-27 erg s
°
-9 cm = 0.24 A
l = h/mv =
=
2.4•10
9.1•10-28•3•109 g cm s-1
(la metà del raggio della prima orbita di Bohr)
Principio di indeterminazione di Heisenberg (1926)
E1<E2
E1=hn1
n1<n2
Grande incertezza
sulla posizione;
piccola incertezza
sul momento mv
E2=hn2
Piccola incertezza
sulla posizione;
grande incertezza
sul momento mv
“Contrariamente a quanto avviene per gli oggetti pesanti, è impossibile
determinare esattamente ad ogni istante la posizione di un elettrone e
la sua velocità” (Werner Heisenberg, 1926)
Principio di indeterminazione di Heisenberg (1926)
z
mv
r
y
x
Dr.Dmv = h/2p
Per un oggetto pesante (m=50 g)
Per l’elettrone (m=9.1•10-28 g)
Se Dr = 10-3 cm (trascurabile)
Se Dr = 0.02 A° = 2•10-10 cm
Dmv=h/2pDr
-27
-27
6.6
•
10
-24 g cm s-1
6.6
•
10
-18 g cm s-1
=
1
•
10
Dmv =
Dmv =
=
5
•
10
6.28•10-3
6.28-18•2•10-10
-24
1
•
10
5
•
10
= 2•10-26 cm s-1 (trascurabile)
Dv =
= 5•109 cm s-1
Dv =
50
-28
9.1•10(Un
sesto della velocità della luce !)
Per l’elettrone: Dr piccoloDv grande
Dr grandeDv piccolo
L’elettrone che ruota su un’orbita
stazionaria è incompatibile col
principio di Heisenberg
Fenomeni di interferenza delle onde elettromagnetiche
schermo
Le onde si propagano a ventaglio
quando fuoriescono da un orifizio
in fase
fuori fase
diaframma con due orifizi
Onde stazionarie
Nelle onde progressive, la posizione dei ventri
Nelle onde stazionarie, la posizione
e dei nodi si sposta nel tempo e si ha trasporto
dei ventri e dei nodi è costante nel
tempo e non si ha trasporto di energia. di energia.


 
Onde stazionarie
l
l*
r
r
Affinchè l’onda non si autodistrugga (onda stazionaria),
la sua lunghezza d’onda l deve essere un sottomultiplo
della circonferenza, cioè nl =2pr (n=1,2,3,…).
2pr = n
l
Sono possibili infinite onde stazionarie.
Modello quantistico dell’atomo di idrogeno
Condizione di stazionarietà :
Relazione di De Broglie :
2pr
l= n
h
l = mv
Relazione di Bohr
nh
mvr =
2p
“L’esistenza delle orbite di Bohr discende come
conseguenza necessaria del carattere ondulatorio dell’elettrone”
L’elettrone che ruota intorno al nucleo è
incompatibile col
v
principio di
r0
indeterminazione
e con l’elettrodinamica
classica (l’elettrone dovrebbe
emettere radiazioni e cadere sul nucleo.
L’elettrone non ruota. E’ un’onda
stazionaria che segue la
condizione di Bohr. La
posizione dell’elettrone
non è definita. Solo la
probabilità di trovare
l’elettrone è massima a r0.
Equazione di Schrodinger (1926)
Hy = Ey
operatore Hamiltoniano
2
2 2
e
h
H= 2
r
8p m
(
)
La funzione y non ha significato fisico, ma il suo
quadrato y2 esprime la probabilità di trovare l’elettrone
in un volume unitario centrato nel punto P.
z
Soluzioni significative di y solo se
obbediscono alla condizione di stazionarietà
(autovalori). Per ciascun autovalore, esistono
infinite soluzioni che soddisfano criteri di
univocità, continuità, e normalizzazione
(autofunzioni o funzioni d’onda)
Normalizzazione
y2

-
+
Y2dt = 1
-
P
x
O
y
nucleo
Univocità
univoca
volume unitario
non univoca
Continuità
y2
continua
discontinua
Funzioni d’onda per l’idrogeno e per gli atomi idrogenoidi
2m
2
8p
e
2
+
(E )y = 0
y
2
r
h
Autovalori per
Condizione di stazionarietà
En = -2p2me4/n2h2
n ≥0
l ≤ n-1 (interi positivi)
-l < m < +l
z
(Bohr)
parte
parte
radiale angolare y
Orbitale
s
p
d
f
q
r
Ynlm = Rnl(r) . Alm(q, j)
Parte Radiale
+
+
+
+
Parte Angolare
+
+
+
j
Carattere
adirezionale
direzionale
direzionale
direzionale
x
Densità di probabilità e probabilità radiale
y2
n =1
l =0
m=0
Orbitale 1s
r
r n=1, l=0, m=0
densità di probabilità
centrosimmetrico
4pr2 y2
Il numero di
volumetti unitari
(dV) che sono
posti alla distanza
r dal centro è
espresso da 4pr2.
y2
4pr2
r
r0=0.53 angstrom
probabilità radiale
r
Orbitali atomici
y2
n = 2; l = 0; m = 0
Orbitale 2s
r
densità di probabilità
4pr2 y2
2
4pr
y2
r
piano nodale
probabilità radiale
n=2, l=0, m=0
centrosimmetrico
Orbitali atomici
z
z
y
y
y
x
x
x
z
Orbitale 2pz
Orbitale 2py
n=2, l=1, m=-1
orientato lungo
l’asse z
piano nodale xy
n=2, l=1, m=0
orientato lungo
l’asse y
piano nodale xz
Orbitale 2px
n=2, l=1, m=+1
orientato lungo
l’asse x
piano nodale yz
Orbitali atomici
n=3, l=2,
m=-2; -1; 0; +1; +2
z
z
Orbitale
Orbitale3d3dx2x-y2-y
2 2
x
Orbitale 3dxy
y
y
x
z
z
Orbitale 3dxz
y
x
y
z
Orbitale 3dyz
x
x
Orbitale 3dz2
y
Orbitali atomici
m=0
n=1
l=0
n=2
l=0
n=2
l=1
n=3
l=0
n=3
l=1
n=3
l=2
m=1
m=2
m=3
Orbitali atomici
m=0
n=4
l=0
n=4
l=1
n=4
l=2
n=4
l=3
m=1
m=2
m=3
Orbitali atomici
n l
ml
Sotto
gruppo
Numero degli orbitali
nel sottogruppo
1 0
2 0
0
0
1s
2s
1
1
1
0
1
2
-1, 0, +1
0
-1, 0, +1
-2, -1, 0, +1, +2
2p
3s
3p
3d
3
1
3
5
4 0
4 1
4 2
0
-1, 0, +1
-2, -1, 0, +1, +2
4s
4p
4d
1
3
5
4f
7
2
3
3
3
4 3 -3, -2, -1, 0, +1, +2, +3
Energia degli orbitali atomici
Energia
4s
3s
4p
3p
4d
3d
4f
4s
3s
3d
3p
2p
2s 2p
1s
2s
1s
Energia degli orbitali atomici
E
3s
3p
3d
3d
3p
3s
2s
2p
2p
2s
1s
4p
1s
H
He
4d
3d
4s
elementi di
elementi di
pre-transizione transizione
4s
3d
3s
3p
3s
2p
2s
2p
2s
1s
Ne
Ca
1s
4s
numero atomico Z
4p
3p
3d
En = -
Sc
2p2Z2e4m
n2h2
Energia degli orbitali
atomici in funzione del
numero atomico Z
7
Numero quantico principale n
6
5
7p
7s
4
6s
3
5s
6d
6p
5p
5d
4f
4p
2
4d
4s
1
3s
2s
1s
Numero atomico Z
5f
3p
2p
3d
Costruzione (“aufbau”) della configurazione elettronica di un
atomo
Principio di esclusione (Pauli, 1925)
Gli elettroni di un atomo non possono essere
caratterizzati dagli stessi numeri quantici
Principio di minima energia
Gli elettroni tendono a collocarsi negli
orbitali disponibili a più bassa energia
Principio di massima molteplicità (Hund, 1925)
Gli elettroni tendono a collocarsi con spin
parallelo nel massimo di orbitali degeneri disponibili
Configurazione elettronica degli elementi
atomo
Z
•H
•He
•Li
•Be
•B
•C
•N
•O
•F
•Ne
•Na
•1
•2
•3
•4
•5
•6
•7
•8
•9
•10
•11
configurazione elettronica nello stato fondamentale
•1s1
•1s2
•1s2 2s1
•1s2 2s2
•1s2 2s2 2p1
•1s2 2s2 2p2
•1s2 2s2 2p3
•1s2 2s2 2p4
•1s2 2s2 2p5
•1s2 2s2 2p6
•1s2 2s2 2p6 3s1
3d
3p
o
He
He
3s
He
2s
2p
He
He
1s
He
He
He
He
o
Ne
Eccezioni al principio Aufbau (i sottogruppi d ed f semioccupati o
completamente occupati godono di extra-stabilità), es.:
•Cr
•Cu
configurazione Aufbau
•1s2 2s2 2p6 3s2 3p6 3d4 4s2
•1s2 2s2 2p6 3s2 3p6 3d9 4s2
configurazione reale
•1s2 2s2 2p6 3s2 3p6 3d5 4s1
•1s2 2s2 2p6 3s2 3p6 3d10 4s1
Configurazione elettronica degli elementi
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
simbolo
H
He
Li
Be
B
C
N
O
F
Ne
Na
Mg
Al
Si
P
S
Cl
Ar
atomo neutro
1s1
1s2
[He] 2s1
[He] 2s2
[He] 2s2 2p1
[He] 2s2 2p2
[He] 2s2 2p3
[He] 2s2 2p4
[He] 2s2 2p5
[He] 2s2 2p6
[Ne] 3s1
[Ne] 3s2
[Ne] 3s2 3p1
[Ne] 3s2 3p2
[Ne] 3s2 3p3
[Ne] 3s2 3p4
[Ne] 3s2 3p5
[Ne] 3s2 3p6
catione
–
1s1
1s2
[He] 2s1
[He] 2s2
[He] 2s2 2p1
[He] 2s2 2p2
[He] 2s2 2p3
[He] 2s2 2p4
[He] 2s2 2p5
[He] 2s2 2p6
[Ne] 3s1
[Ne] 3s2
[Ne] 3s2 3p1
[Ne] 3s2 3p2
[Ne] 3s2 3p3
[Ne] 3s2 3p4
[Ne] 3s2 3p5
Configurazione elettronica degli elementi
Z
simbolo
19
K
20
Ca
21
Sc
22
Ti
23
V
24
Cr
25
Mn
1°
tr.
26
Fe
27
Co
28
Ni
29
Cu
30
Zn
31
Ga
32
Ge
33
As
34
Se
35
Br
36
Kr
atomo neutro
[Ar] 4s1
[Ar] 4s2
[Ar] 3d1 4s2
[Ar] 3d2 4s2
[Ar] 3d3 4s2
[Ar] 3d5 4s1
[Ar] 3d5 4s2
[Ar] 3d6 4s2
[Ar] 3d7 4s2
[Ar] 3d8 4s2
[Ar] 3d10 4s1
[Ar] 3d10 4s2
[Ar] 3d10 4s2 4p1
[Ar] 3d10 4s2 4p2
[Ar] 3d10 4s2 4p3
[Ar] 3d10 4s2 4p4
[Ar] 3d10 4s2 4p5
[Ar] 3d10 4s2 4p6
4s
4s
3s
2s
1s
[Ne] 3s2 3p6
[Ar] 4s1
[Ar] 3d1 4s1
[Ar] 3d2 4s1
[Ar] 3d4
3d 5
[Ar] 3d
3d
3p
[Ar] 3d5 4s1
catione
[Ar] 3d6 4s1
2p
[Ar] 3d8
[Ar] 3d9
[Ar] 3d10
Ne
Ca1
Ca
Zn
10
[Ar] 3d 4s
[Ar] 3d10 4s2
[Ar] 3d10 4s2 4p1
[Ar] 3d10 4s2 4p2
[Ar] 3d10 4s2 4p3
[Ar] 3d10 4s2 4p4
[Ar] 3d10 4s2 4p5
Configurazione elettronica degli elementi
Z
simbolo
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
Pd
Ag
Cd
In
Sn
Sb
Te
I
Xe
2° tr.
atomo neutro
[Kr] 5s1
[Kr] 5s2
[Kr] 4d1 5s2
[Kr] 4d2 5s2
[Kr] 4d4 5s1
[Kr] 4d5 5s1
[Kr] 4d5 5s2
[Kr] 4d7 5s1
[Kr] 4d8 5s1
[Kr] 4d10
[Kr] 4d10 5s1
[Kr] 4d10 5s2
[Kr] 4d10 5s2 5p1
[Kr] 4d10 5s2 5p2
[Kr] 4d10 5s2 5p3
[Kr] 4d10 5s2 5p4
[Kr] 4d10 5s2 5p5
[Kr] 4d10 5s2 5p6
catione
5p
5s
4p
4s
3p
3s
2p
2s
1s
[Ar] 3d10 4s2 4p6
[Kr] 5s1
[Kr] 5s2
[Kr] 4d2 5s1
[Kr] 4d4
4f
[Kr] 4d5
5
1
[Kr]
4d 4d 5s
[Kr] 4d7
3d 4d8
[Kr]
[Kr] 4d9
[Kr] 4d10
[Kr] 4d10 5s1
[Kr] 4d10 5s2
[Kr] 4d10 5s2 5p1
[Kr] 4d10 5s2 5p2
[Kr] 4d10 5s2 5p3
[Kr] 4d10 5s2 5p4
[Kr] 4d10 5s2 5p5
Configurazione elettronica degli elementi
Z
simbolo
lantanidi
55
56
57 3° tr.
58
59
60
61
62
63
64
65
66
67
68
69
70
71
Cs
Ba
La
Ce
Pr
Nd
Pm
Sm
Eu
Gd
Tb
Dy
Ho
Er
Tm
Yb
Lu
atomo neutro
[Xe] 6s1
[Xe] 6s2
[Xe] 5d1 6s2
[Xe] 4f1 5d1 6s2
[Xe] 4f3 6s2
[Xe] 4f4 6s2
[Xe] 4f5 6s2
[Xe] 4f6 6s2
[Xe] 4f7 6s2
[Xe] 4f7 5d1 6s2
[Xe] 4f9 6s2
[Xe] 4f10 6s2
[Xe] 4f11 6s2
[Xe] 4f12 6s2
[Xe] 4f13 6s2
[Xe] 4f14 6s2
[Xe] 4f14 5d1 6s2
catione
6p
6s
5p
5s
4p
4s
3p
3s
2p
2s
1s
[Kr] 4d10 5s2 5p6
[Xe] 6s1
[Xe] 5d2
[Xe] 4f1 5d2
[Xe] 4f3 6s1
5d
[Xe]
4f4 6s1 4f
[Xe] 4f5 6s1
4d
[Xe] 4f6 6s1
7
1
[Xe]
3d 4f 6s
[Xe] 4f7 5d1 6s1
[Xe] 4f9 6s1
[Xe] 4f10 6s1
[Xe] 4f11 6s1
[Xe] 4f12 6s1
[Xe] 4f13 6s1
[Xe] 4f14 6s1
[Xe] 4f14 6s2
Configurazione elettronica degli elementi
Z
simbolo
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
Hf
Ta
W
Re
Os
Ir
Pt
Au
Hg
Tl
Pb
Bi
Po
At
Rn
3° tr.
atomo neutro
[Xe] 4f14 5d2 6s2
[Xe] 4f14 5d3 6s2
[Xe] 4f14 5d4 6s2
[Xe] 4f14 5d5 6s2
[Xe] 4f14 5d6 6s2
[Xe] 4f14 5d7 6s2
[Xe] 4f14 5d9 6s1
[Xe] 4f14 5d10 6s1
[Xe] 4f14 5d10 6s2
[Xe] 4f14 5d10 6s2 6p1
[Xe] 4f14 5d10 6s2 6p2
[Xe] 4f14 5d10 6s2 6p3
[Xe] 4f14 5d10 6s2 6p4
[Xe] 4f14 5d10 6s2 6p5
[Xe] 4f14 5d10 6s2 6p6
catione
[Xe] 4f14 5d1 6s2
[Xe] 4f14 5d3 6s1
[Xe] 4f14 5d4 6s1
[Xe] 4f14 5d5 6s1
[Xe] 4f14 5d6 6s1
[Xe] 4f14 5d7 6s1
[Xe] 4f14 5d9
[Xe] 4f14 5d10
[Xe] 4f14 5d10 6s1
[Xe] 4f14 5d10 6s2
[Xe] 4f14 5d10 6s2 6p1
[Xe] 4f14 5d10 6s2 6p2
[Xe] 4f14 5d10 6s2 6p3
[Xe] 4f14 5d10 6s2 6p4
[Xe] 4f14 5d10 6s2 6p5
Configurazione elettronica degli elementi
4° tr.
attinidi
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
simbolo
Fr
Ra
Ac
Th
Pa
U
Np
Pu
Am
Cm
Bk
Cf
Es
Fm
Md
No
Lr
atomo neutro
[Rn] 7s1
[Rn] 7s2
[Rn] 6d1 7s2
[Rn] 6d2 7s2
[Rn] 5f2 6d1 7s2
[Rn] 5f3 6d1 7s2
[Rn] 5f4 6d1 7s2
[Rn] 5f5 6d1 7s2
[Rn] 5f6 6d1 7s2
[Rn] 5f7 6d1 7s2
[Rn] 5f8 6d1 7s2
[Rn] 5f9 6d1 7s2
[Rn] 5f10 6d1 7s2
[Rn] 5f11 6d1 7s2
[Rn] 5f12 6d1 7s2
[Rn] 5f13 6d1 7s2
[Rn] 5f14 6d1 7s2
catione
transuranici
(artificiali)
Z
[Xe] 4f14 5d10 6s2 6p6
[Rn] 7s1
[Rn] 7s2
[Rn] 6d2 7s1
[Rn] 5f2 7s2
[Rn] 5f3 7s2
[Rn] 5f4 7s2
[Rn] 5f5 7s2
[Rn] 5f6 7s2
[Rn] 5f7 7s2
[Rn] 5f8 7s2
[Rn] 5f9 7s2
[Rn] 5f10 7s2
[Rn] 5f11 7s2
[Rn] 5f12 7s2
[Rn] 5f13 7s2
[Rn] 5f14 7s2 Glenn Seaborg
Sintesi di nuovi elementi artificiali
1952
   
   
   
1953
1955
99Es
100Fm
1960
1968
103Lw
104Rf
101Md
102No
1973
1969
105Db
1984
1982
1958
106Sg
1997
1980
107Bh
109Hs
108Mt
110Uun
Periodicità delle configurazioni elettroniche
Z
1
3
11
19
37
55
87
simbolo
H
Li
Na
K
Rb
Cs
Fr
configurazione
1s1
[He] 2s1
[Ne] 3s1
[Ar] 4s1
[Kr] 5s1
[Xe] 6s1
[Rn] 7s1
periodo
1°
2°
3°
4°
5°
6°
7°
Z
2
4
12
20
38
56
88
simbolo
He
Be
Mg
Ca
Sr
Ba
Ra
configurazione
1s2
[He] 2s2
[Ne] 3s2
[Ar] 4s2
[Kr] 5s2
[Xe] 6s2
[Rn] 7s2
periodo
1°
2°
3°
4°
5°
6°
7°
Periodicità delle configurazioni elettroniche
Z
5
13
31
49
81
simbolo
B
Al
Ga
In
Tl
configurazione
periodo
[He] 2s2 2p1
2°
[Ne] 3s2 3p1
3°
[Ar] 3d10 4s2 4p1
4°
[Kr] 4d10 5s2 5p1
5°
[Xe] 4f14 5d10 6s2 6p1
6°
Z
6
14
32
50
82
simbolo
C
Si
Ge
Sn
Pb
configurazione
periodo
[He] 2s2 2p2
2°
[Ne] 3s2 3p2
3°
[Ar] 3d10 4s2 4p2
4°
[Kr] 4d10 5s2 5p2
5°
[Xe] 4f14 5d10 6s2 6p2
6°
Periodicità delle configurazioni elettroniche
Z
7
15
33
51
83
simbolo
N
P
As
Sb
Bi
configurazione
periodo
[He] 2s2 2p3
2°
[Ne] 3s2 3p3
3°
[Ar] 3d10 4s2 4p3
4°
[Kr] 4d10 5s2 5p3
5°
[Xe] 4f14 5d10 6s2 6p3
6°
Z
8
16
34
52
84
simbolo
O
S
Se
Te
Po
configurazione
periodo
[He] 2s2 2p4
2°
[Ne] 3s2 3p4
3°
[Ar] 3d10 4s2 4p4
4°
[Kr] 4d10 5s2 5p4
5°
[Xe] 4f14 5d10 6s2 6p4
6°
Periodicità delle configurazioni elettroniche
Z
9
17
35
53
85
simbolo
F
Cl
Br
I
At
configurazione
periodo
[He] 2s2 2p5
2°
[Ne] 3s2 3p5
3°
[Ar] 3d10 4s2 4p5
4°
[Kr] 4d10 5s2 5p5
5°
[Xe] 4f14 5d10 6s2 6p5
6°
Z
simbolo
configurazione
2
10
18
36
54
86
He
Ne
Ar
Kr
Xe
Rn
1s2
[He] 2s2 2p6
[Ne] 3s2 3p6
[Ar] 3d10 4s2 4p6
[Kr] 4d10 5s2 5p6
[Xe] 4f14 5d10 6s2 6p6
periodo
1°
2°
3°
4°
5°
6°
Periodicità delle configurazioni elettroniche
Z
5
13
31
49
81
simbolo
B
Al
Ga
In
Tl
configurazione
periodo
[He] 2s2 2p1
2°
[Ne] 3s2 3p1
3°
[Ar] 3d10 4s2 4p1
4°
[Kr] 4d10 5s2 5p1
5°
[Xe] 4f14 5d10 6s2 6p1
6°
Z
21
39
57
89
simbolo
Sc
Y
La
Ac
configurazione
[Ar] 3d1 4s2
[Kr] 4d1 5s2
[Xe] 5d1 6s2
[Rn] 6d1 7s2
periodo
4°
5°
6°
7°
Periodicità delle configurazioni elettroniche
Z
22
40
72
simbolo
Ti
Zr
Hf
configurazione
[Ar] 3d2 4s2
[Kr] 4d2 5s2
[Xe] 4f14 5d2 6s2
periodo
4°
5°
6°
Z
23
41
73
simbolo
V
Nb
Ta
configurazione
[Ar] 3d3 4s2
[Kr] 4d4 5s1
[Xe] 4f14 5d3 6s2
periodo
4°
5°
6°
Z
24
42
74
simbolo
Cr
Mo
W
configurazione
[Ar] 3d5 4s1
[Kr] 4d5 5s1
[Xe] 4f14 5d4 6s2
periodo
4°
5°
6°
Periodicità delle configurazioni elettroniche
Z
25
43
75
simbolo
Mn
Tc
Re
configurazione
[Ar] 3d5 4s2
[Kr] 4d5 5s2
[Xe] 4f14 5d5 6s2
periodo
4°
5°
6°
Z
26
44
76
simbolo
Fe
Ru
Os
configurazione
[Ar] 3d6 4s2
[Kr] 4d7 5s1
[Xe] 4f14 5d6 6s2
periodo
4°
5°
6°
27
45
77
Co
Rh
Ir
[Ar] 3d7 4s2
[Kr] 4d8 5s1
[Xe] 4f14 5d7 6s2
4°
5°
6°
28
46
78
Ni
Pd
Pt
[Ar] 3d8 4s2
[Kr] 4d10
[Xe] 4f14 5d9 6s1
4°
5°
6°
Periodicità delle configurazioni elettroniche
Z
1
3
11
19
37
55
87
simbolo
H
Li
Na
K
Rb
Cs
Fr
configurazione
1s1
[He] 2s1
[Ne] 3s1
[Ar] 4s1
[Kr] 5s1
[Xe] 6s1
[Rn] 7s1
periodo
1°
2°
3°
4°
5°
6°
7°
Z
29
47
79
simbolo
Cu
Ag
Au
configurazione
[Ar] 3d10 4s1
[Kr] 4d10 5s1
[Xe] 4f14 5d10 6s1
periodo
4°
5°
6°
Periodicità delle configurazioni elettroniche
Z
2
4
12
20
38
56
88
simbolo
He
Be
Mg
Ca
Sr
Ba
Ra
configurazione
1s2
[He] 2s2
[Ne] 3s2
[Ar] 4s2
[Kr] 5s2
[Xe] 6s2
[Rn] 7s2
periodo
1°
2°
3°
4°
5°
6°
7°
Z
30
48
80
simbolo
Zn
Cd
Hg
configurazione
[Ar] 3d10 4s2
[Kr] 4d10 5s2
[Xe] 4f14 5d10 6s2
periodo
4°
5°
6°
Tavola periodica
Tavola periodica
4° gruppo
2° gruppo
5° gruppo
3° gruppo
B
C
N
10.81
12.01
14.01
Mg
Al
Si
P
24.31
26.98
28.09
30.97
Zn
?
As
65.37
?
74.92
Cd
In
Sn
Sb
112.41
114.82
118.69
121.75
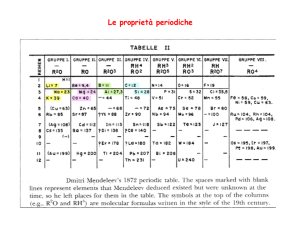
Elementi sconosciuti:
Dmitri Mendeleev (1869)
2° periodo
3° periodo
4° periodo
5° periodo
ekaalluminio ekasilicio
ekasilicio
Caratteristiche
... previste nel 1871
Colore
Peso Atomico
Densità (g/ml)
Calore Specifico (J/gK)
Formula dell'ossido
Densità ossido (g/ml)
Formula del cloruro
Densità cloruro (g/ml)
grigio
72
5.5
0.31
XO2
4.7
XCl4
1.9
... e riscontrate nel 1886
bianco-grigiastro
72.59
5.35
0.31
GeO2
4.70
GeCl4
1.84
Raggi Atomici
Periodicità dei raggi atomici
Periodicità delle energie di ionizzazione
He
H
Energie di
ionizzazione (eV)
100
Be
B
Li
O
C
Ne
F
N
Mg
Na
S
Si
Al
P
Ar
Cl
75
50
III° ionizz.
II° ionizz.
25
I° ionizz.
0
0
2
4
6
8
10 12 14 16 18 20
Numero atomico (N)
Periodicità delle energie di ionizzazione
Periodicità delle affinità elettroniche
Affinità elettronica (eV)
4
Cl
F
3
2
Si
C
H
1
S
O
Li
Na
P
0
Al
B
Be
N
Mg
He
-1
Ar
Ne
-2
0
2
4
6
8
10
12
14
Numero atomico (N)
16
18
Molecole ed aggregati ionici
Molecole: aggregati atomici stabili che
costituiscono entità discrete, con un
numero preciso di atomi costituenti.
Formule molecolari: H2O, I2, C2H4O, etc.
Cristallo ionico: aggregato di ioni positivi e
negativi, in cui gli ioni non costituiscono entità
discrete, ma interagiscono elettrostaticamente
con tutti gli ioni circostanti. Non si possono quindi
identificare entità molecolari, ma tutto il cristallo
costituisce un macroaggregato.
Formula minima: NaCl, MgI2, ZnO, etc. (definisce il rapporto
numerico fra cationi ed anioni).
Peso molecolare, peso formula, e mole.
Unità chimica di massa (ucm): 1/12 della massa del 12C6.
Massa atomica (PA): massa di un atomo espressa in ucm.
Massa molecolare (PM): massa di una molecola espressa in ucm.
Massa formula (PF): somma dei PA dei componenti una formula minima.
PM = Si ci(PA)i (ci = indice numerico dell’atomo i-esimo)
Es.: glucosio C6H12O6
PM (glucosio) = 6•12.00 + 12•1.008 + 6•15.999 = 180.09
Grammoatomo: grammi di un elemento pari al suo PA.
Grammomolecola o mole: grammi di un composto pari al suo PM.
Grammoformula o mole: grammi di un composto ionico pari al suo PF.
Mole: un numero di Avogadro (N = 6.023•1023) di oggetti uguali
(atomi, elettroni, molecole, neutroni, ioni, automobili, batteri, etc.)
Valenza: numero di legami con atomi
di idrogeno che un atomo può formare
Li, Na, K, … (I° gruppo) : monovalenti
Mg, Ca, Ba, … (II° gruppo) : bivalenti
B, Al, … (III° gruppo) : trivalenti
C, Si, Ge, … (IV° gruppo) : tetravalenti
N (V° gruppo) : trivalente
O (VI° gruppo) : bivalente
F (VII° gruppo) : monovalente
Formule Chimiche
Formule Molecolari : C2H4O
Formule Minime : NaCl
HH
Formule di Struttura :
H-C-C=O
H
HH
Isomeria :
H
H-C-C=O
H
H-C
acetaldeide
C-H ossido di
O
etilene
O
H
N-N
H
H
O nitrammide
HO-N=N-OH acido
iponitroso
Regola dell’Ottetto (Kossel e Lewis, 1916)
Configurazione elettronica ad ottetto dei gas nobili :
Ne : (He) s2p6
Ar : (Ne) s2p6
Kr : (Ar) s2p6
Xe : (Kr) s2p6
Gli elementi tendono a conseguire la configurazione
elettronica stabile ad ottetto dei gas nobili.
+
Legame ionico :
donatore
accettore
elettrone
Legame covalente :
2 elettroni
Legame dativo :
donatore
2 elettroni
messa a comune di elettroni
accettore
Alcuni elementi possono anche espandere l’ottetto e conseguire
una configurazione con 12 elettroni (es.: S in SF6).
Altri possono conseguire un configurazione stabile a d5 (es.: Mn+2).
Energia e distanza di legame
Legame
H-H
H-F
H-Cl
H-Br
H-I
O=O
N≡N
Legame
C-C
C=C
C≡C
C∸C
Energia
(eV/legame)
4.51
5.85
4.47
3.82
3.08
5.16
9.76
Energia
(kcal/mole)
104
135
103
88
71
119
225
Distanza
(Å)
0.75
0.92
1.27
1.41
1.61
1.20
1.09
Sostanza
Energia
(kcal/mole)
83.2
146.8
200.6
140.2
Distanza
(Å)
1.54
1.34
1.20
1.39
C2H6
C2H4
C2H2
C6H6
Legame Ionico
Legame elettrostatico adirezionale che si
stabilisce fra un elemento metallico (Na)
ed uno non metallico (Cl).
Na=1s22s22p63s1
Cl=1s22s22p63s23p5
Na(gas) → Na+(gas) + e; costa 5.14 eV
Cl(gas) + e → Cl-(gas); guadagna 3.71 eV
forza di attrazione elettrostatica: F=
k=8.99x109 Jm/C2
energia potenziale elettrostatica: U=
costa 1.43 eV
kQ1Q2
r2
kQ1Q2
r
=-
kZ1Z2e2
r
L’energia U decresce fino alla distanza di equilibrio, dove le
forze attrattive sono bilanciate da quelle repulsive dovute alla
sovrapposizione delle nuvole elettroniche dei due ioni.
Legame Ionico
+U
Per NaCl : r0=2.36 Å
A questa distanza:
-
+
kZ1Z2e2
ke2
== -6.12 eV
U= r0
r0
potenziale repulsivo
DU
r0
-
+
potenziale attrattivo
-U
Energia (eV)
+
-
+1.43 Fase III
0
La coppia ionica Na+Cl- è stabile ed
occorrono 4.69 eV per dissociarla
in Na e Cl.
Na++Cl-
-4.69
Na+Cl
-4.69
Fase I,II
-6.12
Na+Clr0=2.36Å
Energia reticolare nei cristalli ionici
Z1Z2e2
U=-A r
; A>1
0
(per NaCl: A=1.75)
Regola dell’ottetto nel legame ionico
Na=1s22s22p63s1
Na+=1s22s22p6
ottetto (conf. Ne)
Cl=1s22s22p63s23p5 Cl-=1s22s22p63s23p6 ottetto (conf. Ar)
Mg=1s22s22p63s2
Mg+2=1s22s22p6
ottetto (conf. Ne)
O=1s22s22p4
O-2=1s22s22p6
ottetto (conf. Ne)
Mn=(Ar)3d54s2
Mn+2=(Ar)3d5
conf. d5 (↑↑↑↑↑)
Fe=(Ar)3d64s2
Fe+3=(Ar)3d5
conf. d5 (↑↑↑↑↑)
Legame Covalente
F
E
D
C
B
U (eV)
spin paralleli
distanza r
F E D C
B
A
spin antiparalleli
A
Legame Covalente
Interazioni attrattive
Interazioni repulsive
Per l’elettrone : mvr = costante.
Se r aumenta, v diminuisce e
quindi l’energia cinetica
dell’elettrone diminuisce.
Attrazione elettrostatica
Per l’elettrone : mvr = costante.
Se r diminuisce, v aumenta e
quindi l’energia cinetica
dell’elettrone aumenta.
Per r<r0, si sviluppano interazioni
elettrostatiche repulsive fra i nuclei
Legame Covalente
Risulta da elettroni messi in comune da due atomi
Se ciascun atomo mette 1 elettrone
Legame semplice
Se ciascun atomo mette 2 elettroni
Legame doppio
Se ciascun atomo mette 3 elettroni
Legame triplo
Ordine di legame : metà del no. totale di elettroni messi in comune
H:H
ordine di legame : 2/2=1
legame semplice
O::O
ordine di legame : 4/2=2
legame doppio
N:::N
ordine di legame : 6/2=3
legame triplo
Gli elettroni che formano il legame devono avere spin antiparallelo
Attraverso la formazione di legami, gli atomi tendono a conseguire
una configurazione stabile (ottetto, d5, etc.)
Esistono due tipi di legami covalenti: s e p.
Teoria del Legame di Valenza-Legami s e legami p
•
Legami s :
elettroni di
legame posti
fra i due nuclei
e lungo la loro
congiungente
•
•
•
•
•
Legame p : elettroni di legame posti fra i
due nuclei e fuori dalla loro congiungente.
Non esistono legami p senza legami s.
I legami covalenti tra atomi uguali
si dicono omopolari, quelli fra atomi
diversi si dicono eteropolari
Legame Covalente Eteropolare
Legame covalente omopolare
Il baricentro delle cariche positive coincide con quello delle cariche negative
+d -d
r
Legame covalente eteropolare
Il baricentro delle cariche positive non coincide con quello delle cariche negative
Momento dipolare : m = rd
Unità SI : coulomb • metro
Unità Debye : carica elettronica • Å
(=3.34x10-30 C • m)
-
+

Legame Covalente Eteropolare-Metodo di Pauling
H-H
F-F
H-F
H-F
energia di legame : 4.51 eV
energia di legame : 1.60 eV
energia di legame prevista (media):
(4.51+1.60)/2 = 3.06 eV
energia di legame misurata : 5.85 eV
Energia in eccesso : D = 5.85-3.06 = 2.79 eV
D dovuta alla attrazione elettrostatica
fra cariche di segno opposto
Elettronegatività : capacità di un atomo, facente parte di una molecola,
di attrarre gli elettroni di legame verso di sé (L. Pauling, 1931).
XA-XB = 0.21√D (D espresso in kcal/mole)
% carattere ionico del legame = cost (XA-XB)
Se XA-XB = 1.7 ↔ 50%; se XA-XB < 0.4 ↔ legame covalente puro
Tavola Periodica ed Elettronegatività
F
Cl
H
Br
I
Alkali Metals
Transition Metals
Other Metals
Halogens
At
Alkali Earth Metals
lantanidi
Rare Earth Metalsattinidi
Nonmetals
Noble Gases
Momento dipolare e simmetria molecolare
Regola del parallelogramma
per la somma vettoriale
m2
m1
m2
r
r
r
m2
m1
m3
m1
Molecola lineare : F←m1-Be-m1→F (m = 0)
O
Molecola angolare : m1 m1
(m > 0)
H
H
N
Molecola piramidale : m1 m1 m1 (m > 0)
H
H
H
Molecola planare :
(m = 0)
F
m1
B
m1
m1
F
F
Orbitali ibridi
La molecola BeH2 è lineare, benché :
Per ottimizzare la formazione
di legami, l’atomo centrale combina linearmente
(ibridizza) i suoi orbitali atomici in altrettanti
orbitali specializzati (orbitali ibridi).
a
b
promozione
E(eV)
y*=Ay2p+By2s
a
b
c
22orbitali
orbitalidegeneri
degeneri
ibridizzazione
Per poter dar luogo ad orbitali ibridi,
gli orbitali atomici devono avere
energie non troppo diverse.
Tipi di orbitali ibridi
180°
BeH2
BF3
120°
Tipi di orbitali ibridi
CH4
109.5°
90°
PF5
120°
Tipi di orbitali ibridi
6 orbitali ibridi
degeneri
SF6
90°
s2
p4
sp3d2
d0
geometria ottaedrica
Orbitali sp3
CH4
H
H
H
H
Orbitali sp2
C2H4
5 legami s
1 legame p
Orbitali sp
C2H2
3 legami s
2 legami p
Isomeria geometrica
F
F
F
F
Due molecole si dicono isomeri geometrici se contengono gli stessi
atomi e gli stessi legami, disposti però in modo diverso nello spazio
F
H
F
H
H
F
H
H
rotazione
H
H
F
H
Rotameri.
Facile rotazione intorno
al legame s.
Un rotamero si trasforma
facilmente nell’altro.
Risonanza o Mesomeria nella Teoria del Legame di Valenza
Nella Teoria del Legame di Valenza il legame è localizzato
fra i due atomi che forniscono gli elettroni di valenza.
H-C
H-C
O
Forma I
Realtà :
O
O-
Formule di Lewis
O H-C
OForma II
Distanza di legame :
C-O 1.43 Å
C=O 1.22 Å
Distanza di legame : C-O 1.30 Å
O
E
I
II
Realtà :
I
C-C 1.54 Å
C=C 1.39 Å
CC 1.45 Å
Ordine di legame : 1.5
Legame dativo
Legame dativo :
donatore
H3N: + BF3 → H3N:BF3
N
B
accettore
2 elettroni
H3N→BF3 o H3N+—-BF3
N
B
F-: + BF3 → BF4-
Cl-: + AlCl3 → AlCl4-
H-: + BH3 → BH4-
H+ + :NH3 → NH4+