sviluppo storico della spettroscopia:
verso la fisica dei “quanti”
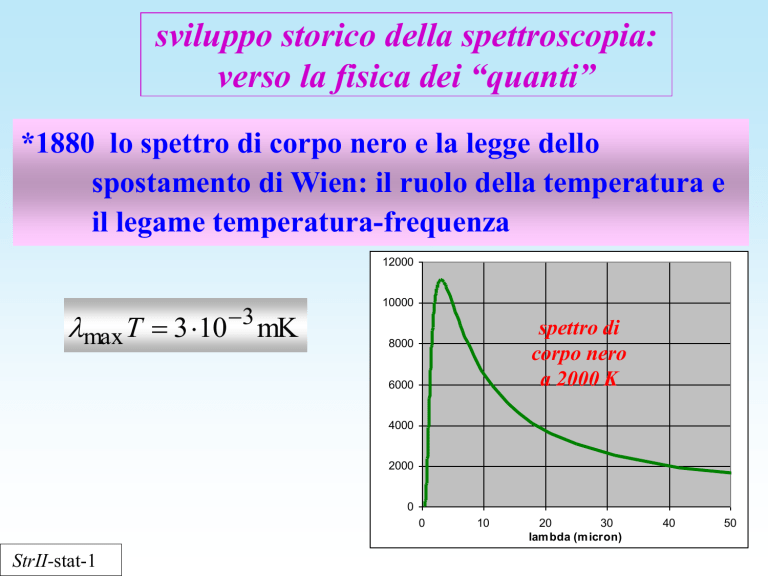
*1880 lo spettro di corpo nero e la legge dello
spostamento di Wien: il ruolo della temperatura e
il legame temperatura-frequenza
12000
max T 3 103 mK
10000
spettro di
corpo nero
a 2000 K
8000
6000
4000
2000
0
0
StrII-stat-1
10
20
30
lam bda (m icron)
40
50
sviluppo storico della spettroscopia: il “quanto di luce”
*1901 ipotesi di Planck sul “quanto di azione” h
12000
secondo
Planck
10000
8000
spettro di
corpo nero
a 2000 K
6000
secondo
Wien
4000
2000
0
0
10
20
30
lambda (micron)
40
50
* 1905 Einstein spiega l’effetto fotoelettrico, E=hf, e ipotizza il “quanto di luce”
StrII-stat-2
statistica di Boltzmann
equilibrio statistico di N particelle su n stati possibili:
• descrizione del sistema: individuare gli stati possibili (microstati),
mediante i relativi numeri quantici
• calcolare l’energia Ei dell’i-esimo stato
• calcolare la degenerazione gi dell’i-esimo stato
• calcolare la probabilità di una certa partizione, cioè in quanti modi
si possono disporre Ni particelle sugli n stati conservando l’energia totale a
disposizione (probabilità di una certa partizione di stati)
• ipotesi: tutti i microstati accessibili sono egualmente probabili
StrII-stat-3
Esempio: microstati accessibili a particelle di
massa m in una scatola cubica di lato L
1
( p x2 p 2y p z2 ) ; H ( x, y, z ) E ( x, y, z )
2m
H
statistica di Boltzmann
L
( x, y , z ) sen( k x x ) sen( k y y ) sen( k z z )
π
π
π
m x ; k y m y ; kz mz
L
L
L
1
1
2
2
3
3
2
3
1
3
1
2
3
2
3
1
2
1
6
6
E6
N6
5
E5
N5
2
2
2
1
4
E4
N4
1
1
3
1
3
1
3
1
1
3
3
E3
N3
1
2
2
2
1
2
2
2
1
3
2
E2
N2
1
1
2
1
2
1
2
1
1
3
livello energetico: Ei
1
E1
N1
1
1
1
degenerazione : gi
i
mz
gi
kx
2 2
E
( k x k 2y k z2 )
2m
E
π 2 2
2
(
m
x
2
2mL
m 2y
mz2 )
E Eo (mx2 m2y mz2 )
numeri quantici: mx my
numero di occupazione: Ni
mz
1
mx my
StrII-stat-4
statistica di Boltzmann
Esempio:
probabilità della partizione
Wi= numero di modi in cui si possono
disporre Ni particelle sul livello i
N ( N 1)( N 2)( N 3)
N!
W1
4!
N1! ( N N1 )!
W2
( N N1 )!
N
g2 2
N 2!( N N1 N 2 )!
N
gi i
W N! i
N i!
si cerca il massimo di lnW con i vincoli
sul numero totale N di particelle e
l’energia totale E (massimo vincolato):
ln W ln N ! i Ni ln gi i Ni !
i N i N
i Ni Ei E
StrII-stat-5
N1=4
N2=3
N3=5
N4=3
N5=4
N6=2
1
1
2
2
3
3
2
3
3
1
1
2
3
2
1
3
2
1
6
6
E6
N6
5
E5
N5
2
2
2
1
4
E4
N4
1
1
3
1
3
1
3
1
1
3
3
E3
N3
1
2
2
2
1
2
2
2
1
3
2
E2
N2
1
1
2
1
2
1
2
1
1
3
1
E1
N1
1
1
1
mz
gi
i
1
mx my
metodo dei “moltiplicatori di Lagrange”
Statistica di Boltzmann
formula di Stirling:
lnx! = x lnx - x
d ln Wi
dN
dNi Ei
dNi 0
i
dN
dN
dN
i
i
i
i
d ln Wi
1
ln g i (ln N i N i
1)
dN i
Ni
ln g i ln N i Ei 0 ; ln
N i Cgi e
gi
fattore di
“spazio delle fasi”
Ni
E i
gi
Ei
ha le dimensioni
dell’inverso di una energia
=1/ kBT
fBol (E,T) = e-E/kT
funzione di distribuzione
di Boltzmann
Ni Cgi f Bz ( E i , T )
StrII-stat-6
Esempio: distribuzione sui livelli
rotazionali di molecole HCl a T=300K
Statistica di
Boltzmann
Erot=Brot l(l+1) con Brot=1,3 meV
kBT=26 meV; gl=2l+1
l
gl
Erot
fBlz(Erot,T)
1,2
gl fBlz
(meV)
0
1
2
3
4
5
6
7
8
1
3
5
7
9
11
13
15
17
0
2,6
7,8
15,6
26
39
55
73
94
1
fBz
1
0,90
0,74
0,55
0,37
0,22
0,12
0,06
0,03
funzione
funzionedidipartizione
partizioneZ:
Z:
1
2,7
3,7
3,8
3,3
2,5
1,6
0,9
0,5
(Z=20)
(Z
20)
0,8
0,6
0,4
0,2
0
0
20
40
60
80
100
120
E (meV)
Z i g i f Bz ( E i , T )
probabilità di occupazione dello stato:
g i f Bz ( E i , T )
Pi
Z
StrII-stat-7
g nel caso di distribuzione “continua” di energia,
ad esempio energia cinetica E=p2/2m
spazio delle fasi
gi g(E)
cella elementare dello spazio delle fasi:
dx dy dz dpx dpy dpz = h3
numero di celle elementari con energia fra E ed E+dE:
g ( E )dE
dxdydz dp x dp y dp z
h3
g ( E )dE
V 4
2
p
dp
3
h
4V 2m3
h
per l’elettrone (due stati di spin):
3
4V 2m3
h
3
E dE
E dE
g ( E )dE
8V 2m3
h
3
E dE
StrII-stat-8
distribuzione
di Boltzmann
1.2
fBz
1
300 K
0.8
g
0.6
dNBz(E,T) = g(E) fBz(E,T) dE
0.4
dNBz(E)/dE
0.2
0
0
20
40
60
80
100
80
100
E (meV)
1.2
fBz
1
100 K
0.8
g
0.6
0.4
dNBz (E)/dE
0.2
0
0
StrII-stat-9
20
40
60
E (meV)
In quanti modi si possono disporre
2 particelle identiche in 3 celle?
P
mx= 1
my= 1
mz= 2
a
b
a
b
ab
Q
mx= 1
my= 2
mz= 1
b
a
a
b
ab
R
mx= 2
my= 1
mz= 1
StrII-stat-10
mx= 1
my= 1
mz= 2
Q
mx= 1
my= 2
mz= 1
Fermi
R
mx= 2
my= 1
mz= 1
P
mx= 1
my= 1
mz= 2
Q
mx= 1
my= 2
mz= 1
R
mx= 2
my= 1
mz= 1
b
a
b
a
ab
N
gi i
9
per Boltzmann:
Ni ! 2
indistinguibilità
classica e
quantistica
P
Bose
1
( P (a) Q (b) P (b) Q (a)) 1 (a, b)
2
1
2 (a, b) ( P (a) R (b) P (b) R (a)) 2 (a, b)
2
1
3 (a, b) ( Q (a) R (b) Q (b) R (a)) 3 (a, b)
2
4 (a, b) P (a) P (b)
1 ( a, b)
5 (a, b) Q (a) Q (b)
6 (a, b) R (a) R (b)
6 modi
1
( P (a) Q (b) P (b) Q (a))
2
1
( P (a) R (b) P (b) R (a))
2
1
( Q (a) R (b) Q (b) R (a))
2
3 modi
Statistica di
Bose - Einstein
Ni particelle in gi celle:
in quanti modi si
possono mettere gi-1
“separatori” fra le Ni
particelle
P
Q
mx= 1
my= 2
mz= 3
mx= 1
my= 3
mz= 2
R
mx= 2
my= 1
mz= 3
S
mx= 2
my= 3
mz= 1
T
mx= 3
my= 2
mz= 1
U
mx=3
my= 1
mz= 2
tutte le possibili permutazioni di Ni+gi-1 oggetti
( N g i 1)!
Wi i
N i ! ( gi 1)!
ln N i ln( N i g i 1) Ei 0
ln
Ni g i
Ei
Ni
gi
Ni E / k T
i
B 1
e
;
gi
1 e Ei
Ni
nel continuo:
dN ( E )
g ( E ) f BE ( E , T ) ;
dE
distribuzione di B.E.
g
; N i Ei
i 1
e
dN ( E )
g(E)
E / k T
B 1
dE
e
1
f BE ( E , T ) E / k T
B 1
e
funzione di distribuzione di B.E.
StrII-stat-11
Per i fotoni non c’è la conservazione
del numero totale = 0
dN ( E )
g(E)
E /k T
B 1
dE
e
gas di
fotoni
termine di spazio delle fasi per i fotoni:
g ( E )dE 2
dxdydz dp x dp y dp z
h3
due stati di polarizzazione
8πV
h3
p 2 dp
8πV
(hc)3
E 2 dE
120
100
distribuzione in energia:
dn( E )
8π
E2
dE
(hc)3 e E / k BT 1
dnBE
80
g
60
fBE
40
20
spettro di “corpo nero”
0
0
d ( )
8π
h 3
d
c 3 e h / k BT 1
50
100
150
energia (meV)
200
250
StrII-stat-12
distribuzione in energia secondo Bose (Planck):
dn( E )
1
8πE 2
1
g (E)
dE
e E / k BT 1 (hc)3 e E / k BT 1
confronto fra le
statistiche di Bose
e di Boltzmann
2
dn( E )
8
π
E
E
/
k
T
B
secondo Boltzmann (Wien):
g (E) e
e E / k BT
dE
(hc)3
120
legge di Wien dello
“spostamento”
max T 3 103 mK
fBE
100
dnBz
80
dnBE
60
legge di Wien:
d ( )
3e f ( / T )
d
g
40
fBz
20
0
legge di Rayleigh-Jeans
0
50
100
150
energia (meV)
200
250
StrII-stat-13
confronto fra le
statistiche di Bose
e di Boltzmann
12000
secondo
Planck
10000
8000
spettro di
corpo nero
a 2000 K
6000
secondo
Wien
4000
2000
0
0
10
20
30
lambda (micron)
40
50
StrII-stat-14
“temperatura di emissione spontanea
equilibrio di un
gas di fotoni”
1,2
1
E2
spettro
rotazionale di
Na Cl a 300 K
0,8
0,6
E1
i fotoni sono in
equilibrio con la
materia, cioè
scambiano in
E2 emissione stimolata
continuazione
energia con la
materia
interagendo
E1
attraverso i tre
meccanismi, di
E2
assorbimento,
emissione indotta
ed emissione
spontanea
E1
assorbimento
StrII-stat-15
0,4
0,2
0
0
20
40
60
80
100
120
E (meV)
120
100
spettro di
corpo nero
a 300 K
80
60
40
20
0
0
50
100
150
energia (meV)
200
250
equilibrio
radiazione materia
Sistema a due livelli
in condizioni di
equilibrio, le
transizioni dal livello
2 al livello 1 debbono
equilibrare le
transizioni inverse: il
numero N2 di
molecole sul livello 2
e il numero N1 di
molecole sul livello 1
deve essere costante
N2 No e
N2
E 2 / k BT
N1 N o e
E1 / k BT
A21 B21 (21)
B12 (21)
N1
E1
dN 2
( A21 B21 ( 21 )) N 2 B12 ( 21 ) N1 0
dt
emissione
spontanea
emissione
indotta
assorbimento
N2
B12 ( 21 )
e ( E2 E1 ) / k BT
N1 A21 B21 ( 21 )
(21 )
A21 / B12
e 21 / k BT B21 / B12
spettro di corpo nero se B21 = B12
StrII-stat-16
E2
energia della radiazione
ed energia della materia
N2
E2
B12 (21)
A21 B21 (21)
N1
Energia della materia:
N1E1 + N2E2
Einstein: equilibrio
statistico nella materia
Planck: equilibrio
statistico nella radiazione
E1
Energia della radiazione:
(21)
(21 )
A21 / B12
e 21 / k BT B21 / B12
( )
8π
h 3
c 3 e h / k BT 1
emissione
spontanea
dal confronto
emissione
indotta
StrII-stat-17
A21 8h 3
B21
A21
21 / k BT
;
1
;
e
1
3
B12
B12
B12 (21 )
c
dipendenza dalla temperatura del bilancio fra
energia della radiazione ed energia della materia