Prova scritta dell`esame di TEORIA DEI SEGNALI

Prova scritta dell’esame di TEORIA DEI SEGNALI
20/04/02
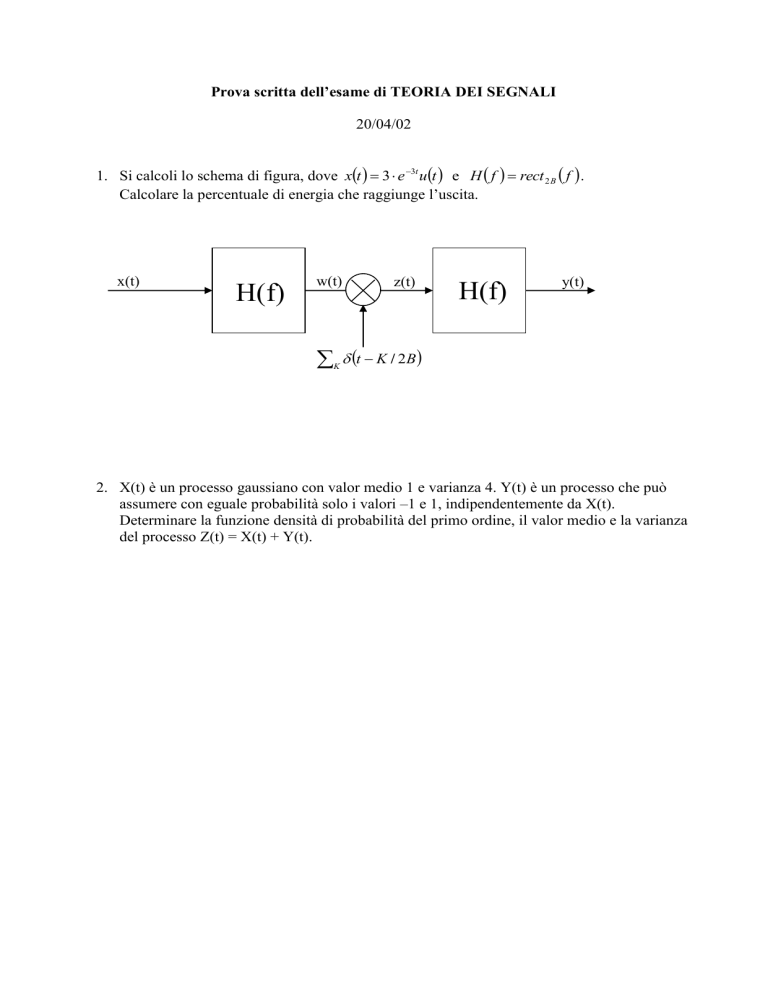
1. Si calcoli lo schema di figura, dove xt   3  e 3t ut  e H  f   rect 2 B  f  .
Calcolare la percentuale di energia che raggiunge l’uscita.
x(t)
H(f)
w(t)
z(t)
H(f)
y(t)
  t  K / 2B
K
2. X(t) è un processo gaussiano con valor medio 1 e varianza 4. Y(t) è un processo che può
assumere con eguale probabilità solo i valori –1 e 1, indipendentemente da X(t).
Determinare la funzione densità di probabilità del primo ordine, il valor medio e la varianza
del processo Z(t) = X(t) + Y(t).
1° Esercizio

Ex 
 xt 

2
dt 

Xf 

9e
0
3
3  j 2f
;
6t
e   e 0 9
dt  9

6
6
W  f H  f  
3
rect 2 B  f 
3  j 2f
Il segnale w(t) in uscita al primo filtro passa basso è un segnale passa basso con banda B.
z(t) è il segnale w(t) campionato da un treno di impulsi a frequenza 2B (frequenza di
campionamento = frequenza di Nyquist quindi no esiste l’effetto aliasing)
Z  f   W  f   2 B    f  K 2 B   2 B W  f  K 2 B 
K
K
Z(f) è pari alla ripetizione dello spettro di W(f) per frequenze multiple di 2B a meno di un fattore di
scala 2B a moltiplicare
Ne segue che il secondo filtro passa basso con banda B fa passare solo la repliche fondamentale
cioè per K=0 :
Y  f   H  f Z  f   2 BW  f   2 B

Ey 


p
Ey
Ex
S yy  f df 



Y  f  df 
3
rect 2 B  f 
3  j 2f
B

B
4B 2
9
9  4 2 f
2
df
2° Esercizio
X(t) gaussiano con media 1 e varianza 4. Poiché i parametri media e varianza sono costanti allora il
processo X(t) è stazionario.
Poiché Y(t) è un processo discretocce assume 1 e –1
f Y  y, t   p1 t   y  1  p1 t   y  1
dove p1 t   p 1 t  
1
segue che il processo Y(t) è stazionario almeno di ordine 1
2
f Y  y, t   f Y  y 
f X x 
fY y
1
2
1
Z t   X t   Y t 
1
x
1
y
X e Y s.i.
1
1
1
1

f Z z , t   f X z   f Y z   f X z     z  1   z  1  f X z  1  f X z  1  f Z z 
2
2
2
2

stazionari o almeno di ordine 1
f Z z 
1
2
EZ t   EX t   EY t   1  0  0
oppure per la simmetria della f.d.p. intorno all' asse z  1
 z   x2   y2  4  1
2
 y2  EY 2 t  0   i 2 PY t   i   1
z