Prova scritta di Misure Elettriche del 5 giugno 2013 (MECC)
1. (5 punti) Dopo aver illustrato la storia e l’importanza tecnica e commerciale del Sistema
Internazionale di unità di misura, indicare la grandezza che oggi si riesce a misurare meglio, e
perché, descrivendo sommariamente come si realizza un campione primario e i suoi principali
utilizzi. Dopo aver illustrato l’importanza delle unità logaritmiche convertire in dBm i seguenti
valori di potenza: (a) potenza elettrica di una lampadina da 100 W (b) Potenza meccanica di un
motore da 20 kW (c) Potenza termica di una reazione chimica da 5 W.
2. (5 punti) Si ha a disposizione un voltmetro numerico del tipo potenziometrico, con le seguenti
caratteristiche:
fondo scala: 10V; risoluzione 1 mV
Determinare schema a blocchi, funzionamento e cause di incertezza nel caso in cui si misuri una
tensione continua di 3V nominali. Illustrare e commentare la relazione ingresso-uscita di un ADC
ideale.
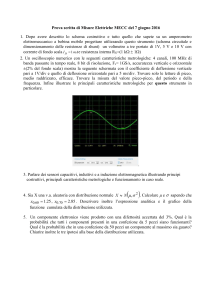
3. (6 punti) Un oscilloscopio numerico con le seguenti caratteristiche metrologiche: 4 canali, 100
MHz di banda passante, 8 bit di risoluzione, Fc= 1GS/s, accuratezza verticale (2% del fondo
scala), accuratezza orizzontale (0.003% valore letto + 50 ns ), mostra la seguente schermata:
Trovare la lettura del valore medio raddrizzato, di picco, efficace. Trovare la misura del valore
picco-picco, del periodo e della frequenza. Dopo aver disegnato e illustrato lo schema a blocchi
del solo canale verticale fare un esempio pratico per ognuna delle prime quattro caratteristiche
metrologiche che ne illustri il significato soprattutto in relazione ai blocchi appena trattati.
4. (7 punti) Si sa che il numero di chiamate telefoniche che arrivano a un centralino durante ogni
periodo di 10 minuti è distribuito come una v.a. di Poisson con =2. Dopo aver trovato valor
medio e varianza:
(a) Si calcoli la probabilità che più di tre chiamate arrivino in un periodo di 10 minuti.
(b) Si calcoli la probabilità che nessuna chiamata arrivi in un periodo di 20 minuti.
5. (7 punti) Una variabile aleatoria X continua si dice di Laplace se la sua funzione densità di
probabilità è pari a :
f X x k e
x
0,
x
Si valuti k. Dopo aver disegnato tale densità e ricavato e disegnato la funzione di distribuzione,
si determini il valor medio e la varianza di X.