COMPITO DI MATEMATICA – CLASSE 3B – Fasci di rette

COMPITO DI MATEMATICA – CLASSE 3B – Fasci di rette
Dato il fascio di rette k  1x  k  2y  k  5  0
a. Individua le rette generatrici e stabilisci se si tratta di fascio proprio o improprio
Eseguiamo le moltiplicazioni:
Raccogliamo k:
kx  x  ky  2 y  k  5  0
k x  y  1  x  2 y  5  0
Le due generatrici sono le rette:
x  y  1  0

x  2 y  5  0
Che come si può notare non hanno lo stesso coefficiente angolare, dunque non sono parallele, e
quindi il fascio è proprio.
b. Se il fascio è proprio individua le coordinate del punto C, centro del fascio
Risolviamo il sistema delle due generatrici:
x  y  1  0

x  2 y  5  0
x   y  1
x   y  1


 y  1  2 y  5  0  y  6  0
 x  6  1  7

y  6
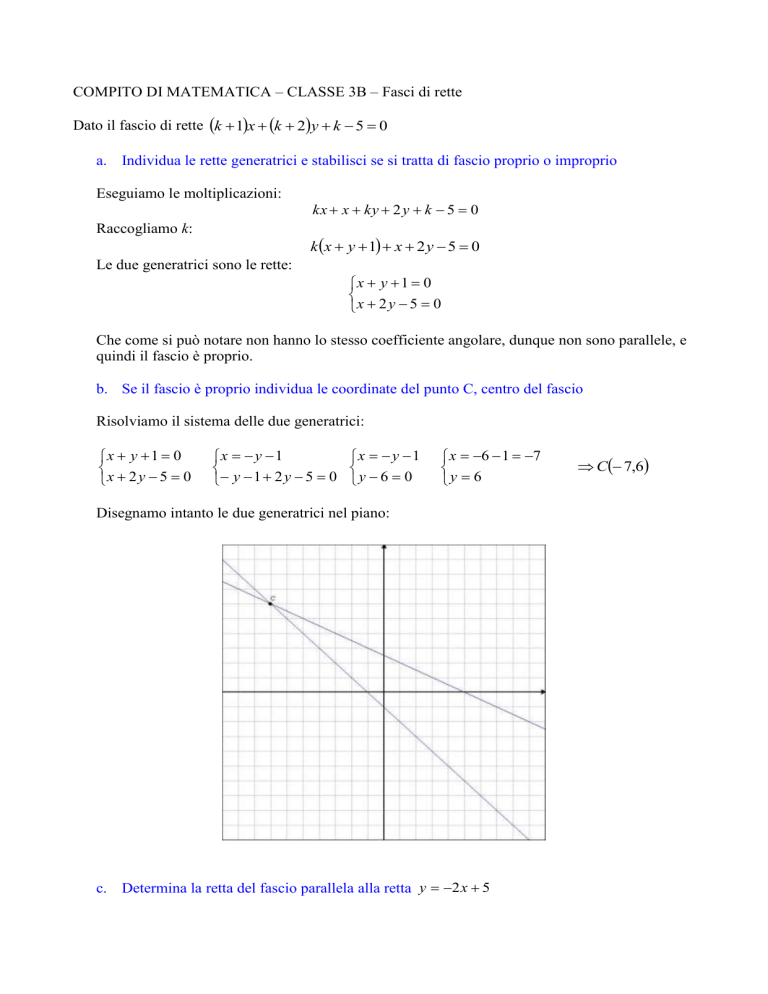
Disegnamo intanto le due generatrici nel piano:
c. Determina la retta del fascio parallela alla retta y  2 x  5
 C 7,6
Ci sono vari metodi.
I metodo: Ricaviamo il coefficiente angolare del fascio m  
Per la condizione di parallelismo dovrà essere m  2 , quindi

k 1
k 1
 2
2
k2
k2
k  1 2k  2 

k2
k2
a
k 1

con k  2
b
k2
k  1  2k  4
k  3
trovato questo valore per k si sostituisce nell’equazione del fascio e si ottiene:
 3x  y  1  x  2 y  5  0 e, svolgendo i calcoli, otteniamo y  2 x  8
II metodo: osserviamo che stiamo cercando la retta del fascio di coefficiente angolare
m  2 . Ricordando l’equazione del fascio di rette noto il centro, cioè y  y 0  mx  x0  ,
basterà sostituire il valore di m e le coordinate del centro C, per ottenere:
y  6  2x  7 , da cui, facendo i calcoli otteniamo la retta y  2 x  8
Disegnamo anche la retta trovata
d. Determina le rette del fascio parallele agli assi
Le due rette cercate devono avere equazioni del tipo:
ya
xb
(la parallela all’asse x)
(la parallela all’asse y)
dovendo entrambe le rette passare dal centro del fascio i due valore di a e b devono coincidere
con le coordinate del centro stesso, dunque:
y  6 e x  7 sono le due rette cercate. Aggiungiamole nel grafico:
Aggiungiamo anche queste due rette al disegno:
e. Determina la retta del fascio passante per l’origine
I metodo: sfruttiamo la condizione di appartenenza punto – retta e sostituiamo le coordinate
dell’origine nell’equazione del fascio. Otteniamo:
k  1  0  k  2  0  k  5  0
Sostituiamo il valore di k trovato
nell’equazione del fascio e otteniamo:
5x  y  1  x  2 y  5  0 e,
svolgendo i calcoli, otteniamo
6
y x
7
II metodo: osserviamo che se la retta
passa per l’origine il suo termine noto
deve essere nullo, dunque:
k 5
0
k 5  0
k 5
k2
e con gli stessi passaggi otteniamo la
6
retta y   x
7
Aggiungiamo la retta nel disegno:
k 5  0
k 5
f.
Determina la retta del fascio passante per A2,2
Procediamo come nel primo metodo
del caso precedente e sostituiamo le
coordinate del punto nell’equazione del
fascio:
k  1  2  k  2  2  k  5  0
svolgendo i calcoli otteniamo:
2k  2  2k  4  k  5  0
1
k
5k  1  0
5
e sostituendo nell’equazione del fascio,
abbiamo:
1
x  y  1  x  2 y  5  0 da cui
5
otteniamo la retta 4 x  9 y  26  0
Aggiungiamola nel grafico:

1
g. Determina la retta del fascio perpendicolare alla retta y   x  6
3
Il procedimento è analogo a quello del
punto c. Con la condizione di
perpendicolarità anziché di
parallelismo, ossia m  3 , essendo
1
 il coefficiente angolare della retta
3
data.
Utilizziamo il secondo metodo, per
rapidità.
y  6  3x  7 y  3 x  27
Utilizzando il primo metodo avremmo
7
trovato il valore di k ( k   ), che
4
sostituito nell’equazione del fascio ci
avrebbe dato, con qualche calcolo in
più la retta cercata.
Aggiungiamo anche questa retta nel
grafico:
h. Determina l’area del triangolo di vertici ABC, essendo B il punto di intersezione della retta
di cui al punto c con l’asse delle ascisse
Per prima cosa troviamo le coordinate di B, intersecando la retta y  2 x  8 con l’asse delle x.
Risolviamo il sistema
y  0

 y  2 x  8
y  0
y  0


 2 x  8  0  x  4
B 4,0
Rappresentiamo nel grafico il triangolo
di cui vogliamo calcolare l’area.
Scegliamo come base il segmento AC e
come altezza il segmento BH, e
calcoliamone la lunghezza. Per AC, si
tratterà di calcolare la distanza tra due
punti:
AC 
2  72  2  62
 97
Per BH, dobbiamo invece usare la
distanza punto – retta, nello specifico del
punto B dalla retta 4 x  9 y  26  0 :
BH 
4   4  9  0  26

 16  26

42
97
97
42  92
Possiamo infine calcolare l’area del triangolo:
A
1
42
 97 
 21
2
97
e questo è tutto!